Глобальний і локальний оптимуми

 

При відшуканні оптимуму цільової функції R(U) задачею, як правило, є визначення сукупності значень незалежних змінних U_j, що відповідає не якому-небудь екстремуму функції R(U), а найбільшому чи найменшому значенню R(U_j) у припустимої області Vдоп. Якщо шукається, наприклад, мінімум, то рішення задачі оптимізації повинне задовольняти умові:

 

R(U_опт) < R(U) (5.12)

 

причому U Î V. Умова (5.12) повинна виконуватися для будь-яких припустимих значень U.

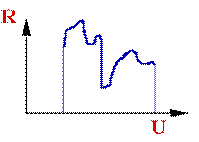
Оптимум, для якого справедливо умова (5.12), звичайно називається глобальним. Крім нього функція R(U) може мати один чи трохи локальних екстремумов (рис.5.9). У цьому випадку складність задачі пошуку екстремума для функції багатьох перемінних значно збільшується.

 

 

Рис.5.9

Методи рішення задач оптимізації

Вибір методу рішення - один з найважливіших етапів оптимізації.

Можна виділити наступні групи методів:

- аналітичні методи;

- методи математичного програмування.

Розглянемо більш докладно групи цих методів і деякі з них.

Група аналітичних методів оптимізації поєднує аналітичний пошук екстремуму функції, метод множників Лагранжа, вариаційні методи і принцип максимуму.

Аналітичний пошук екстремуму функції, заданих без обмежень на незалежні перемінні, застосовується до задач, у яких оптимізуєма функція має аналітичне вираження, що диференцується у всьому діапазоні дослідження, а число перемінних невелике. Це один з найбільш простих методів.

Група методів математичного програмування включає динамичнє програмування, лінійне програмування і нелінійне програмування.

Динамічне програмування - ефективний метод рішення задач оптимізації багатостадійних процесів. Метод припускає розбивку аналізованого процесу на стадії (в часі чи в просторі)- наприклад, реактор у каскаді чи тарілка в колоні. Розгляд задачі починається з останньої стадії процесу й оптимальний режим

визначається постадійно.

Лінійне програмування - метод для рішення задач оптимізації з лінійними вираженнями для критерію оптимальності і лінійними обмеженнями на область зміни перемінних. Подібні задачі зважуються ітераційними способами. Ці методи використовуються при оптимальному плануванні виробництва при обмеженій кількості ресурсів, для транспортних задач і ін.

Методи нелінійного програмування- поєднують різні способи рішення оптимальних задач: градієнтні, безградієнтні і випадкового пошуку. Загальним для методів нелінійного програмування є те, що їх використовують при рішенні задач з нелінійними критеріями оптимальності. Усі методи нелінійного програмування - це чисельні методи пошукового типу. Суть їх - у визначенні набору незалежних перемінних, що дають найбільше збільшення оптимізуємої

функції. Дана група методів застосовується як для детерминованіх, так і стохастичних процесів.

Аналітичні засоби

Аналітичні засоби засновані на класичних засобах математичного аналізу. Задача оптимізації формулюється наступним чином. Існує процес, відома його математична модель та встановлений критерій оптимізації R у вигляді функції:

(5.13)

або функціонала:

, (5.14)

де .

Задані обмеження:

та . (5.15)

Необхідно при заданих обмеженнях знайти такі значення , при яких R досягає екстремуму. У випадку функціонала R необхідно знайти вид функції ,при якої R досягає екстремуму.

Аналітичні засоби пошуку екстремуму критерію оптимальності застосовуються до задач, у яких оптимiзуєма функція має аналітичний вираз, а число перемінних невелике. У вигляді прикладу розглянемо визначення оптимального часу перебування суміші у РІВ.

Для двох послідовних реакцій необхідно визначити оптимальний час перебування t, при якому вихід целевого продукту В буде досягати максимуму.

Нехай а - початкова концентрація компоненту А. В початковий момент часу концентрації компонентів В та D дорівнюють нулю: при t = 0: C_B = С_D = 0. Критерій оптимізації: вихід цільового продукту . Керуючий вплив - час перебування t. Характер зміни концентрацій компонентів в часу приведений на рис 5. 10.

Нехай реакції протікають по першому порядку.

Швидкість реакцій

 

(5.16)

 

(5.17)

 

(5.18)

 

Із (5.16) знайдемо вираз для поточної концентрації С_А.

;

Проiнтегрiровав, одержимо:

 

(5.19).

 

Рис. 5. 10

Підставимо (5.19) та (5.17) в (5.18):

,

або

. (5.20)

Розв'язав одержане рівняння, знайдемо вираз для визначення поточної концентрації компонента В:

. (5.21)

 

Вихід цільового продукту R=C_B/a = . (5. 22)

 

Дослідимо екстремум одержаної цільової функції (5.22). Умови існування максимуму: <0.

Знайдемо першу похідну і прирівняємо її нулю:

. (5.23)

 

Вирішив одержане рівняння, визначимо оптимальний час перебування:

 

. (5.24)

 

Для перевірки виконання достатньої умови існування максимуму обчислюємо другу похідну:

 

Так як друга похідна менш 0, отже у наданій точці існує максимум цільової функції R.

Підставив (5.24) у (5.21), одержимо вираз для визначення максимальної концентрації компонента В:

. (5.25)