
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод покоординатного спуска Гаусса - ЗейделяСодержание книги
Поиск на нашем сайте
Наданий спосіб по суті аналогічен методу релаксації. Відміна укладається лише в тому, що у наданому методі не визначається осьовий напрям, вдовж якої цільова функція змінюється найбільш сильно, а по черзі змінюються всі незалежні перемінні так, щоб по кожної з них досягалося екстремальне значення цільової функції. Як і у методі релаксації, кожна уточнюва перемінна варіюється до тих пор, поки на наданому осьовому напрямі не буде знайдений екстремум. Після цього починається кроковий пошук по наступному осьовому напрямку. Стратегія пошуку точки екстремуму по напрямку може бути будь-якою, в тому числі можна використовувати будь-який з методів одномірного пошуку. Очевидно, що оскільки варіювання незалежних перемінних діється у встановленому порядку, метод покоординатного спуска приводить до оптимуму більш довгим шляхом. Проте, загальний обсяг обчислювань у порівнянні з методом релаксації може опинитися меншим, так як. при переході до уточнення значення наступної перемінної похильні цільової функції не обчислюються. Основним достоїнством наданого методу є його простота. До недоліків треба віднести труднощі пошуку точки екстремуму при наявності обмежень та " байраків ", а також, аналогічно методу релаксації, неможливість визначення глобального екстремуму. При використанні методу покоординатного спуска для визначення екстремуму по напрямку звичайно застосовує один з наступних алгоритмів – пошук з постійним кроком або пошук з перемінним кроком. Суть першого алгоритму укладається у слідкуючому. Кроки у обраному напрямку здійснюються до отих пор, поки цільова функція буде змінюватися у необхідну сторону, наприклад, зменшуватися в разі пошуку мінімуму. Як тільки ця умова порушується, т. є. точка екстремуму по напрямку пройдена, робиться один крок у зворотному напрямку. І ця точка вважається точкою екстремуму по наданому напрямку. Найкращі результати дає використання другого алгоритму. Він відрізняється від першого отим, що після переходу через точку екстремуму змінюється не тільки знак кроку пошуку, але і його величина - наприклад, зменшується в два рази. Наданий алгоритм дозволяє точніше визначати стан екстремуму по напрямку, що у кінцевому підсумку дозволяє скоротити загальне число обчислювань для знаходження екстремуму цільової функції.
Метод Хука - Джiвса
Наданий метод пошуку точки екстремуму цільової функції є більш ефективним у порівнянні з методом покоординатного спуска. Пошук складається з послідовності кроків пошуку, що досліджується навколо базисної точки, за яким в разі успіху треба пошук по зразку. Алгоритм методу наступний. 1. Вибирається початкова базисна точка B1 і крок hj для кожної перемінної Xj (j=1, 2,..., n). Можна використовувати й однаковий крок h для всіх перемінних. 2. Пошук, що досліджує, проводиться з метою одержання зведень про локальне поводження цільової функції в окрузі базисної точки. Ці зведення надалі будуть використані для перебування напрямку пошуку за зразком. 2.1. Обчислюється значення цільової функції R(B1) у базисній точці. 2.2. Кожну незалежну перемінну по черзі змінюємо на розмір кроку. Таким чином, обчислюється значення цільової функції R(B1 +h1 e1 ), де e1 - одиничний вектор у напрямку осі x1. Якщо це призводить до зменшення значення цільової функції (в випадку пошуку минимума), то B1 змінюють на B1 +h1 e1. У противному випадку обчислюється значення функції R(B1 -h1e1) і якщо її значення зменшилося, те B1 заміняють на B1 -h1 e1. Якщо жодний із пророблених кроків не призводить до зменшення значення цільової функції, то точка B1 залишається незмінної і розглядаються зміни в напрямку осі x2, тобто знаходять значення функції R(B1 +h2 e2) і т.д. Коли будуть розглянуті усе n перемінних, то одержимо нову базисну точку B2. 2.3. Якщо B2 =B1, тобто зменшення функції не було досягнуто, те дослідження повторюється навколо тієї ж базисної точки B1, але зі зменшеним розміром кроку. На практику задовільним рахується зменшення розміру кроку (кроків) у десять разів від початкової довжини. 2.4. Якщо B2 ≠ B1, те провадиться пошук за зразком. 3. При пошуку за зразком використовується інформація, отримана в процесі дослідження, і мінімізація функції завершується пошуком у напрямку, заданому зразком. 3.1. Розумно рухатися з базисної точки B2 у напрямку B2 -B1, оскільки пошук у цьому напрямку вже призвів до зменшення значення цільової функції. Точка зразка може бути обчислена в такий спосіб:
P1 = B1 +2*(B2 - B1) (5.57)
У загальному випадку:
Pi = Bi +2*(Bi+1 - Bi) (5.58)
3.2. Проводиться дослідження в округах точки P1(Pi). 3.3. Якщо найменше значення на кроку 3.2 менше значення в базисній точці B2 (у загальному випадку Bi+1), те одержують нову базисну точку B3 (Bi+2), після чого варто повторити крок 3.1. У противному випадку не провадиться пошук за зразком, а заміняється базисна точка. У якості нової базисної точки вибирається та точка, у якому на попередньому кроку значення цільової функції було мінімальним. Потім виконується дослідження навколо нової базисної точки. 4. Процес пошуку завершується, коли довжина кроку (довжини кроків) стануть менше заданого малого значення.
Метод сканiрованiя
Наданий метод укладає у послідовному перегляді значень цільової функції у ряді точок, що належать до області зміни незалежних перемінних, та знаходженні серед цих точок такої, у якій цільова функція має екстремум. Точність методу, природно, визначається отим, наскільки густо розташуються обрані точки у галузі пошуку. Основним достоїнством методу сканiрованiя є оте, що при його використанні з достатньо " густим " розміщенням точок завжди гарантується відшукування глобального екстремуму. Проте, для цього у наданому методі вимагається чималий обсяг обчислювань. Метод сканiрованiя не пов'язаний з наявністю локальних екстремумів на відміну від практично всіх інших методів нелінійного програмування. Тому його можна використовувати для грубої оцінки " областей притяжіння " локальних екстремумів, після чого можуть застосовуватися методами градiєнтного пошуку для точного визначення координат кожного екстремуму. Найбільш простий алгоритм пошуку екстремуму методом сканiрованiя "пошук на сітці перемінних" укладається в тому, що по кожної незалежної перемінної задаються припущення у відповідному порядку, що забезпечує " заповнення" всієї досліджуваної області рівномірною та достатньо густою сіткою. Так, наприклад, для пошуку екстремуму функції двох перемінних спершу при фіксованому значенні Uk2 розраховуються значення R(Uj) при UK1 = UK-11 для всього діапазону зміни незалежної перемінної Uj та фіксує значення екстремуму. Після цього друга перемінна змінюється на крок ΔU2 UK2= UK-12U+ΔU2 і розрахунки повторюються при варіюванні перемінної Uj Для довільного числа перемінних крок по наступної перемінної виробляється після отого, як повністю завершений цикл по попередньої. Обсяг обчислювань при використанні методу сканiрованiя можна оцінити по наступній формулі:
де Δ - точність визначення екстремума n - кількість незалежних перемінних.
Тому метод сканiрованiя ефективно використовується при числі перемінних не більш трьох. Існують різноманітні модiфикації методу сканiрованiя, що застосовуються в основному для скорочування обсягу обчислювань. Розглянемо одну з них - сканiрованiє з перемінним кроком. Спершу задається достатньо великий крок (ΔU > ) та виконується " грубий " пошук, що локалiзує область існування глобального екстремуму (P) (рiс. 5.26). Рис 5.26
Після отого, як область визначена, виробляється пошук з меншим кроком тільки в межах знайденої області. Можна організувати ряд таких процедур послідовного уточнення по положення оптимуму
При використанні наданого алгоритму обсяг обчислювань істотно але скорочує і може бути визначений по наступній формулі:
де r - число етапів уточнення пошуку, на якому крок зменшувався в К раз n - число незалежних перемінних; Δ - точність визначення екстремуму. Початковий крок сітки перемінних в даному випадку визначається формулою:
Δ o=Kr Δ (5. 59)
При n = 2, Δ = 10-3, r = 2, K = 10 и Δo = 0,1 кількість обчислювань S=900. При постійному кроці сканiрованiя для отих же умов вимагалося 106 обчислювань, т. є. обсяг обчислювань скоротився більш ніж у 1000 раз. Ще більш чималий виграш спостерігається при більшому числі незалежних перемінних. Так, для отих же наданих, але при n = 3 число обчислювань з перемінним кроком сканiрованiя складе S = 17000, а для постійного кроку S = 109.
Симплексний метод
Основна ідея цього методу укладається в тому, що по відомим значенням цільової функції у вершинах опуклого многогранника, що називається симплексом, знаходиться напрямок, у якому вимагається зробити наступний крок, щоб одержати найбільше зменшення (збільшення) значення цільової функції. При цьому під симплексом в n-мірним просторі розуміється многогранник, що має n+1 вершину. Прикладом симплекса в двомірним просторі, т. є. на площині, є трикутник. В трьохмірним просторі - тетраедр. Симплекс володіє наступною властивістю - проти будь-який з його вершин Sj розміщена тільки одна грань, на якої можна збудувати новий симплекс, що відрізняється від колишнього розміщенням нової вершини Sj тоді як інші вершини обох симплексів співпадають. Вершина нового симплекса S, взагалі кажучи, може знаходитися і по іншу сторону грані від вершини Sj. Ця властивість симплекса і обумовлювала можливість його застосування при рішенні задач оптимiзації. Розглянемо найпростіший випадок - пошук мінімуму цільової функції двох перемінних R(U1,U2). Алгоритм пошуку наступний: 1. Розраховуються значення цільової функції у вершинах обраного вами симплекса S10, S20, S30 (рис.5.27).
3. Новий симплекс S11,S20,S30 будується таким засібом: - знаходиться середина грані S20,S30, яка розташована проти вершини S10 - крапка А. Через крапки S10 і А проводиться пряма. На цій прямій від крапки А відкладається відрізок АS11, рівний по величині відрізку S 10 А. 4. У новій вершині обчислюється значення цільової функції. 5. З вершин нового симплекса S11, S20, S30 вибирається та, де значення цільової функції максимально. Рис.5.27
6. Аналогічно п.3 будується новий симплекс S11, S20, S31, тобто виключається вершина S30, що мала найбільше значення цільової функції і т.д. У результаті застосування розглянутої процедури виключення вершин симплексів з найбільшим значенням цільової функції процес пошуку сходиться до мінімального значення R(U1,U2). При виникненні зациклення в околицях крапки екстремуму необхідно зменшувати розміри симплекса. Критерієм закінчення пошуку можуть служити розміри симплекса. Наприклад, якщо всі ребра симплекса стануть менше δ, те пошук можна припиняти. Розглянемо алгоритм симплексного методу для задач довільної розмірності. Нехай вершинам вихідного симплекса Si (i=1,2,...,n+1) відповідають координати U(i) =(U(i)1,U(i)2 ,..., U(i)n), (i=1,2,...,n+1). І нехай найбільше значення цільової функції відповідає вершині Sj. Визначимо координати вершини Ŝj нового симплекса. Вершина Ŝj розташовується симетрично вершині Sj щодо середини грані, що знаходиться проти вершини Sj. Координати центра цієї грані U(i) визначаються по формулі: (5.62) причому підсумовування ведеться тільки по тим векторам U(i), що відповідають вершинам Si, що утворюють цю грань. Вектор, що характеризує відстань від вершини Sj до центра грані, яка розташована проти цієї вершини, буде:
Координати вершини Sj визначаються по формулі
Підставивши в (5.64) вираження для U з (5.62), одержимо:
Формула (5.65) визначає координати вершини Sj нового симплекса. При необхідності зменшити розміри симплекса (у випадку зациклення в околиці крапки оптимуму) замість формули (5.63) можна користатися наступним вираженням:
Найбільше ефективно симплексний метод сходиться при використанні правильних симплексів - рівностороннього чи трикутника тетраедра, утвореного рівносторонніми трикутниками. У цьому випадку напрямок пошуку збігається з напрямком градієнта (якщо симплекс досить малий). Симплексний метод володіє ще одним важливим достоїнством - при збільшенні розмірності задачі обчислювальні витрати зростають незначно, тому що на кожнім кроці вважається тільки одне значення цільової функції.
Метод Нелдера-Мида
Метод Нелдера-Мида є розвитком симплексного методу Спендли, Хекста і Химсворта. Ідея методу складається в порівнянні значень функції в n+1 вершинах симплекса і переміщенні симплекса в напрямку оптимальної крапки за допомогою ітераційної процедури. У даному методі симплекс переміщається за допомогою трьох операцій: відображення, розтягання і стиски. Зміст цих операцій стане зрозумілим при розгляді кроків процедури. А. Знайдемо значення функції у вершинах симплекса.
f1 = f(x1); f2=f(x2);.....fn+1=f(xn+1)
Б. Серед обчислених значень знайдемо найбільше значення функції fmax, що випливає за найбільшим значенням функції fcp, найменше значення функції fmin і відповідні їм крапки
Xmax, Xcp, і Xmin.
В. Знайдемо центр ваги всіх крапок, за винятком крапки Xmax (тобто середину грані, яка розташована проти крапки Xmax).
Обчислимо f(XO)=f. Г. Зручніше за все почати переміщення від крапки Хmax. Відбивши крапку Хmax щодо крапки Хо, одержимо крапку Хr і знайдемо f(Хr) = f. Якщо α - коефіцієнт відображення, то положення крапки Xr визначається в такий спосіб:
Хr - Хо = α.(Хо - Хmax) чи Хr = (1 + α) Хо - α.Хmax,
де α = │ Хr - Хо│∕│ Хо - Хmax│
Д. Порівняємо значення функцій f і fmin. 1. Якщо f < fmin, то в знайденій крапці одержали найменше значення функції. Напрямок із крапки Хо в крапку Хr найбільше доцільно для переміщення. Тому, ми робимо розтягання в цьому напрямку і знаходимо крапку Хe і значення функції f = f(Xe). Коефіцієнт розтягання γ > 1 можна знайти з наступних співвідношень:
Xe - Xo = γ (Xr - Xo), тобто Xe = γ. Xr + (1 - γ) Xo,
де γ = │Xe - Xo│ / │Xr - Xo│.
а) Якщо f < fmin, те заміняємо крапку Xmax на крапку XE і перевіряємо (n + 1)- ую крапку симплекса на збіжність до мінімуму (див. крок 3). Якщо збіжність досягнута, то процес зупиняється; у противному випадку повертаємося на крок Б. б) Якщо f > fmin, те відкидаємо крапку XE. Очевидно, ми перемістилися занадто далеко від крапки Xo до крапки Xr. Тому варто замінити крапку Xmax на крапку Xr, у якій було отримане поліпшення (крок Д, 1), перевірити збіжність і, якщо вона не досягнута, повернутися на крок В. 2. Якщо f > fmin, але f ≤ fcp, те Xr є кращою крапкою в порівнянні з іншими двома крапками симплекса і ми заміняємо крапку Xmax на крапку Xr і, якщо збіжність не досягнута, повертаємося на крок Б. 3. Якщо f > fmin, і f > fcp, то перейдемо на крок Е. Е. Порівняємо значення функцій f і fmax. 1. Якщо f > fmax, то переходимо безпосередньо до кроку стиску Е,2. Якщо f < fmax, то заміняємо крапку Xmax на крапку Xr і значення функції fmax на значення функції f. Запам'ятовуємо значення f > fcp із кроку Д.2, приведеного вище. Потім переходимо на крок Е, 2. 2. Так як у цьому випадку f > fmax, тому ясно, що ми перемістилися занадто далеко від крапки Xmax до крапки Xo. Спробуємо виправити це, знайшовши крапку Xc ( а потім f) c допомогою кроку стиску. Якщо f > fmax, то відразу переходимо до кроку стиску і знаходимо крапку Xc зі співвідношення Xc - Xo = β (Xmax - Xo),
де (0 < β < 1) - коефіцієнт стиску. Тоді Xc = β. Xmax + (1 - β) Xo. Якщо f < fmax, то спочатку замінимо крапку Xmax на крапку Xr, потім зробимо стиск. Тоді крапку Xc знайдемо зі співвідношення
Xc - Xo = β (Xr - Xo),
тобто Xc = β Xr + (1 - β) Xo (Рис. 4).
Ж. Порівняємо значення функцій f і fmax. 1.Якщо f < fmax, то заміняємо крапку Xmax на Xc, і якщо збіжність не досягнута, то повертаємося на крок Б. 2.Якщо f > fmax, то очевидно, що всі наші спроби знайти значення менше fmax закінчилися невдачею, тому ми переходимо на крок З. З. На цьому кроці ми зменшуємо розмірність симплекса розподілом навпіл відстані від кожної крапки симплекса до Xmin - крапки визначальної найменше значення функції. Таким чином, крапка Xi заміняється на крапку Xi + 1/2(Xi-Xmin), тобто заміняємо крапку Xi крапкою 1/2(Xi-Xmin). Потім обчислюємо fi для i = 1,2,..., (n + 1), перевіряємо збіжність і, якщо вона не досягнута, повертаємося на крок В. И. Перевірка збіжності заснована на тім, щоб стандартне відхилення (n + 1) -го значення функції було менше деякого заданого малого значення ε. У цьому випадку обчислюється
де
Якщо σ < ε, те всі значення функції дуже близький друг до друга і тому вони, можливо, лежать поблизу крапки мінімуму функції Xmin. Тому такий критерій збіжності є розумним. Коефіцієнти α, β і γ є відповідно коефіцієнтами відображення, стиски і розтягання. Автори рекомендують брати α=1; β = 0.5; γ = 2. Початковий симплекс вибирається довільно. Методи випадкового пошуку Основна ідея методів випадкового пошуку полягає в тім, що перебором випадкових сукупностей значень незалежних перемінних знайти оптимум цільової чи функції напрямок руху до нього. Існує значна кількість методів випадкового пошуку, з яких будуть розглянуті лише найбільш розповсюджені. Загальним для всіх методів випадкового пошуку є застосування випадкових чисел у процесі пошуку. Розглянемо лише основні поняття про випадкові числа. Під випадковою величиною розуміють величину, що приймає в результаті іспитів значення, що принципово не можна пророчити, виходячи з умов досвіду. Випадкова величина має цілий набір припустимих значень, але в результаті кожного окремого досвіду приймає лише якесь одне з них. Випадковий вектор, визначений у n-мірному просторі α = (α1, α2,..., αn) може з рівною імовірністю приймати будь-як напрямок у n-мірному просторі і має довжину, рівну 1. Такий вектор може бути отриманий з послідовності випадкових чисел βj (j = 1, 2,..., n), рівномірно розподілених на інтервалі [-b, b]. Для перебування випадкового вектора a за допомогою послідовності випадкових чисел β, виразимо компоненти випадкового вектора αj наступними співвідношеннями:
(5.67)
Вектор α, компоненти якого розраховуються по (5.67), характеризує випадковий напрямок у n-мірному просторі. Випадкова крапка. Під випадковим вибором деякої крапки в заданій області простору розуміється випадковий вибір з імовірністю влучення в задану околицю будь-якої крапки зазначеної області, рівної відношенню обсягу околиці крапки до обсягу всієї області. Координати випадкової крапки знаходяться за допомогою випадкових чисел βj, заданих на інтервалі [-b, b]. Нехай область простору нормованих перемінних Uj (j = 1, 2,..., n) задана умовами: 0 < Uj < 1 (j = 1, 2,...,n) (5.68)
Для визначення координат випадкової крапки можна використовувати наступні співвідношення:
Xj = (bj +b)/ (2.b) (j = 1, 2,... n) (5.69)
Деякі способи одержання випадкових чисел будуть розглянуті нижче. До числа найбільш розповсюджених методів випадкового пошуку відносяться метод сліпого пошуку, метод випадкових напрямків і його модифікації.
Метод сліпого пошуку
При використанні сліпого пошуку в припустимій області зміни незалежних перемінних випадковим образом вибирається крапка, у якій обчислюється значення цільової функції. Далі, аналогічно вибирається інша випадкова крапка, де також розраховується значення цільової функції і порівнюється з отриманим раніше. Якщо значення цільової функції в новій крапці виявляється меншим, чим у попередній крапці (у випадку пошуку мінімуму), то нове значення запам'ятовується разом з координатами крапки, для якої воно було обчислено. Потім продовжується вибірка випадкових крапок і порівняння значень цільової функції в цих крапках із уже знайденим. Щораз, коли знаходиться менше значення цільової функції, воно запам'ятовується з відповідними значеннями координат, після чого продовжується пошук кращого наближення до крапки екстремуму. Пошук закінчується, якщо після виконання наступної серії з S кроків менше значення цільової функції знайти не удалося. Теоретично при застосуванні такої стратегії і досить великому числі іспитів можна досягти як завгодно високого ступеня точності у визначенні положення крапки оптимуму. Але на практиці використання методу сліпого пошуку істотно обмежується розмірністю розв'язуваної задачі і складністю обчислення цільової функції. Так, наприклад, навіть при n=2 і з імовірністю P =0.5 для того, щоб положення крапки оптимуму визначити з точністю? = 0,001 необхідно виконати не менш S виборів випадкових крапок. Число виборів S можна оцінити по формулі (5.70)
З (5.70) видно, що число необхідних обчислень різко збільшується зі зростанням розмірності розв'язуваної задачі. Аналогічно методу сканування, можна після грубого наближення до крапки оптимуму проводити пошук вже в більш вузькій області, що приведе до скорочення обсягу обчислень.
Метод випадкових напрямків
Алгоритм цього методу полягає в тім, що з крапки n-мірного простору, для якої цільова функція розрахована, виробляється крок у випадковому напрямку, обумовленому випадковим вектором α(k). Величина кроку задається параметром h. У результаті знаходиться наступна крапка
U(k+1) = U(k) + h.α(k) (5.71)
У новій крапці обчислюється значення цільової функції. Якщо при виконанні випадкового кроку h.α(k), що приводить у крапку U(k+1), виходить менше значення цільової функції, то крок вважається вдалим (у випадку пошуку мінімуму) і нове значення цільовий функції запам'ятовується разом з координатами крапки U(k+1) Потім робиться новий h.α(k+1) у випадковому напрямку і т.д. Якщо випадковий крок h.α(k) виявляється невдалим, то продовжується вибірка наступного випадкового вектора α і з крапки U(k) знову виконується крок. Спробні кроки з крапки U(k) робляться доти, поки не буде знайдена крапка U(k+1), у якій цільова функція буде мати менше значення. Потім спробні кроки виконуються з крапки U(k+1). Пошук закінчується, якщо після виконання серії з S кроків меншого значення цільової функції знайти не удалося. Можна використовувати цей алгоритм, застосовуючи крок h(k) змінної величини. При цьому ефективність методу трохи зростає за рахунок застосування більш великого кроку удалині від крапки оптимуму. У цьому випадку після виконання серії з S невдалих кроків пошук не закінчують, а зменшують величину кроку h(k) і проводять нову серію обчислень. Критерієм закінчення пошуку служить мінімальний розмір кроку hmin, яким і задається точність визначення екстремуму.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.237.52 (0.013 с.) |

 (5.59)
(5.59) При n = 2 та Δ = 10 кількість обчислювань S = 10-6, а при тому ж значенні точності n = 3 S = 10-6.
При n = 2 та Δ = 10 кількість обчислювань S = 10-6, а при тому ж значенні точності n = 3 S = 10-6. (5.60)
(5.60)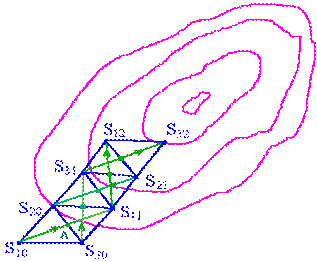 2. Вибирається вершина, де значення R(U1,U2) найбільше - S10.
2. Вибирається вершина, де значення R(U1,U2) найбільше - S10.





 .
.


