
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Побудова Q - T -діаграми і дослідження стійкості стаціонарних режимів РІЗСодержание книги
Поиск на нашем сайте
Однією із основних характеристик хімічного реактора є його стійкість,тобто спроможність вертатися до вихідного стаціонарного стану після усунення зовнішніх збуреннь. Для дослідження стійкості РІЗ широко використовують діаграму залежності тепловиделення і тепловідводу від температури (Q-T діаграму). Спершу розглянемо залежність швидкості реакції, яка протікає в РІЗ, на прикладі єдиної необоротної реакції 1-го порядку. Швидкість реакції в розмірному виді виражається наступною залежністю: W = K × C = K0 × e –E/RT × C (2.12)
де t = V/Q - час контакту,c. Підставляя (2.13) в (2.12),остаточно одержимо:
Графік залежності (2.14) має наступний вид (див. рис.2.2):
Рис 2.2
При малих значеннях температури T другий доданок в знаменнику зневажливо малий по зрівнянню з одиницею.Тоді:
В цій області з підвищенням температури швидкість реакції зростає по закону Аррейнiуса(нижня вітка графіка). При великих температурах,навпаки, другий доданок в знаменнику формули (2.14) стає набагато більше одиниці.Тоді: W0=C0 t (2.16) де t = V/Q - час контакту. Фізичний зміст залежності (2.16) достатньо зрозуміло. При високих температурах реакція протікає настільки хутко, що реагує практично вся речовина,що надходить в апарат.В цьому режимі швидкість реакції W практично не залежить від температури (верхня вітка графіку). Аналогічний вид мають ці залежності і в безрозмірної формі. Для побудови Q-T-діаграми розглянемо рівнення енергетичного балансу в безрозмірної формі (2.10). В стаціонарному режимі накопичування тепла дорівнює нулю. Запишемо рівнення енергетичного балансу у наступному виді:
Позначимо ліву частину порівняння qR-виділення тепла,тобто кількість тепла,що виділяється при протечі хімічної реакції в одиницю часу, а праву – qT-отвод тепла,тобто кількість тепла, що отводиться через стінку холодильника із струмом. В стаціонарному режимі виділення і отвод тепла дорівнюються між собю qR = qT. Перетворюємо вираз для розрахунку величини теплоотводу q:
Остаточно:
де a = QBX + gQX. Вираз для розрахунку величини тепловиділення qR:
Характер залежностей (2.18) і (2.19) від температури наступний вираз (2.18) становить порівняння прямої лінії, причому q зростає, коли збільшується q.У виразі (2.19) DQАД - коеффiциєнт,який не залежить від температури, так що залежність qR від q має такий вид, як функція W = f (T) (рівняння 2.14), відрізняясь лише масштабом (рис. 2.3).
Як видно із графіку (рис.2.3) в наданій сітуаці при одніх і отих же значеннях вхідних параметрів можливі три різноманітних стаціонарних режима, що забезпечують не тільки значення різноманітних вихідних параметрів, але і відрізняються по стійкостi. Рис.2.3.
Розглянемо спершу стаціонарний режим 3, що відповідає режиму роботи при температурі q3. Так як швидкості виділення і отвода тепла однакові, оте поки температура q не зміниться, режим залишається стаціонарним. Припустимо, що внаслідок випадкового обурення змінюється значення x і відбувається зміщення на величину Dq. При цьому за рахунок прискорення швидкості реакції зростає швидкість виділення тепла; це зростання діється по лінії, яка відповідає кривої тепловиділення. Одночасно, за рахунок збільшення різниці температур між температурами в реакторі і теплоносія зростає швидкість відведення тепла, це зростання діється по лінії тепловідводу. В крапці 3 лінія тепловідвода минає з більш великим кутом наклона,чим лінія тепловиділення. Тому при температурі q3 + Dq швидкість відвода виявляється вищою,ніж швидкість його виділення. В цих умовах, після зняття обурення Dq реактор почне охолоджуватися. Охолодження буде тривати до отих пор, поки температура в реакторі не стане дорівняної q3. При цій температурі швидкості від вода і виділення тепла знову зрівняються і режим знов стане стаціонарним. Навпаки, якщо внаслідок обурення (q = q – Dq) реактор почне охолоджуватися, оте після зняття обурення (тому що швидкість виділення тепла при цих умовах перевищує швидкість тепловідводу) реактор знову почне нагріватися до досягнення в ньому температури, яка дорівнює q3.
Таким чином, стаціонарний режим в крапці 3 вертається до вихідного стану після зняття зовнішніх обурень, можна сказати що режим стійкий. Спроможність системи (реактора) вертатися до вихідного стаціонарного стану після зняття обурень називається стійкiстью. Інакше кажучи, вихідний стаціонарний режим є стійким, якщо після усунення джерел порушення режиму будь-які малі відхилення з течією часу прагнуть до нуля. Якщо ж значення відхилень наростають в часу, оте вихідний стаціонарний режим нестійкій. При температурі q1, відповідній стаціонарному режиму 1, з погляду стійкiстi картина повністю аналогична розглянутому вище режиму в крапці 3, тому що і в цьому випадку лінія тепловідвода іде круче, чим лінія тепловиділення і вихідний стаціонарний режим стійкий. Тепер розглянемо режим в крапці 2. Тут наклон лінії тепловідвода менш, чим лінії тепловиділення. Але також, як і в крапках 1 і 3, qR = qT і якщо немає обурень, режим буде стаціонарним. Хай сталося випадкове обурення і температура q1 підвищілася на величину Dq. При температурі q = q + Dq швидкість виділення тепла стає більше, ніж швидкість тепловідвода. І тому після зняття обурення реактор буде не охолоджуватися,а нагріватися, віддаляясь від вихідного стану. Нагрів буде тривати до отих пор, поки знов швидкість тепловиділення не буде дорівняної швидкості тепловідвода, т. є. реактор досягне нового стаціонарного стану - при температурі q3. Аналогічно, при заперечливих обуреннях реактор буде самопроiзвольно охолоджуватися до отих пор,поки не досягне стійкого стаціонарного стану при температурі q. Проведений аналіз показав, що із трьох можливих в наданих умовах стаціонарних режимів тільки два:1- при низькій температурі і, відповідно, малої швидкості реакції) і 3-при високій температурі і великої швидкості реакції є стійкимi, а третій - при проміжних значеннях температури і швидкості реакції (крапка 2) - нестійкий. Умова стійкостi Умова стійкостi визначається співвідношенням тепловідвода і тепловиділення. Режими є стійкими, якщо швидкість тепловідвода перевищує швидкість тепловиділення. Враховуючи геометричний зміст похильной умову стійкістi можна сформулювати наступним образом система стійка,якщо кут наклона крiвой тепловиділення менш, чим лінії тепловідвода
2.1.6 Вплив вхідних параметрів на стаціонарні режими. Розглянемо вплив зміни основних параметрів на вході в РІЗ на стаціонарні режими. Швидкість тепловідвода є функцією наступних параметрів: qT = f(qвх ; qх; g) (2.21)
Розглянемо вплив температури входу на стаціонарні режими. При збільшенні qвх лінія тепловідводу буде зміщатися праворуч. При цьому умови існування стаціонарних режимів будуть іншими. На рис.2.4 показані лінії тепловідтводу, збудовані при різних значеннях q.
Рис 2.4
Рис2.5 При більш великих значеннях qвх лінія тепловідвода лежить нижче лінії тепловиділення практично у всієї області,за винятком високих значень q. В даному випадку має місце тільки один стаціонарний режим – точка 9. Аналогічна картина спостерігається і при зменшенні значення q. Розглянемо докладно стаціонарні режими в крапках 7 і 13.Малійша зміна температури приводить до того, що реактор практично миттєво переходить на високотемпературний режим (із точці 7 в точку 8 на верхньої ветвi графіку) або, навпаки, на спідкотемпературний режим (із точки 13 в точку 14 на нижньої ветвi). Аналіз роботи реактора слушно проводити з використанням статичних характеристік, що показують зміну вихідних величин (в даному випадку - q) в стаціонарному режимі при зміні параметрів на вході. Кількісною мірою зміни вихідних величин при зміні вхідних параметров служить параметрична чутливiсть - межа відношення зміни вихідної величини до відповідної зміни вхідной:
де A - вхідний параметр. Вирыз (2.22) є ніщо інше, як: P = dq/dA (2.23) На практиці звичайно використають слідуючий близький вираз: P» Dq/DA (2.24) Статична характеристика при зміні qвх приведена на рис.2.5.Для побудови статичної характеристики використаються тільки крапки стаціонарних режимів, одержаних при побудові Q-Т діаграми при зміні температури входу. Для кожного значення температури входа вибираються крапки, відповідні стаціонарним режимам і переносяться на графік статичної характеристики. Позначимо m-основний робочий режим. Розглянемо iнтервал qвх` – qвх``. В цьому діапазоні температур можливо існування трьох режимів.У разі, коли qвх > qвх`` або qвх < qвх` в реакторі буде тільки один стійкий режим (високо або низкотемпературний). Із статичної характеристики також видно, що вдалині від крапок 7 і 13 (що називаються крапками зриву) величина параметричної чутливостi невелика. По мірі наближення до цих крапок величина параметричної чутливостi різко зростає, а після цього діється скачкообразний перехід на інший режим - зрив. В крапках зриву величина P нескінченно велика. В ході нормальної експлуатації реактора завжди мають місце невеликі вагання вхідних параметрів. В зв'язку з цим виникає завдання визначення запасу стійкостi сукупності допустимих відхилень параметрів процесу. Практично запас стійкостi становить iнтервал від заданого режиму до кордону стійких стаціонарних станів. Так, наприклад, для режиму m запас стійкостi по температурі входу складає:
Dqвх = qвх7 – qвхm Для забезпечення стійкої і безпечної роботи реактора необхідно виконання наступного обмеження: Dqвх > dqвх де Dqвх - можливий iнтервал зміни q в процесі експлуатації Розглянемо вплив параметра g на стаціонарні режими в РІЗ. З порівняння (2.18) виходить, що параметр g визначає наклон лінії тепловідвода. Із збільшенням величини g кут наклона буде зростати, а лінія тепловідвода буде повертатися навкруг деякої точки (рис.2.6). Визначимо коордiнати цієї крапки. Для цього розглянемо два випадки: g1 = 0 і g2 = 1. В цьому випадку, величина тепловідвода буде равна: qТ1 = q – qВХ і qТ2 = 2 × q – qвх – qХ. Оскільки ця точка - "центр обертання" є загальною для обох випадків, оте у неї qТ1 = qТ2. Тоді: q – qВХ = 2q – qВХ – qХ . Звідси q = qХ - абсциса центру обертання.
Рис 2.6 Ордiната наданої крапки - qТ = qХ – qВХ. Статична характеристика РІЗ по каналу q – g приведена на рис. 2.7.
Рис 2.7
При малих значеннях g існує єдиний високотемпературний режим - область а. По мірі збільшення g спостерігається перехід в область існування трьох режимів - область b. При великих значеннях g буде існувати єдиний нiзкотемпературний режим - область с. При певних значеннях параметра g можливі “зриви” із високотемпературного режиму на нiзкотемпературний – точка 13 і навпаки – точка 7. Порівнявши статичні характеристики q = f(qвх) і q=f(g) можна спостерегти, що вони є зеркальним відбиванням друг друга. Розглянемо вплив величини адiабатичного розігріва на характер стаціонарних режимів в РІЗ. Величина адiабатичного розігріва для однієї і отієї ж реакції є функцією тільки концентрації на вході в реактор – С0. При зміні Dqад змінюється положення лінії тепловиділення - qp (рис.2.8).
Рис 2.8 Із зменшенням величини адаiбатичного розігріва графік залежності qR = f(q) зменьшується по висоті і зміщується праворуч.В крапці 13 діється зрив на нiзкотемпературний режим. При збільшенні Dqад картина змінюється. Графік залежності зміщується ліворуч, збільшуясь по висоті, і в крапці 7 переходить скачкообразно на високотемпературний режим. Статична характеристика по каналу q – DqАД (рис.2.9) має такий же вигляд,як і статична характеристика по каналу q - qВХ. Аналогічним образом будуються статичнi характеристики при варіюванні інших параметрів.
Рис 2.9
Необхідно визначити наступне.Вище були розглянуті випадки, коли можливе існування в реакторі деяких стаціонарних режимів. В тому випадку, якщо існує єдиний стаціонарний режим, оте вид статичних характеристик змінюється. Побудова статичних характеристик проводиться наступним чином. Вибирається вихідний стаціонарний режим. Після цього при варіюванні одного із вхідних параметрів визначаються нові стаціонарні режими. Статичнi характеристики будуються, як правило,в коордiнатах Dqвих = f (DaВХ), де аВХ -параметр на вході (рiс. 2.10).
Рис 2.10
Дослідження статичних характеристик в будь-якому реакторі необхідно, поперше, для провiщування поводження об'єкту при зміні умов на вході; подруге, для вибору канала управління, тобто отакого параметра, яким можна варіювати, щоб здійснювати процес в заданих умовах при можливих флуктуаціях вхідних параметрів.
При виборі каналу управління необхідно, щоб: 1. Зміна параметра на вході виявляла помітний вплив на вихідні параметри. 2. Обраний канал управління повинен бути найменьш iнерційним,тобто часу, протягом якого параметр на виході відреагує на зміну вхідного параметра,слід бути мінімально можливим. Реактор ідеального витиснення (РІВ) Характерною особливістю РІВ є те,що в ньому не діеться змішення вдовж напряму руху потоку.У будь-якому поперечному перетині реактора частки мають однакову швидкість руху. Математична модель РІВ Якщо у РІВ параметри змінюються по довжині реактора, то для висновку рівнянь балансів виділяється елементарниий обсяг шару висотою dZ.
L - довжина реактора, м; Z - відстань від входу до вибранного шару висотою dz, м; S - перетин реактора,м2; U - швидкість струму (м/с); Q = U × S (м 3 /с)- об'ємний видаток; V = S×dz- обсяг виділеного елементарного шару,м3; Свх,Твх - концентрація і температура на вході в шар; C, Т - концентрація і температура на вході у виділений шар; W - швидкість хімічного перетворення; Рис 2.11
Складемо порівняння матеріального балансу для виділеного елементарного прошарку за одиницю часу dt.
В рівнянні (2.25) перше слагаєме враховує кількість речовини, що вноситься із струмом у виділений елементарний обсяг прошарку; друге-кількість речовини,що виноситься з потоком; третя- кількість речовини, яка витрачається (образується) внаслідок хімічного перетворення. Права частина враховує зміну кількості речовини у виділеному елементарному прошарку.Перетворив (2.25), одержимо остаточний вигляд дорівнення матеріального балансу для РІВ:
Енергетичний баланс складається аналогічно.
Тут перший та другий доданок враховують прихід і видаток тепла з конв'єктивним струмом у виділений елементарний об'єм; третій - тепловіділення за рахунок хімічної реакції, четвертий-відвід(підвід) тепла з теплоносiєм. Права частина - накопичення тепла. Вважаючи, що СP і r - незмінні у всьому обсязі реактора і спростивши цю залежність,одержимо остаточний вигляд енергетичого балансу для РІВ:
Рівняня кiнетикi. В загальному випадку швидкість хімічного перетворення висловлються наступною залежністю: W=F( де C -вектор концентрації {С1, C2.... Cn }. В математичну модель РІВ входять кордонні і початкові умови, а також обмеження. Кордонні умови для РІВ - умови протікання процесу на вході в прошарок. Z = 0 C = CBX T = TBX (2.30) Початкові умови встановлюють значення концентрації і температури у реакторі в початковий момент часу. t = 0 C = CBX T = TBX (2.31) Обмеження: Tmin < T < Tmax Cmin < C < Cmax (2.32)
Система порівнянь (2.26) - (2.32) становить математичний опис РІВ в розмірній формі.При описі стаціонарних режимів в зрівняннях балансів проiзводні по часу прирівнюються нулю. Дослідження РІВ.
|
|||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 265; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.0.200 (0.015 с.) |

 Значення концентрації C в реакторі залежить від величини концентрації на вході C0 і температури в реакторі T. Із рівнення матеріального балансу для стаціонарного режиму (2.7) слідує, що C = C0/(1+Kt) = C0/(1+K0 × e–E/RT × t) (2.13)
Значення концентрації C в реакторі залежить від величини концентрації на вході C0 і температури в реакторі T. Із рівнення матеріального балансу для стаціонарного режиму (2.7) слідує, що C = C0/(1+Kt) = C0/(1+K0 × e–E/RT × t) (2.13)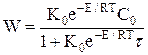 (2.14)
(2.14) (2.15)
(2.15)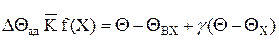 (2.17)
(2.17)
 (2.18)
(2.18)
 Лінії залежностей qR і qT від температури пересікаються в трьох крапках - 1, 2 і 3. В цих крапках при температурах q1, q2, q3 процес стаціонарен, тому що дотримується умова стаціонарностi qR = qT або b × dq/dt' = 0.
Лінії залежностей qR і qT від температури пересікаються в трьох крапках - 1, 2 і 3. В цих крапках при температурах q1, q2, q3 процес стаціонарен, тому що дотримується умова стаціонарностi qR = qT або b × dq/dt' = 0. (2.20)
(2.20)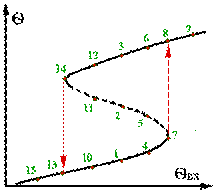 Оскільки порівняння залежності швидкості тепловідвода від параметрів (2.18) подає порівняння прямої лінії, оте при зміні параметрів,які входять в коефіціент a - qвх і qх, лінія тепловідвода буде переміщатися паралельно самої собі.
Оскільки порівняння залежності швидкості тепловідвода від параметрів (2.18) подає порівняння прямої лінії, оте при зміні параметрів,які входять в коефіціент a - qвх і qх, лінія тепловідвода буде переміщатися паралельно самої собі. Стаціонарні режими,одержані при базовому значенні qвх, позначені цифрами 1,2,3. При збільшенні qвх лінія тепловідводу зміщується праворуч.При цьому число стаціонарних режимів залишається колишнiм (позначені 4,5,6). При подальшому збільшенні qвх число стаціонарних режимів спромагається змінитися. Для деякого значення qвх одержуємо тільки два стаціонарних режима – точки 7 та 8, причому стаціонарний режим в крапці 7 -нестійкій.
Стаціонарні режими,одержані при базовому значенні qвх, позначені цифрами 1,2,3. При збільшенні qвх лінія тепловідводу зміщується праворуч.При цьому число стаціонарних режимів залишається колишнiм (позначені 4,5,6). При подальшому збільшенні qвх число стаціонарних режимів спромагається змінитися. Для деякого значення qвх одержуємо тільки два стаціонарних режима – точки 7 та 8, причому стаціонарний режим в крапці 7 -нестійкій.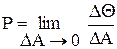 (2.22)
(2.22)



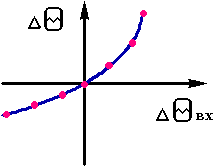
 Запровадемо наступні позначення:
Запровадемо наступні позначення: (2.25)
(2.25)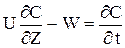 (2.26)
(2.26)
 (2.27)
(2.27)
 (2.28)
(2.28) × T) (2.29)
× T) (2.29)


