
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделювання процесу на одному зерні каталiзатораСодержание книги
Поиск на нашем сайте
У всякому гетерогенному процесі взаємодія між компонентами діється на поверхнi розділу фаз чи в безпосередньоу близькості від неї. Тому сучасні каталiзатори становлять порiсті матеріали з високорозвиненою внутрішньою поверхністью. Головна причина, що змушує застосовувати подібні каталiзатори це багаторазове збільшення поверхнi розділу фаз. Так, якщо непорiста гранула діаметром 5 мм має поверхність порядку 10-4 м2, то поверхність пор в порiстої гранулі такого ж розміру може складати 20-600 м2, т.ч. різниця може досягати 105 раз. Картина процесу, протекающого в порiстом зерні каталiзатора відрізняється великою складністю, тому що діфузія речовини проходить в вузьких порах, форма і перетин яких непостоянні. Для аналізу процесів в зерні каталiзатора була запропонована достатньо проста схема - квазiгомогенная модель. Відповідно до цього зерно розглядається не як складна система пор, а як деяке суцільне непоруш-не середовище, всередині якого іде дифузія реагентів (обумовлена ефективним коефіціентом дифузії
Рис 3.4 При зроблених допущеннях iзотермичеський процес в зерні каталiзатора описується рівнянням:
(3.1)
де С - поточна концентрація; e - порiстость зерна каталiзатора; r - поточна коордiната; t - час; D - ефективний коефіціент дiффузii; W -швидкість хімічного перетворення; Краєві умови: прі r = 0 C = Cп (3. 2) прі r →∞ C → 0 Для реакції 1-го порядку W=K SУд Wс (3. 3) де К-константа швидкості реакції, віднесена до одиниці поверхнi; Sуд - питома поверхня, рівна відношенні суммарноу поверхні до обсягу зерна.
Для опису стаціонарного режиму при проходженні реакції першого порядку дорівнення (3.1) прийме слідуючий вигляд:
(3.4)
Вираз (3.4) з урахуванням краєвих умов (3.2), одержимо
(3.5)
Позначимо:
Тоді, замість (3.5) можна записати:
Формула (3. 7) у безмірному вигляді виражає глибину проникнення реагента в зерно каталiзатора. На рис. 3.5 зображений графік цієї формули. По мірі углублення в зерно каталiзатора концентрація зменшуеться. Теоретично Практично це вірно, починаючи з r/l ≈5 при цьому відношення концен трацій C/c ≈ 0, 01, і, відповідно швидкість реакції на два порядка менша, чим у зовнішньоу поверхнi.
Рис.3.5.
Для аналізу впливу різноманітних факторів на хід реакції слушно аналізува ти протікання процесу, прийнявши за абсцису або r, або аналізувати протікання або відношення r/d, де d -діаметр зерна каталiзатора. В цьому випадку розподіл концентрацій по зерну нескінченних розмірів, а певного діаметру d. Виявляється, що розподіл концентрацій істотно залежить від відношення L/d. Взагалі кажучи,параметр L можна трактувати як масштаб глибини проникання реагента в зерно каталiзатора. З іншого боку, цей параметр можна трактувати як деяку міру співвідношення швидкості дифузії і реакції: при малому значенні швидкість дифузії значно менш швидкості реакції та навпаки.В літературі широко використовується слідуючий параметр, назад пропорційний параметру L- безмірний модуль Тiле:
де R - радіус зерна. Модуль Тiле визначає відношення швидкості реакції до швидкості дифузії. Залежно від величини параметра j можливі різноманітні режими роботи каталiзатора. 1. При малих значеннях модуля Тiле (ψ <0. 5) швидкість хімічної реакції значноменш, чим швидкість дифузії. В цьому випадку центру зерна буде відповідати дуже малі значення відношення r/l. Із ріс. 3.7 видно, що при цьому концентрація реагента в центрі зерна буде така ж, як і на поверхнi, т. ч. С ≈ Сп обсяг каталiзатора працює з однаковою інтенсивністю, а швидкість процесу на зерні буде визначатись хімічною реакцією. Профіль концентрації по діаметру зерна показаний на рис. 3.6 (верхня крива), цю область роботи каталiзатора прийнято називати кiнетичною т. ч. лiмiтiрующей стадією є кiнетика процесу.
Рис 3.6
Однією з найважливіших характеристик процесу на порiстому зерні каталiзаора є ступінь використання внутрішньої поверхнi каталiзатора,рівна відношенню спостерігаємоу швидкості реакції до швидкості реакції у відсутністі внутрi дiффузiонного гальмування, у кiнетичнiй області: h=Wнабл / Wкин (3.9) Для кінетичної області (при значеннях ψ < 0,5) міра використання близька до 1, тобто використовуеться практично вся внутрішня поверхня. З зростанням модуля Тiле величина міри використання η монотонно прагне до нуля і у галузі значень ψ > 2, 5 процес протікає в внутрiдiффузiонноу області.В цьому випадку η =1/ ψ, тобто чим більше ψ, отим менш η. Між діфузійною і кiнетичною областями лежить перехідна область, відповідаюча умовам, при яких концентрація реагента в центрі зерна каталiзатора менш, ніж на зовнішній поверхнi, але вище розрахованной по рівненню (3.5). В цій області з зростанням параметру ψ міра використання змінюється від значень, характерних для кiнетичноу області, до значень, характерних для дифузійної області. У перехідній області працюють багато промислові каталiзатори. На графіку залежності міри використання внутрішньої поверхнi від параметра Тiле (рiс. 3.7) чітко вiдни ці три області протікання процесса на зерні: - відтинок АB (j <0,5)-кінетична;
- відтинок BC - перехідна область. Змищенню процесу з дифузійної в перехідну сприяють зменшення розміру зерна R збільшення ефектив коефіціенту діфузії D. Останнє в значно визначається збільшенням діаметрів пор. Щоб за рахунок такого зростання не надто зменшити внутрішню поверхню зерна каталiзатора, доцільно застосовувати Рис 3.7 каталiзатори з бiдiсперсною структурою - широкі транспортні пори та дрібні мікропори. Таким чином, знаючи швидкість переносу реагентів всередині зерна каталiзатора, можна зробити попередні висновки про його оптимальні порiсті структури. Дамо визначення оптимальної структури. Швидкість реакції W, віднесена до одиниці обсягу зерна каталiзатора, - це по суті активність одиниці обсягу каталiзатора. Вона залежить від питомої активності WУд – скоростi реакції, віднесеної до одиниці поверхнi каталiзатора, питомої повехностi каталiзатора SУД і її доступності, що характеризується мірою використання внутрішньої поверхні h W=Wуд * Sуд * h (3.10) Для наданого хімічного складу каталiзатора його питома активність приблизно постійна. Отже, максимальна активність каталiзатора відповідає максимальному значенню SУД*h. Порiсту структуру, що забезпечує цю умову, прийнято називати оптимальною. Надане визначення відноситься до нагоди протікання простих реакцій. Для складних реакцій оптимальна порiста структура повинна забезпечувати максимальну швидкість реакції при заданої селектівностi. Для реакцій, протікающіх у кiнетичній області, швидкість реакції прямо пропорційна загальної внутрішньої поверхнi (h = 1).Максимальне значення твору
SУД*h можливо при тонкопорiстої структурі зерна каталiзатора. Для реакцій, протікающих в діффузійній області, міра використання менш 1, що пояснюється впливом внутрiдiффузiйнного гальмування Максимальне значення твору SУД*h у данному випадку залежить не тільки від величини внутрішньої поверхнi, але і від параметра ψ. При інших рівних параметрах зменшити величину ψ i відповідно, збільшити h можна за рахунок зменшення розміру зерна. При цьому відкриваються нові устья пор, в яких протікає реакція. При подальшому роздрібненні наступить такий стан, коли в усіх порах концентрація С стане рівної Сп і процес перейде в кiнетичну область. Основні рекомендації по вибору оптимальної порiстої структури повинні засновуватися на аналізі впливу процесів переносу речовини всередині зерна і хімічного перетворення, а також обліку технологічних умов здійснення конкретного процесу. Помiмо оптимальної порiстой структури на показники роботи реактора істотний вплив оказують розміри зерна каталiзатора і його форма. Під оптимальними формами і розмірами зерен каталiзатора будем розуміти такі, що дозволяють досягнути задану проiзводiтельность при мінімальних видатках на контактний апарат з каталiзатором і подолання його гідравлічного опору. Теоретична оптимiзація.
На рис. 3.8 приведені ці залежності для нагоди протекання необоротної реакції для трьох значень часу контакту,причому t1 > t2 > t3. З зростанням температури збільшується константа швидкості реакції, відповідно, швидкість хімічноного перетворення. По мірі протечи реакціі зменшується конценрація, що у кінці прагне до 0, тому що Х → 1. Вихід продукту при цьому максималєн. Із рис. 3.8 також видно, що збільшення часу контакту в реакторі дозволяє при заданій температурі забезпечити понад високу міру перетворення. На рис. 3.9 приведені аналогічні залежності для випадку протечи оборотної реакції. В цьому випадку для кожного значення часу контакту при підвищенні темпе ратури спершу спостерігається зростання міри перетворення до деякого максимального значення, а після цього - зниження. Температура, яка відповідає максимальному виходу продукта називається оптимальною темпера турою.
ідеального витиснення. Состав продуктів на виході із реактора залежить від профіля температури в самому реакторі. Очевидно, що повинен існувати такий температурний профіль, при якому вихід цільового продукту буде максимальним. Для простих процесів (з однією хімічною реакцією) визначення оптимальних умов упрощаєтся. Ці процеси є незв'язними, для них оптимальний режим не залежить від протечи процесу в інші моменти часу. Інакше кажучи, локальная швидкість хімічного процесу повинна бути максимальною в кожний момент часу чи в кожному перетині реактора. Розглянемо деякі випадки, коли можна вказати характер оптимального температурного профіля. Якщо ріст температури, пришвидчучи процес, збільшує селектівність (або не впливає на неї), оте оптимальна температура повинна бути максимально високою. Так, підвищення температури:
При протеканiї хімічних реакцій іншого типу для визначення оптимального температурного режиму використовуються різноманітні засоби рішення завдань оптимізації. У вигляді прикладу розглянемо знаходження оптимального температурного профіля для оборотної екзотермічної реакції А В + Q причому енергія активації прямої реакції менш, що зворотної, тобто E1 > E2. В цьому випадку підвищення температури прискорює зворотну реакцію сильніше, чим пряму, так що рівновага процесу зміщувається в небажану сторону. При деякій температурі швидкість утворення цільового продукту проходить крізь максімум. ця оптимальна температура залежить від составу реакційної суміші, зміншуясь по мірі зниження концентрації вихідної речовини рис. 3.9. Таким чином, спершу, поки що не накопичилася кількість кінцевого продукту, процес вигідно вести при високій температурі, щоб збільшити швидкість прямої реакції, а після цього температуру треба знижувати, щоб змістив рівновагу в потрібну сторону, добитися максимального виходу цільового продукту. Температура в кожному перетині реактора повинна бути обрана так, щоб швидкість утворення цільового продукту в цьому перетині була максимальною, щоб викону валася рівність dr/dt = 0 (умова існування екстремума функції). Якщо температурна залежність константи швидкості реакції визначається рівняннєм Аррейнiуса, оте рівняння швидкості реакції має наступний вигляд:
(3.17)
де K01, K02 - предекспоненціальні множителi прямої та зворотної реакцій. E1, E2 - енергії активації прямої та зворотної реакцій* f (C), v(C) - кiнетичні функції прямої та зворотної реакцій, відбиті через концентрацію одного із початкових речовин, що приймається заключеве. Дiференціруя (3.17) по температурі та приравняв похідну до нулю, одержимо вираз для визначення оптимальної температури процесу як функцію концентрації ключевого компоненту:
(3.18)
Підставив в (3.18) відповідні значення концентрації ключевого компоненту чи міри перетворення, можна одержати оптимальний температурний профіль. Аналогічні залежності одержані і для інших типів реакцій. Оптимальний температурний режим для найбільш поширених типів реакцій зображено на рис. 3.10
Для паралельних реакцій у випадку, коли енергія активації побіної реакції більше, чим основної E1 > E2, оптимальний температурний профіль відповідає лінії 3. Розглянуті вище приклади відносяться до випадку, коли керуючим параметром служить температура. В інших випадках для мети управління можна використовувати тиснення, состав реакційної суміші та ін. Необхідно також визначити, що при визначенні оптимального режиму необхідно, як правило, враховувати різноманітні обмеження - по составу газової суміші, термостійкістi каталiзатора, обсяговому видатку реакційної суміші.
|
|||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 223; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.163.26 (0.012 с.) |

 ) і в якій протікає хiмiчеська реакція (визначаєма константой швидкості реакції, віднесенноу до одиниці обсягу зерна KЗ). При цьому, якщо реакція іде при постійній температурі, то значення
) і в якій протікає хiмiчеська реакція (визначаєма константой швидкості реакції, віднесенноу до одиниці обсягу зерна KЗ). При цьому, якщо реакція іде при постійній температурі, то значення 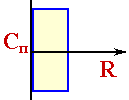 Для побудови моделі введем слідуюче спрощення - будемо розглядати зерно каталiзатора безкінцевих розмірів. При цьому дiффузіонний струм спрямований від поверхні зерна вглиб уздовж осі R на безмежну глибину (рис.3.4). Мета цього спрощення складається у отому, щоб завдання стало одномерним - розглядається тільки одна коордiната.
Для побудови моделі введем слідуюче спрощення - будемо розглядати зерно каталiзатора безкінцевих розмірів. При цьому дiффузіонний струм спрямований від поверхні зерна вглиб уздовж осі R на безмежну глибину (рис.3.4). Мета цього спрощення складається у отому, щоб завдання стало одномерним - розглядається тільки одна коордiната.

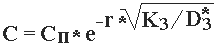
 (3.6)
(3.6) (3.7)
(3.7) зменшення може тривати до r = ∞.
зменшення може тривати до r = ∞. (3. 8)
(3. 8) 2. Більші значення ψ >2, 5 відповідають режиму, при якому швидкість реакції значно більше швидкості діфузії. При цьому проходить швидке падіння концентрації реагента і реакція завершується в гирлі пор Наданому режиму відповідає нiжня крива на ріс. 3.6 Таку область роботи каталiзатора прийнято називати внутридiффузiонною, так як лiмiтiрующа стадія всього процесу є дифузія реагента у середину зерна каталiзатора.
2. Більші значення ψ >2, 5 відповідають режиму, при якому швидкість реакції значно більше швидкості діфузії. При цьому проходить швидке падіння концентрації реагента і реакція завершується в гирлі пор Наданому режиму відповідає нiжня крива на ріс. 3.6 Таку область роботи каталiзатора прийнято називати внутридiффузiонною, так як лiмiтiрующа стадія всього процесу є дифузія реагента у середину зерна каталiзатора. - відтинок CD (j >2,5) -дiффузiонна;
- відтинок CD (j >2,5) -дiффузiонна;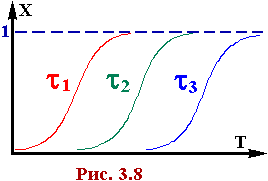 На етапі теоретичної оптимiзаціi визначається теоретичний оптимальний режим, що надалі є об'єктивним критерієм оцінки вибору конструкції реактора і всієї технологічної схеми. У вигляді прикладу розглянемо залежності міри перетворення від температури при різноманітних часах контакту для єдиної екзотермічної реакції - необоротної і оборотноЇ.
На етапі теоретичної оптимiзаціi визначається теоретичний оптимальний режим, що надалі є об'єктивним критерієм оцінки вибору конструкції реактора і всієї технологічної схеми. У вигляді прикладу розглянемо залежності міри перетворення від температури при різноманітних часах контакту для єдиної екзотермічної реакції - необоротної і оборотноЇ. Розглянемо одну із простійших задач оптимiзаціi - визначення оптимальної температури в кожному перетині реактора
Розглянемо одну із простійших задач оптимiзаціi - визначення оптимальної температури в кожному перетині реактора

 Лінія 2 визначає оптимальний температурний профільдля оборотних реакцій типу А В + Q та послідовних реакцій типу A-à Bà C, коли E1 < E2.
Лінія 2 визначає оптимальний температурний профільдля оборотних реакцій типу А В + Q та послідовних реакцій типу A-à Bà C, коли E1 < E2.


