
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методи дослідження усталеностіСодержание книги
Поиск на нашем сайте
Усталеність - одна з найважливіших характеристик матеріальних систем. Під стійкістю розуміють здатність системи зберігати свій стан в умовах впливу середовища, що обурює. Дослідження стійких і хитливих стаціонарних станів здійснюватися на основі аналізу поводження системи в часі після впливу якого-небудь збурювання. А.М.Ляпунов у 1935 році вперше дав строгу постановку задачі про усталеність руху і запропонував два методи рішення. Ці роботи стали основою вивчення стійкості технічних систем, у тому числі і хімічних процесах і реакторів. Загальний аналіз точними методами, що дозволяє визначити число стаціонарних станів і їхня усталеність, є досить складною математичною задачею. Детальний розгляд цих методів виходить за рамки даного курсу, тому дамо лише їхній короткий опис. Перший метод Ляпунова заснований на аналізі коренів характеристичного рівняння і побудові траєкторій на фазовій площині. Для стійкості лінійної системи n-го порядку необхідно і досить, щоб усі n коренів її характеристичного рівняння:
розташовувалися на комплексній площині коренів p = a + bi ліворуч від мнимої осі. Як правило, математичні моделі хімічних реакторів складаються з нелінійних рівнянь. Але при малих відхиленнях від стаціонарного режиму ці рівняння можна линеаризовать в околицях стаціонарного режиму і надалі використовувати апарат дослідження лінійних рівнянь. Другий метод Ляпунова заснований на аналізі стійкості з використанням функції Ляпунова V(x), що повинна задовольняти наступним умовам:
Основна складність при використанні цього методу складається в перебуванні самої функції Ляпунова і знака її похідної. Однак при використанні цього методу для дослідження стійкості відпадає необхідність у побудові всіх траєкторій на фазовій площині. Може створитися враження, що усталеність по Ляпунову недостатня через малість збурювань, що накладаються, і необхідно розглядати "технічну" усталеність - при кінцевих збурюваннях. Дійсно, усталеність по Ляпунову, є необхідним, але, узагалі говорячи, недостатньою умовою для рішення технічних задач. Проте, у більшості практичних випадків аналіз стійкості методами Ляпунова дає і достатні умови. Якщо виникає необхідність досліджувати чутливість технологічного режиму реактора до значних відхилень від стаціонарного режиму, то використовується чисельний аналіз перехідних режимів на основі моделі, що описує нестаціонарний процес. Такий аналіз виконується на ЕОМ. Однак далеко не завжди виникає необхідність прибігати до досить складного апарата дослідження стійкості за допомогою точних методів або до досить великому дослідженню чисельними методами. У ряді випадків можна використовувати критерії стійкості. Критерії стійкості - умови, що дозволяють визначати усталеність стаціонарного стану реактора по величині його параметрів. Так, для простих схем контактних вузлів справедливий якісний підхід, заснований на обчисленні параметричної чутливості стаціонарних режимів. Усталеність простих схем Простою схемою контактного вузла називається схема, у якій мається тільки один зворотний зв'язок - вплив результатів протікання процесу на початкові умови в реакторі. Наприклад, зворотним зв'язком є зовнішній теплообмін між газовим потоком, що виходить з реактора, і вихідною реакційною сумішшю, що надходить у реактор. Зворотний зв'язок може бути також обумовлена внутрішнім теплообміном, подовжнім переносом речовини і тепла в шарі, циркуляцією реагуючих речовин і ін. При малих змінах параметрів параметрична чутливість визначається як частинна похідна функції, що характеризує технологічний режим у реакторі, по відповідному параметрі при стаціонарному режимі. Вона визначає ступінь впливу параметрів режиму і граничних умов на роботу реактора і тісно зв'язана зі стійкістю і можливостями регулювання процесом. Як приклад розглянемо просту реакторну схему, що складається з реактора з одним адіабатичним шаром каталізатора (1) і зовнішнього теплообмінника (2) з байпасом для регулювання температури перед шаром каталізатора (рис.4.1).
Для спрощення висновку приймемо, що Q2=0, тобто байпас відсутній. З теплового балансу випливає, що в стаціонарному режимі
де Q - об'ємна витрата; КT - коефіцієнт теплопередачі; F - поверхня теплообміну; Dtcp - середня різниця температур гарячого і холодного теплоносіїв; Cp, r - теплоємність і щільність реакційної суміші, відповідно.
Якщо об'ємні витрати, теплоємності і щільності обох теплоносіїв однакові, а тепловими втратами можна зневажити, то з балансу для теплообмінника
можна знайти значення Т:
Підставивши (4.5) у (4.4) одержимо:
Тоді, підставивши (4.6) у (4.3), можна записати:
чи:
Для адіабатичного шару температуру на виході можна знайти по наступному вираженню:
де DТад = (-DН) Сіх / (Cрr) - адіабатичний розігрів реакційної суміші. З (4.10) випливає, що Тк = f1(Тн). Перетворивши (4.8), одержимо:
З (4.11) видно, що початкова температура Тн залежить від результатів протікання процесу, тобто Тн = f2 (Тк). Отже, у даній схемі має місце зворотний зв'язок. Область стійкості являє собою сукупність значень параметрів, для яких дотримується умова стійкості (2.20), обумовлене в даному випадку наступним нерівністю:
З теплового балансу (4.7):
Підставивши (4.13) у (4.12), умова стійкості можна записати:
чи:
При роботі будь-якого промислового апарата дуже часто можливі різні коливання параметрів процесу. Для можливості їхньої компенсації і підтримки технологічного режиму в заданих межах передбачають байпас свіжої реакційної суміші повз теплообмінник, але при цьому трохи збільшують поверхня теплообміну. Розглянемо випадок, коли Q20. У цьому випадку умова стійкості має наступний вид:
Збільшення поверхні теплообміну приводить до збільшення параметра тепловідводу γ, що зменшує область стійкості, при якій можливий автотермічний режим. Але наявність байпасу дає можливо стабілізувати вхідну температуру. Аналіз умови (4.16) показав, що доданок, що враховує вплив байпасу Q2/(2Q1), тільки компенсує зменшення що складається QCp r/(KT Fp) у порівнянні з величиною QCpr/(KT FT), але не розширює область стійкості (тут FT. - теоретично необхідна величина поверхні теплообміну, Fp - реальна поверхня теплообміну). Отже, байпасом можна стабілізувати процес тільки в межах області стійкості, обумовленої умовою (4.12) чи (4.15), причому F=FT. Розглянемо умову (4.14). З (4.10) випливає, що Тк -Тн = DТад. Різниця Тн -Те визначає величину зміни температури вихідної суміші. Позначивши її DТнагр і підставивши в (4.14), одержимо:
Область стійкості визначається відношенням величини підвищення температури реакційної суміші в шарі каталізатора (DТад = Тк - Тн) до величини підвищення температури вихідної суміші. Співвідношення (4.17) визначає область стійкості й автотермічності процесу. Чим більше ступінь використання тепла реакційних газів, тим менше область стійкості. Умови стійкості, аналогічні (4.12), отримані і для реакторів із внутрішнім теплообміном (мал.4.2):
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 208; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.111.44 (0.009 с.) |

 Рис.4.1
Рис.4.1
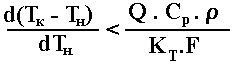

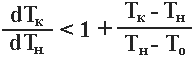
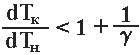


 рис.4.2
рис.4.2




