
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обчислення похідних цільової функціїСодержание книги
Поиск на нашем сайте
В основу градiєнтних засобів пошуку оптимуму покладені обчислення та аналіз похідних цільової функції R(U). Якщо аналітичний вигляд R(U) відомий, то обчислення похідних dR/dUj частіше всього не складає особливих труднощів. Інакше єдиним засобом визначення похідних є чисельні засоби. Значення похідної може бути обчислено за формулою:
де ΔUj – величина приросту незалежної перемінної Uj. Формула (5.39) дає лише наближене значення похідної. Точність наближення залежить від величини припущення ΔUj. Методів провіщання найкращого значення ΔUj не існує. Практично для визначення прийнятної величини припущення(особливо на початку пошуку, коли похідні ще не знаходились) використовується метод дробіння ΔUj. Наприклад, розраховується значення похідної з припущенням, рівним ΔUj. Після цього розрахунок повторюється з ΔUj/2. Якщо отримані значення похідних розрізняються істотно, то розрахунок повторюється з ΔUj/4 і т.д., поки не буде знайдено прийнятне значення припущення. На наступних кроках пошуку це значення припущення може уточнюватися.
Засіб релаксації.
Алгоритм засобу являє собою пошук осьового напрямку, вдовж якого цільова функція зменшується найбільш сильно. Для цього в початковій точці пошуку визначають похідні оптимiзуємої функції по всім незалежним перемінним. Осьовому напрямку з найскорішим спаданням цільової функції, очевидно, відповідає найвелика за модулем похідна. Якщо знак похідної від'ємний, то цільова функція зменшується у напрямку осі, якщо позитивний - то у протилежному напрямку. За напрямком спадання цільової функції виконуються кроки до тих пір, поки не буде отримане мінімальне значення за обраним осьовим напрямком. Тоді знов визначають похідні по всім напрямкам, за винятком того, по якому здійснюється спуск. Знову знаходять осьовий напрямок найскорішого спадання цільової функції, по якому виконуються подальші кроки і т.д. Критерієм закінчення пошуку оптимуму є досягнення такої точки, при руху з якої по будь-якому осьовому напрямку подальшого спадання функції не походить. На практиці, для признаку оптимуму часто застосовують умову:
Умова (5.40) може бути використана у отому випадку, коли оптимум лежить всередині допустимої області зміни незалежних перемінних. Якщо ж оптимум припадає на межу області допустимої зміни перемінних V, тоді критерій (5.40) не придатний та замість нього треба застосовувати умову позитивності всіх похідних за допустимими осьовими напрямками. При цьому допустимим осевим буде напрямок всередині області V. Алгоритм спуску для обраного осьового напрямку може бути записаний у вигляді:
Причому:
sign - функція знаку ("сiгнум"); Up - вектор точки, у якій останній раз виконувалось обчислення похідних цільової функції.
Графічне зображення руху від вихідного стану до оптимального показано на рис. 5.16. При занадто малій величині кроку число кроків, що необхідно зробити, щоб досягнути оптимума, буде великим та, отже, буде потрібний великий обсяг розрахунків. Якщо ж величина кроку обрана великою, то поблизу оптимуму може відбуватися "нишпорення", тому що при великій величині кроку мала імовірність попадання в околицю оптимуму, в якій виконується умова (5.40). Рис.5.16
Найпростіший алгоритм використання перемінного кроку пошуку складається в наступному. На початку спуска по одному з осьових напрямків задається деякий крок h. З цим кроком виконується спуск по обраному осьовому напрямку до отих пір, поки для двох наступних обчислювань значення цільової функції виконується умова (при пошуку мінімуму)
При порушенні умови на будь-якому кроці напрямок спуска по осі змінюється на протилежний, та спуск продовжується з останньої разрахованої точки зі зменшеною вдвічі величиною кроку. Цей алгоритм може бути записаний наступним чином:
Внаслідок використання такої стратегії крок спуска по осьовому напрямку буде зменшуватися в районі мінімуму цільової функції по цьому напрямку та пошук мінімуму можна припинити, коли величина кроку hk стане менше заданої точності визначення мінімуму e у осьовому напрямку. Після цього знаходиться новий осьовий напрямок, в якому функція змінюється найбільш сильно. Початковий крок по новому напрямку вже можна обрати з урахуванням величини кроку по попередньому напрямку. Це дозволяє автоматично зменшувати початковий крок по мірі наближення до оптимуму, у районі якого спуск по кожній осі проходить на невелику віддаль.
Рис.5.17 Рис.5.18
У першому випадку для досягнення мінімуму цільової функції необхідно тільки два циклу руху уздовж осьових напрямків, в другому число таких циклів зростає надто істотно. При використанні метода релаксації інколи виникають чималі труднощі: а) при наявності обмежень пошук оптимуму може "застрягати" в будь-якій точці межі (рис. 5.19). б) при наявності "байраків", напрями яких не співпадають з осями (рис. 5.20).
Рис.5.19 Рис.5.20
Метод градієнту
У даному засобі використовується градієнт цільової функції. На відміну від засобу релаксації в даному засобі кроки учиняються на напрямку найбистрішого зменшення цільової функції, а не по осьовим напрямкам. Такий підхід, природно, прискорює процес пошуку оптимуму. Процес пошуку оптимуму у засобі градієнту також здійснюється в два етапу. На першому знаходяться значення приватних похідних по всім незалежним перемінним, що і визначає напрямок градієнту в точці,що розглядається. На другому етапі здійснюється крок в напрямку, зворотному напрямку градієнту, тобто у напрямку найскорішого спадання цільової функції. При виконанні кроку одночасно змінюються значення всіх незалежних перемінних. Кожна з них отримує припущення, пропорційне відповідної що складає градієнт по наданій осі. По суті в засобі градієнту застосовує ота ж інформація про цільову функцію, що і в засобі релаксації при виборі осьового напрямку, але спуск виробляється по оптимальному шляху. Алгоритм градiєнтного пошуку може бути записаний наступним образом:
(5.43)
В алгоритмі (5. 43) для градiєнтного пошуку застосовується нормалізований вектор градієнту, зазначаючий лише напрямок найскорішого зміну цільової функції, але він не зазначає швидкості зміни по цьому напрямку. При цьому крок пошуку визначається величиною hк, стратегію зміни якої можна будувати незалежно від абсолютної величини градієнту. Можна використовувати інший алгоритм градiєнтного засобу у виді: Uk+1j=Ukj - h0 dR(Uk)/dUj (5.44)
В цьому випадку величина кроку ΔUKj= -h0 dR(UK)/dUj при постійному значенні параметра h змінюється автоматично відповідно до зміною абсолютної величини градієнту. Алгоритм (5.44) володіє отим достоїнством, що при наближенні до оптимуму величина кроку ΔUкj автоматично зменшується. Взагалі, задача вибору стратегії зміни величини кроку у градієнтнім пошуку більш важна, чим в засобі релаксації, тому що після кожного кроку тут необхідно знаходити похідні цільової функції, розрахунок яких пов'язаний з обчисленням n значень цільової функції. Дрібний крок вимагає великого обсягу вичислений, при великому кроці - можливо " рисканiє " в районі оптимуму. Момент закінчення пошуку визначається по заздалегідь заданим умовам. Один з можливих варіантів - виконання нерівняння (5. 40). Інший варіант після кожної серії з заданим числом кроків S запам’ятається значення цільової функції. Число кроків S у серії вибирається таким, щоб на початкових етапах пошуку діялося помітна зміна значення цільової функції (R). Якщо наступна серія кроків дає менше значення R, отже пошук продовжується. Якщо ж при виконанні слідкуючої серії менше значення R не знаходиться, отже пошук припиняється таі одержане найменше значення роздивляється як iскомий оптимум. Браком градiєнтного засобу є отже, що при його використанні можна виявити тільки локальний мінімум. Для отого, щоб знайти у функції інші локальні мінімуми, необхідно проводити пошук з інших початкових точок. Таким чином, за допомогою засобу градієнту кожний локальний мінімум цільової функції можна охарактеризувати деякою областю "притяжіння", що володіє отієї властивістю, що при завданні початкового стану U в кордонах цієї області засіб градієнту завжди приводить в один і отой же локальний мінімум. Розглянемо один з простіших алгоритмів реалізації засобу градієнту. Вибираємо координати початкової точки U1n U2n, величину кроку H1 та H2, припущення e1 та e2.
(5.45)
Для розрахунку ΔR необхідно обчислити величини похідних dR/dUi.
(5. 46)
(5. 47)
Рис 5.21
Після цього роблять крок в точку 2 для наступного розрахунку R(Х1 Х2). Координати цієї точки визначаються по формулі:
(5.48)
Подальший алгоритм розрахунків будують по-різному. В простому варіанті можна просто повторювати описану вище процедуру. Якщо ж крок невдалий - в цьому випадку крок зменшують вдвічі та розраховують точку i+2. Тепер, якщо зменшений крок був удалий, отже рухатися по отому ж напрямку немає змісту, тому що прийдемо в "погану " точку i+1. В цьому випадку біля точки i+2 ставляться допоміжні точки, розраховуються похідні та визначається нове направлення градієнту. Якщо ж і зменшений крок не приведе в "гарну" точку, отже повертаємося в точку i та будемо шукати новий напрямок градієнту в неї
Засіб найскорішого спуска
При використанні засобу градієнту на кожному кроці треба визначати значення всіх приватних похідних функції, що оптимізується, по всім незалежним перемінним, що вимагає великого обсягу обчислювань. Засіб релаксації володіє в цьому змісті визначеними перевагами, тому що при спускові вдовж обраного осьового напрямку не вимагає обчислення похідних. Але рух походить не у оптимальному напрямку. Поєднання основних ідей засобу релаксації та градієнту дає засіб найскорішого спуска, суть якого укладається у слідкуючому. Після того, як в початковій точці знайдений градієнт функції, що оптимізується, та отим самим визначено напрямок її найскорішого спадання, отже в разі пошуку мінімуму цільової функції в наданому напрямку робиться крок спуска. Якщо значення цільової функції в результаті кроку зменшилося, отже виробляється черговий крок в цьому напрямі, та так до отих пор, поки у цьому напрямку не буде знайдений мінімум цільової функції. Після цього обчислюється градієнт та визначається новий напрямок найскорішого спадання цільової функції.
Очевидно, що менш різко змінюється напрямок градієнту цільової функції, отим краще використати засіб найскорішого спуска у порівнянні з засобом градієнту тобто вдалині від точки оптимуму. Поблизу оптимуму напрямок градієнт змінюється різко, тому засіб найскорішого спуска автоматично переходить у засіб градієнту, тому що мінімум по кожному напрямку знаходиться за невелика кількість кроків (рис.5.22).
Рис. 5.22
Важливою особливістю засобу найскорішого спуска є отже, що при його застосуванні кожний новий напрямок ортогонален попередньому. Це пояснюється отим, що рух в одному напрямку виробляється до тих пор, поки напрямок руху не опиниться дотичною до якої-або лінії постійного рівня так же як і у засобі релаксацiї. Але на відміну від засобу релаксації бистрота сходимості до точки оптимуму не залежить від орієнтації системи координат. У вигляді критерію закінчення пошуку можуть використовуватися оті ж умови, що і у засобах релаксації та градієнту. Крім отого, можна використовувати наступне співвідношення:
(5.49)
де UА j, UB j - координати початкової та кінцевої точок останнього відтинку спуска. Цей же критерій може використовуватися у поєднанні з контролем значень цільової функції у точках UA та UB:
| R(U(F))-R(U(B)) | (5.50)
|
||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 457; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.156.91 (0.007 с.) |

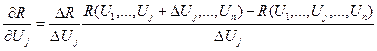 (5.39)
(5.39)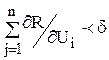 (5.40)
(5.40)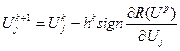 (5.41)
(5.41)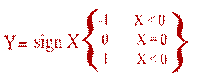
 - значення змінюємої перемінної на к-ом кроку спуска;
- значення змінюємої перемінної на к-ом кроку спуска;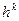 - величина к-го кроку, що може змінювати своє значення залежно від номеру крока;
- величина к-го кроку, що може змінювати своє значення залежно від номеру крока;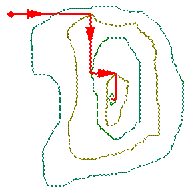 Очевидно, що швидкість руху до мінімуму залежить від отого, наскільки вдало обрано крок
Очевидно, що швидкість руху до мінімуму залежить від отого, наскільки вдало обрано крок 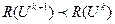
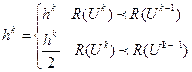 (5.42)
(5.42)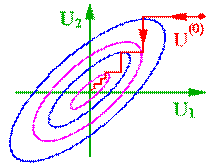 Істотною особливістю метода релаксації є залежність часу пошуку від орієнтації системи координат (рис. 5.17 та 5.18).
Істотною особливістю метода релаксації є залежність часу пошуку від орієнтації системи координат (рис. 5.17 та 5.18).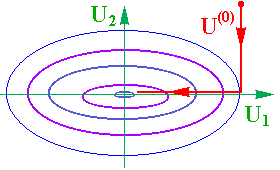


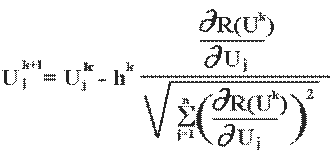
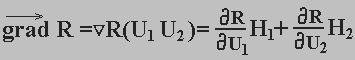 Визначимо градієнт цільової функції
Визначимо градієнт цільової функції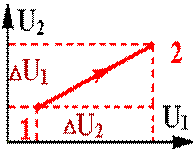 Визначимо їх численними засобами. Біля початкової крапки 1 з координатами (U1n,U2n) ставляться дві допоміжні крапки: 1’- на відстані ε1 уздовж осі U 1 і 1''- на відстані ε2 уздовж осі U2 (рис. 5.21)
Визначимо їх численними засобами. Біля початкової крапки 1 з координатами (U1n,U2n) ставляться дві допоміжні крапки: 1’- на відстані ε1 уздовж осі U 1 і 1''- на відстані ε2 уздовж осі U2 (рис. 5.21) 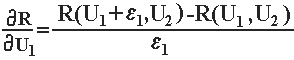
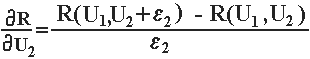
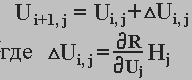
 Однак, частіше роблять інакше. Якщо крок опинився вдалим, отже роблять ще крок в тому ж напрямку, використовуючи знайдені значення похідних на попереднім кроці. Практично це вже не буде напрямком градієнту, але якщо наступний крок дає потрібне припущення R (Х1 Х2), отже це дозволить "зекономити" на розрахунку похідних. Якщо і цей крок удалий, отже можна зробити крок ще раз і так далі.
Однак, частіше роблять інакше. Якщо крок опинився вдалим, отже роблять ще крок в тому ж напрямку, використовуючи знайдені значення похідних на попереднім кроці. Практично це вже не буде напрямком градієнту, але якщо наступний крок дає потрібне припущення R (Х1 Х2), отже це дозволить "зекономити" на розрахунку похідних. Якщо і цей крок удалий, отже можна зробити крок ще раз і так далі.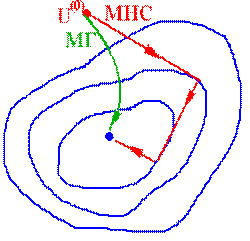 В зіставленні з засобом градієнту засіб найскорішого спуска виявляється більш вигідним із-за скорочування обсягу обчислювань. По суті, засіб наiскорішого спуска по обчислювальним витратам еквiвалєнтєн засобу релаксації, але вигідно відрізняється від нього отим, що принаймні перші кроки після визначення градієнту виробляються у оптимальному напрямку.
В зіставленні з засобом градієнту засіб найскорішого спуска виявляється більш вигідним із-за скорочування обсягу обчислювань. По суті, засіб наiскорішого спуска по обчислювальним витратам еквiвалєнтєн засобу релаксації, але вигідно відрізняється від нього отим, що принаймні перші кроки після визначення градієнту виробляються у оптимальному напрямку.



