
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифузійна модель з подовжнім переносом речовини та теплаСодержание книги
Поиск на нашем сайте
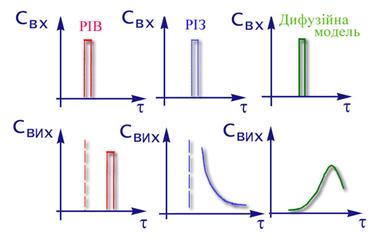
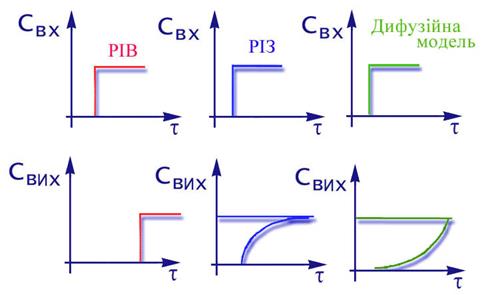
Далеко не завжди вдається описати процес,який протікає у промисловому реакторі, ідеальними моделями.Так,наприклад, для порівняно невеликих по довжині реакторів при малих лiнейних швидкістях потоку реакційної суміші для опису адiабатичного режиму протікання процесу не підходить ані РІЗ, ані РІВ. Очевидно, що ми маємо справу з деякою проміжною нагодою, де має місце неповне змішення по потоку, т.є. на режим ідеального витиснення накладається часткове перемішення. Це підтверджується iмпульснимi та разгонними характеристика ми дифузійної моделі,що показують реакцію об'єкту при нанесенні на вході iмпульсного або стрибкообразного обурення (рiс.2.19, 2.20)
Рис 2.19. Iмпульсні характеристики (τ- час перебування суміші у реакторі).
Рис 2.20. Разгонні характеристики
Характер процесів переносу визначається двома складовими: 1.конвективной – яка відповідна режиму ідеального витиснення; 2.дифузійної – яка описує гуртовий вплив різноманітних факторів,що виражаються у відході одніх часток потоку вперед і відставанні інших
Рис.2.21 Для опису другої складової використовуємо закон Фіка:
де qм - кількість речовини, що дифундує у прямому та зворотному напрямку; DL - ефективний коефіціент продольной дiффузii; dc/dz- градієнт концентрації; S - площа поперечного перетину. Знак " - " у порівнянні (2.48) показує,що дифузійний потік завжди скерований вбік зменшення концентрації. Складемо математичну модель дифузійної моделі. Матеріальний баланс:
У порівняннi (2.49) перші два доданка враховують перенос речовини через нижній кордон виділеного елементарного обсягу: перше - прихід за рахунок конвективного потоку, друге - унос за рахунок дифузійного потоку.Третій та четвертий доданок - перенос речовини через верхній кордон:третє - унос з конвективним потоком, четверте - прихід за рахунок дифузійного потоку. П'ятий доданок враховує зміну кількості речовини за рахунок хімічної реакції. В правої частині - зміна кількості речовини у виділеному елементарному обсязі в часу. Після скорочення і ділення на SdZ одержимо:
Порівняння (2.50) становить матеріальний баланс однопараметричної дифузійної моделі.Перший доданок враховує перенос речовини за рахунок конвективного потоку,другий - за рахунок дифузійного потоку, третій-за рахунок хімічної реакції. Pівняння енергогетичного балансу складається аналогічно, а замість закона Фіка використовується закон Фур'є:
де qТ - кількість теплоти,яка переноситься за рахунок теплопроводтностi; aL - ефективний коефіціент продольної теплопроводностi; dT/dz- градієнт температур. Знак " - " у (2.51) означає,що передача тепла здійснюється у сторону зменшення температури.
Перетворив (2.52),одержимо порівняння енергетичного балансу:
Порівняння кiнетики й початкові умови аналогічні моделі РIВ: W = f(Т,С) (2.54) Т = ТПОЧ (Z) С = CПОЧ (Z) (2.55) Краєві (кордонні) умови необхідно задавати як на вході, так і на виході із реактора. Для висновку цих умов у загальному віпадку необхідно скласти матеріальний та тепловий баланси для вхідного та вихідного перетина реактора. На відміну від балансів, які виводяться для елементарного обсягу, в даному випадку не враховуються зміни за рахунок хімічної реакції та накопичування, тому що товщина шару dZ=0 та отже, доданкі, що містять dZ, також дорівнюють 0. Спочатку розглянемо перетин Z=0:
Після перетворень одержимо кордонні умови у наступному виді: Z = 0: При Z=L, т.є. на виході з реактора, як правило,швидкість хімічного перетворення вкрай мала,оскільки процес виходить або на повну, або на рівноважну міру перетворення.Отже, градієнти температур та концентрацій відсутні. Тому можна записати: Z = L: dС/dZ=0; dТ/dZ=0; (2.59)
|
|||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 228; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.150.195 (0.01 с.) |

 Спершу розглянемо одномірний випадок – перенос речовини здійснюється тільки у продольному напрямку. Така модель отримала назву однопараметрична дифузійна модель (рiс.2.21). Висновок рівнянь балансів здійснюється аналогічно РІВ.
Спершу розглянемо одномірний випадок – перенос речовини здійснюється тільки у продольному напрямку. Така модель отримала назву однопараметрична дифузійна модель (рiс.2.21). Висновок рівнянь балансів здійснюється аналогічно РІВ.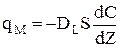 (2.48)
(2.48)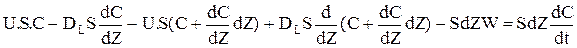 (2.49)
(2.49)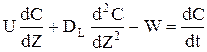 (2.50)
(2.50)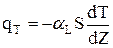 (2.51)
(2.51)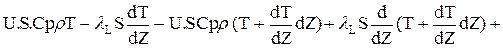
 (2.52)
(2.52)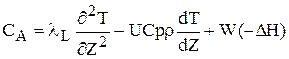 (2.53)
(2.53)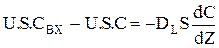 (2.56)
(2.56)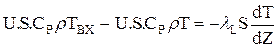 (2.57)
(2.57)
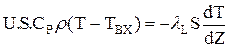 (2.58)
(2.58)


