
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зіставлення засобів побудови математичних моделейСодержание книги
Поиск на нашем сайте
Вибір засобу залежить від важливості та міри важкості процесу. Для дорідних багаготонажних виробництв необхідні хороші моделі, тут застосовують теоретичний засіб. Цим же засобом користуються при утворенні принципово нових технологічних процесів. Для дрібних виробництв зі складним характером процесу використовують експериментальний засіб. На практиці, як правило, використовується разумне поєднання всіх засобів. Вірогідність та простота моделі Збудована однім з розглянених вище засобів математична модель одночасно повинна задовольняти вимогам вірогідності та простоти. Достовірна модель, яка правильно описує поводження об'єкту, може опинитися надто складної. Складність моделі визначається, як правило, складністю об'єкту, що досліджується та мірою точності, що пред'являє практикою до результатів розрахунку. Необхідно, щоб ця складність не переважала деякої межі, що визначається можливостями існуючого математичного апарату. Отже, модель повинна бути достатньо простою у математичному відношенні, щоб її можна було вирішити наявними засобами та коштами. Рішення порівнянь математичного опису При рішенні порівнянь математичного опису з використанням ЕОМ необхідно утворення моделюючого алгоритму ("машинної" моделі). Моделюючий алгоритм є перетвореним математичним описом та становить послідовність арифметичних та логічних операцій рішення, записану у вигляді програми. При розробці такого алгоритму раніше всього необхідно обрати засіб рішення порівнянь математичного опису – аналітичний чи численний. Треба пам'ятати про необхідність перевірки точності обраного засобу розрахунку. Інколи із-за обмеженості існуючих засобів приходиться спрощувати математичний опис. В цьому випадку необхідна оцінка внесеної при цьому похибки Перевірка адекватності та iдентифікація моделі Перевірка адекватності - це оцінка вірогідності збудованої математичної моделі, дослідження її відповідності об'єкту, що вивчається. Перевірка адекватності здійснюється на тестових експериментах шляхом порівняння результатів розрахунку по моделі з результатами експерименту на об'єкті, що вивчає при однакових умовах. Це дозволяє установити кордони застосовності побудованої моделі.
Основним етапом в побудові адекватної моделі є iдентифікація математичного опису об'єкту. Задачею iдентифікації є визначення виду моделі та знаходження невідомих її параметрів - окремих констант або їх комплексів, що характеризують властивості об'єкту. Iдентифікація можлива при наявності необхідної експериментальної інформації про об'єкт, що вивчає. Вибір математичної моделі Задача вибору моделі виникає при наявності для одного й отого ж об'єкту класу моделей. Вибір моделі є одним з найважливіших етапів моделювання. В кінцевому рахунку перевага отієї чи іншої моделі визначає критерій практики, що розуміє у широкому змісті. При виборі моделі треба сходити з розумного компромiсу між важкістю моделі, повнотою характеристик,що одержують з її допомогою об'єкту та точністю цих характеристик. Так, якщо модель недостатньо точна, оте її треба доповнити, уточнити введенням нових факторів може також опинитися, що надана модель занадто важка та оті ж результати можна отримати за допомогою більш простої моделі.
Моделювання Хімічних Реакторів На основі математичних моделій хімічних реакторів вирішуються наступні завдання: - вибір конструкції та розмірів реакторів; - визначення оптимальних режимів роботи; - дослідження і оптимiзація процесів та реакторів; - розробка систем автоматичного управління. Нижче будуть розглянуті ряди математичних моделій реакторів, що найбільш часто використовуються на практиці. Модель реактора ідеального змішування Особливістю моделі реактора ідеального змішування (РІЗ) є те, що концентрація і температура однакові по всьому об`єму реактора та дорівнює відповідним значенням на виході. Схематично модель РІЗ приведена на рис. 2.1
Тх - температура хладогента Qi -об'ємна витрата; Сi - концентрація ключевого компоненту; Ti - температура; Індекси: вх. - вхід, вих.- вихід
Рис.2.1
Оскільки в РІЗ змішування діється миттєво по всьому реактору, то Свих=C, Твих = Т. Для спрощення також приймемо, що Qвх = Qвих = Q. Позначимо: V - обсяг реактору; S - поверхня теплообміну; W - швидкість хімічного перетворення. Матеріальний баланс записується на основі закону збереження кількості речовини:
Перетврюємо: Дорівнення (2.2) стає дорівненням матеріального балансу РІЗ. Енергетичний баланс записується на основі закону збереження енергії:
де C Р - теплоємність реакційної суміші; p - густота реакційної суміші; a - коефіціент теплопередачi; S - поверховість теплообміну; Cа - усереднена об'ємна теплоемність апарату. CA = CR×xR×rR + CP×xP×rP + CK×xK×rK де xR, xP, xK - частка загального обсягу,що займається внутрішніми конструкціями,реакційною середою й каталізатором,відповідно; CR, CP,Ck - теплоємністі конструкціі реактору, реакційноі середи та каталізатора, відповідно; ×rR, rP, rK - густота матеріалу реактора,реакційноі середи, та каталізатору, відповідно. Перетворюємo дорівняння (2.3)
Дорівнення (2.4) стає дорівненнєм теплового балансу РІЗ. Дорівнення кінетикі. В загальному виді швидкість реакціі визначається як функція составу та температури реакційноі суміші: w =F(C,T) (2. 5) де: C - вектор концентрацій, T - температура;
а) проста реакція: W= kf(C); де: k - константа швидкісті реакціі,що визначається по дорівненню Аррейніуса: k = k0 * e –E/RT де: k0- предекспонента; E -eнергія актіваціі;
в) оборотна реакція: _ _ W=k1 f1 (C)-k2 f2 (C) де: k1- константа швидкісті прямої реакції, k2 - константа швидкісті зворотної реакції. Початкові умови. Початкові умови визначають поля температур та концентрацій в початковий момент часу, що, взагалі кажучи,може бути обрано довільно. t = 0; C = C поч ; T = Tпоч ; (2. 6) Обмеження. Визначають діапазон параметрів,в яких працює реактор.
Tmin < T < Tmax (Tmin і Tmax - робочий діапозон температур) Cвх min < Cвх < Cвх max (Cвх min і Cвх max - робочий діапозон вхідних концентрацій) Qmin< T < Qmax (Qmіn і Qmax- робочий діапозон oб'ємноі витрати)
|
||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 233; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.44.8 (0.01 с.) |

 Приймемо наступні обозначення:
Приймемо наступні обозначення: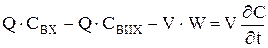 (2. 1)
(2. 1) (2. 2)
(2. 2) (2.3)
(2.3) (2.4)
(2.4)


