
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Встановлення рівнянь руху в моделюванні економікиСодержание книги
Поиск на нашем сайте Один з напрямів моделювання економіки ґрунтується на застосуванні теоретичних досягнень природознавчих наук, зокрема – теоретичної механіки, електротехніки. В цих науках вироблено два альтернативні підходи до теоретичного вивчення реальних явищ. Це метод встановлення так званих рівнянь руху і метод визначення функції Лагранжа. В теоретичній механіці рівняннями руху називають систему звичайних диференціальних рівнянь, які описують зміну з часом координати взаємодіючих тіл. Просторовий рух механічного тіла зручно описувати у так званій канонічній системі координат, з допомогою рівнянь Гамільтона
де Рівняння Гімільтона задають «повний опис стану» механічної системи, виражений значеннями канонічних координат (які також є канонічними змінними стану системи Опис механічних об'єктів з допомогою рівнянь руху називають «класичним наближенням», оскільки ці рівняння ґрунтується на двох «класичних теоріях» ‑ теорії диференціальних рівнянь і теоретичній механіці. Така «класична теорія» була також розроблена для електротехнічних об'єктів і завдяки цьому досягнення теорії диференціальних рівнянь стали основою інженерної освіти. Поширення цих досягнень на економічні науки привело до становлення «економічної кібернетики» як міждисциплінарної науки, яка базується передусім на досягненнях названої вище «класичної теорії диференціального числення». Запозичуючи названий вище досвід «повного і вичерпного опису» об'єкту у формі системи звичайних диференціальних рівнянь першого порядку відносно «змінних стану» («важливих параметрів», що описують внутрішню природу об'єкта) моделі економічних об'єктів також зручно записувати у формі подібній до «рівнянь руху» класичної механіки. За фізичною аналогією в математичних моделях економічних об'єктів рівняннями руху називають систему звичайних диференціальних рівнянь першого порядку в канонічній формі. Тобто у формі, розв'язаній відносно перших похідних невідомих функцій. Невідомими функціями часу в таких рівняннях руху економічного об'єкта є практично важливі економічні величини. Наприклад – величина капіталу, ресурсів, доходу. У класичній механіці канонічні змінні мають строго визначені, принципові властивості. В моделях економіки вибір аналогічних «змінних в рівняннях руху» не мають такого строгого обґрунтування. Їх вибирають на основі практичних потреб та обчислювальних можливостей. Додамо, що рівняння руху, записані у канонічній формі, є зручними для розв'язування їх з допомогою числових методів. Власне числові методи розв'язування систем звичайних диференціальних рівнянь було розроблено передусім для таких рівнянь. Інший підхід до теоретичного опису механічних тіл у класичній теорії ґрунтується на встановленні функції Лагранжа
дають рівняння руху, які називають рівняннями Якобі. Аналогом функції Лагранжа в моделюванні економіки є критерії, що відображають екстремальні принцип економічної поведінки. Серед таких принципів ринкової економіки – стратегії досягнути найбільшого доходу, найшвидшого доходу, найкращої адаптації до ринку, найкращого слідування якомусь типу поведінки. Наприклад – поведінки конкурента, чи дотримання середньо-ринкової тенденції. Додамо, що такі екстремальні принципи економічної поведінки є частковим виявом екстремальної поведінки живої речовини, встановлених В.І.Вернадським. Наприклад – прагненням живих організмів жити якомога довше, привести в рух якомога більше речовини, зайняти якомога більший ареал існування. Економічні аналоги функції Лагранжа ‑ це критерії, які задають умову оптимального управління в технічних й економічних задачах.
Практика моделювання показує, що розробити математичну модель економічного об'єкта у формі «функції, яка задає критерій економічної поведінки» (аналог функції Лагранжа), опираючись лише на апріорну інформацію є принаймні «дуже незручно». Тим часом – рівняння руху для економічних об'єктів встановити нескладно на основі емпіричних спостережень. Тому в задачах моделювання економіки, особливо при дослідженні нових, мало вивчених процесів зручніше опиратися на метод встановлення рівнянь руху. Для встановлення рівнянь руху економічного об'єкта необхідно повторити низку пізнавальних дій, прийнятих у емпіричних дослідженнях. Назвемо їх. Спершу необхідно вибрати в модельованому об'єкті величини, які мають кількісний вимір (в фізичних чи грошових одиницях), і які є суттєвими для досліджуваного об'єкта. Це умовний аналог «узагальнених координат» класичної механіки. В економіці такі величини ще називають параметрами, показниками, характеристиками. Далі, зіставляючи емпіричні спостереження за досліджуваним об'єктам з його економічною суттю – встановити вербальне правило поведінки. Це словесно виражене правило поведінки описує закономірність емпірично спостережуваної поведінки об'єкта. З погляду методології пізнання правило поведінки є простим емпіричним узагальненням. Додамо, що «правила поведінки» необхідно встановлювати на основі емпіричних спостережень, а за ідеологічними переконаннями. Порушення цієї умови веде до гносеологічних помилок, які мають надзвичайні соціально-економічні наслідки. Цінність такого правила поведінки для розроблення моделі в тому, що воно відображає емпірично спостережуваний зв'язок між величинами, котрі описують об'єкт, і слугує основою для запису математичного рівняння (встановлення рівняння руху). Правило поведінки є не чим іншим як емпірично встановленим і вербально вираженим рівнянням руху. Для розроблення математичної моделі економічного об'єкта необхідно встановити правила поведінки для всіх змінних стану проектованої моделі і записати для кожної з них відповідне диференціальне рівняння першого порядку. Проілюструємо встановлення рівняння руху на прикладі депозитного вкладу. Емпірично відомо, що залишок на депозитному вкладі зростає тим швидше, чим більший залишок і, чим вища ставка за кредит. Цей емпіричний факт описує таке правило поведінки. «Швидкість зміни депозитного вкладу прямо пропорційна розміру вкладу». З цього правила поведінки очевидно випливає рівняння руху: Для дослідження ринкової економіки, особливо – вивчення її найзагальніших закономірностей доцільно застосувати власне «класичне наближення». Тому нижче більшість моделей будуть описані в рамках класичної, або її ще називають Ньютонівської теорії (за іменем розробника основ механіки й теорії диференціального й інтегрального числення). Тобто – будемо розглядати моделі економічних об'єктів у формі канонічних систем звичайних диференціальних рівнянь (що є економічними аналогами «рівнянь руху» з класичної механіки), встановлених на основі емпіричних спостережень за ринковою економікою. Зупинимося на двох зауваженнях щодо дослідження ринкової товарної економіки. Особливість економіки товарного виробництва в тому, що її учасники виробляють продукт, котрий відповідає їхньому таланту освіті, здібностям (чи є наслідком випадкового збігу обставин) і продають його за гроші, щоб за них купити у інших таких же виробників, котрий вони також виробляють для збуту за гроші. Товарне виробництво відрізняють від натурального виробництва, від економіки збирання плодів. В ринкових умовах регулювання економічних відносин відбувається передусім через розв'язання протиріч між учасниками економіки при малому (обмеженому) втручанні в це регулювання держави, інших суспільних інститутів. В політичній економіці, в гуманітарних напрямах економічної науки, в політичній пропаганді нерідко ринкову економку ідеалізують, приписують їй властивості абсолютної досконалості. Тим часом, відомо, що ринкова економіка, які й інші напрями діяльності людини, має як позитивні, корисні, плідні властивості, так і шкідливі, руйнівні. Ці дві сторони ринкової економіки є наслідком вільного вибору людини. Задача об'єктивного наукового пізнання полягає не лише у дослідженні закономірностей розвитку ринкової економіки товарного виробництва, а й в тому, щоб дати їм оцінку, схвальну або критичну, з погляду гуманітарних духовних цінностей. В цьому полягає бінарність аксіальних оцінок вивчення господарських відносин людини. Іншими словами, приступаючи до вивчення ринкової економіки, необхідно відмежовуючись від пропагандистського тиску, розрізняти плідні й деструктивні наслідки тих чи інших ринкових процесів. Питання до параграфу В чому особливість методів моделювання, які ґрунтуються на досягненнях природознавчих наук? Що називають рівняннями руху в класичній динаміці? Яку систему координат називають канонічною в теоретичній механіці і як досвід моделювання механічного руху запозичують при моделюванні економіки? Що називають рівняннями Гамільтона і які можливі їх аналогії при моделюванні економіки? В чому суть «класичного наближення» при моделюванні реальних об'єктів? Як співвідноситься предмет пізнання «економічної кібернетики» і класичне наближення в моделюванні економіки? Яке значення мають розвязки рівнянь руху при моделюванні економіки? Яке значення числових методів при розвязуванні задач моделювання? Що називають функцією Лагранжа і яке значення має досвід розроблення функцій Лагранжа в моделюванні економіки? Що таке рівняння Якобі, і як досвід розроблення цих рівнянь застосовують в моделюванні економіки? Як повязані рівняння Якобі і принципи екстремальної поведінки, встановлені В.Вернадським? В чому схожість і розбіжність між підходами «методу рівнянь руху» і «методу функції Лагранжа». Що є умовним аналогом «узагальнених координат» в моделюванні економіки? Що таке «правила поведінки» і яке їх значення в модельній інженерії? Що таке «просте емпіричне узагальнення» і яке його значення в моделюванні поведінки людини? В чому гносеологічна помилка, якщо модель розробляють не за емпіричними даними, а на основі ідеологічних переконань? Які соціальні наслідки розроблення моделей за ідеологічними твердженнями, а не за емпіричними даними? Яка цінність правил поведінки при розробленні математичної моделі? Що таке змінні стану (динамічні змінні) динамічної моделі? Чим відрізняються параметри і динамічні змінні моделі? В чому полягає актуальність застосування класичної динаміки при моделюванні економіки?
|
||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 252; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.133.172 (0.011 с.) |

 ,
,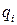 ‑ так звані узагальнені координати;
‑ так звані узагальнені координати;  ‑ узагальнені імпульси
‑ узагальнені імпульси  того тіла; (разом
того тіла; (разом  називають канонічними координатами);
називають канонічними координатами); 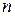 ‑ кількість тіл;
‑ кількість тіл;  ‑ функція Гамільтона, яка має сенс енергії взаємодіючих тіл. Простота і зручність цих канонічних рівнянь руху Гамільтона підштовхує дослідників з інших теоретичних наук розробити для досліджуваних ними об'єктів (в тому числі ‑ економічних) подібні рівняння, які б відзначалися такою ж математичною простотою запису та універсальністю застосування.
‑ функція Гамільтона, яка має сенс енергії взаємодіючих тіл. Простота і зручність цих канонічних рівнянь руху Гамільтона підштовхує дослідників з інших теоретичних наук розробити для досліджуваних ними об'єктів (в тому числі ‑ економічних) подібні рівняння, які б відзначалися такою ж математичною простотою запису та універсальністю застосування. диференціальних рівнянь) ‑ починаючи від поточного їх стану
диференціальних рівнянь) ‑ починаючи від поточного їх стану  в момент часу
в момент часу 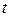 до нескінченності в прямому і зворотному напрямах зміни часу
до нескінченності в прямому і зворотному напрямах зміни часу  . Для реальних тіл така точність моделювання є умовною, адже самі тіла мають менший час існування. Проте, на обмежених проміжках часу рівняння Гамільтона мають не лише прийнятну точність, ‑ вони відтворюють суть механічного руху.
. Для реальних тіл така точність моделювання є умовною, адже самі тіла мають менший час існування. Проте, на обмежених проміжках часу рівняння Гамільтона мають не лише прийнятну точність, ‑ вони відтворюють суть механічного руху. , котра також «повно і точно» описує стан механічних тіл. Екстремуми функції Лагранжа
, котра також «повно і точно» описує стан механічних тіл. Екстремуми функції Лагранжа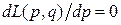 ,
, 

 , де
, де 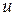 ‑ розмір вкладу (з капіталізацією відсотків),
‑ розмір вкладу (з капіталізацією відсотків),  ‑ (процентна) ставка за депозит. В цій моделі, заданій одним рівнянням, відразу бачимо особливості «класичного наближення» при моделюванні економіки. Припускається, що «відсотки» за депозит банк начисляє вкладнику неперервно, кожної миті. В дійсності ж банк додає відсотки до вкладу періодично у дні, вказані окремим договором. Тим не менше, при великих значеннях таких модельованих величин рівняння руху адекватно відображають досліджуваний економічний процес.
‑ (процентна) ставка за депозит. В цій моделі, заданій одним рівнянням, відразу бачимо особливості «класичного наближення» при моделюванні економіки. Припускається, що «відсотки» за депозит банк начисляє вкладнику неперервно, кожної миті. В дійсності ж банк додає відсотки до вкладу періодично у дні, вказані окремим договором. Тим не менше, при великих значеннях таких модельованих величин рівняння руху адекватно відображають досліджуваний економічний процес.


