
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обчислювальна імітація силового переходу у високопродуктивний станСодержание книги
Поиск на нашем сайте Розглянемо обчислювальний експеримент, спланований для дослідження енергетичного переходу економіки у високопродуктивний стан. При управлінні технічними об'єктами для зміни їхнього стану докладають силу, витрачають енергію, виконують фізичну роботу або фізичну дію. При управлінні економічними об'єктами елементарним аналогом таких зовнішніх енергетичних впливів є зміна фінансової або технологічної спроможності, пов'язаної з виробництвом товарів для збуту. Тому розглянемо модель базової економіки (3.3), (3.4), додавши до неї «штучну», суб'єктивно організовану зміну величини заощаджень власника підприємства. Таке «штучне» збільшення заощаджень власників підприємств пов'язують з цільовою емісією грошей на виробничі потреби. Емісію вважають небажаною бо вона «приводить до цінової інфляції». Якщо ж емітовані гроші спрямовують на фінансування виробництва, це веде до збільшення фінансової спроможності виробників. Додамо, що цільова емісія грошей пов'язана з дотриманням відповідної адресності, що становить окрему проблему. Розглянемо обчислювальний експеримент щодо моделювання впливу емісії грошей на перехід економіки у високопродуктивний стан. Будемо вважати, що всі параметри функцій економічної поведінки і рівнянь моделі відомі. Виберемо один параметр моделі для того, щоб з'ясувати, як його зміна позначається на динаміці розв'язків моделі. Дальше потрібно визначити, в яких межах (і з яким кроком) цей параметр змінювати , щоб модель зберігала економічний зміст (і надто не дрібнити знайдені розв'язки). Тоді, повторюючи цикл для всіх значень вибраного параметра, розв'язати моделюючі рівняння (і зберегти знайдені розв'язки). Після закінчення цього циклу – встановити залежність між зміною параметра моделі та зміною її розв'язків. В найпростішому випадку «встановлення» цієї залежності полягає у відображенні множини знайдених розв'язків з подальшим їх аналізом. У загальному випадку – необхідно встановити функціональну залежність між змінюваним параметром моделі та вибраним параметром, що описує її розв'язки. Стисло цей метод планування обчислювального експерименту описано в алгоритмі нижче. Алгоритм 3.1. Планування обчислювального експерименту для виявлення залежності розв'язків моделі від її параметра. Рівняння моделі відомі. Необхідно встановити залежність її розв'язків від одного параметра. 1. Встановити значення параметрів 2. Вибрати межі 3. Розв'язати моделюючі рівняння при поточному значенні 4. Збільшити 5. Сформувати функціональну залежність параметрів розв'язків моделі
6. Виконати аналіз знайденої функціональної залежності і розробити пропозиції щодо відповідного вдосконалення комерційного управління або державного регулювання ним.
Покажемо перехід економіки у високопродуктивний стан з допомогою емісійного збільшення заощаджень власників підприємств. Щоб зімітувати збільшення заощаджень
Зауважимо, що рівняння (3.10) відрізняється від рівняння (3.3) тим, що в ньому записано доданок Нижче подано оператори функції опису диференціальних рівнянь (3.10), (3.4), які відображають сталу емісію грошей %------ Фрагмент функції з описом СЗДР ---------------------------------------- function dydt = basem_ode (t, y) %... global emisia; % Стала емісія, значення передано через глобальний доступ dydt = [ % Рівнняння (3.10), заощадження власників підприємств y(3.2).*(n*qqq(alfa*y(3.1)./y(3.2))-(lambda+kapa)*m*fff(beta*y(3.1)./y(3.2))) + emisia
% Рівняння (3.3), ціна агрегованого товару gama*(n*qqq(alfa*y(3.1)./y(3.2))-m*fff(beta*y(3.1)./y(3.2))) ]; %------ Кінець фрагменту функції з описом СЗДР --------------------------------
Рис. 3.12. Графіки розв'язків моделі (3.10), (3.4) при різних розмірах емісії. % --------------- Програма імітації еміції грошей --------------------------- tspan = [1, 6.0]; % Проміжок часу y0 = [100; 12]; % Початкові умови figure; hold('on');
global emisia;
for iii = 1:20:150 emisia = iii; % Збільшення емісії [t,y] = ode45 (@basem_ode, tspan, y0); % Розвязуання СЗДР plot (t, y(:, 1)./y(:, 2)); % Графік капіталозабезпечення end; %--------------- Кінець програми імітації еміції грошей ---------------------- З графіків розв'язків
Рис. 3.13. Графіки капіталозабезпечення Особливо яскраво перехід економіки у високопродуктивний стан видно на графіку капіталозабезпечення З рис. 3.13 видно, що цілеспрямована емісія грошей приближає момент переходу економіки у високопродуктивний стан. Крім того, з графіків на рис. 3.12, 3.13 видно, що малі значення цілеспрямованої емісії грошей мають відносно більший вплив на перехід економіки у високопродуктивний стан, ніж більші розміри емісії. Іншими словами, ‑ при збільшенні адресної емісії ефект від неї меншає. Розв'язок базової моделі ринкової економіки, продемонстрований на рис. 3.13, показує можливість переходу у високопродуктивний стан шляхом енергетичного управління. Для здійснення такого переходу необхідні позаекономічні фактори: ідеологія економічної солідаризації, законність, покаяння. Ці висновки показують, що «для подолання економічної кризи необхідні над-економічні (позаекономічні)» заходи. Питання до параграфу 3.7 Для чого спланований обчислювальний експеримент, що імітує енергетичне переведення економіки у високопродуктивний стан? Як в базовій моделі ринкової економіки зімітувати емісію грошей для виробничих потреб підприємців? Яке можливе значення емітованих грошей для початку підприємницької діяльності? Як в дійсності в нашій країні відбувається розгортання підприємницької діяльності і в чому відмінність між цією дійсністю та припущенням про можливу адресну емісію грошей для початкуючих підприємців? Яка структура програмного забезпечення для модельного дослідження впливу адресної емісії грошей на динамічні процеси в ринковій економіці? Опишіть алгоритм обчислювального експерименту для дослідження впливу одного параметра моделі на динаміку її розв'язків. Як описати зовнішній регуляторний вплив щодо заощаджень підприємців в диференціальних рівняннях моделі ринкової економіки? Як описати зовнішній регуляторний вплив щодо заощаджень підприємців в програмного забезпечені моделі ринкової економіки? Які закономірності впливу адресної емісії грошей власникам підприємств на зміну з часом їхніх заощаджень? Які закономірності впливу адресної емісії грошей власникам підприємств на зміну з часом ціни агрегованого продукту? Які закономірності впливу адресної емісії грошей власникам підприємств на зміну з часом фінансової спроможності власників підприємств? В чому полягає тригерний характер бістабільної ринкової економіки? Як змінюється ефективність адресного імітування грошей власникам підприємств при зміні обсягів цієї емісії?
|
||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 354; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.01 с.) |

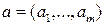 моделі, де
моделі, де 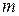 ‑ кількість параметрів. До множини параметрів
‑ кількість параметрів. До множини параметрів  належать параметри функцій економічної поведінки, параметри диференціальних рівнянь і початкові умови.
належать параметри функцій економічної поведінки, параметри диференціальних рівнянь і початкові умови.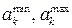 (
(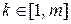 ) і крок зміни
) і крок зміни 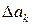 окремого параметра
окремого параметра 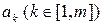 . Присвоїти початкове значення вибраного параметра
. Присвоїти початкове значення вибраного параметра 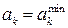 .
.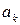 і зберегти знайдені розв'язки.
і зберегти знайдені розв'язки.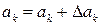 і, якщо
і, якщо 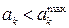 повторити пункт 3.
повторити пункт 3.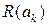 від параметра
від параметра 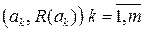 .
.
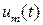 запишемо в рівнянні (3.3) доданок
запишемо в рівнянні (3.3) доданок 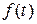 , який відображає кількість емітованих коштів, які припадають на одного підприємця за одиницю часу. Тоді рівняння (3.3) набуває такого виду.
, який відображає кількість емітованих коштів, які припадають на одного підприємця за одиницю часу. Тоді рівняння (3.3) набуває такого виду.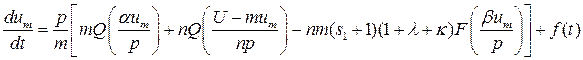 (3.10)
(3.10)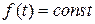 , і графіки розв'язків
, і графіки розв'язків  , отримані при різних величинах емісії.
, отримані при різних величинах емісії.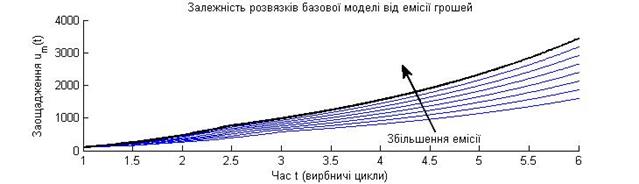
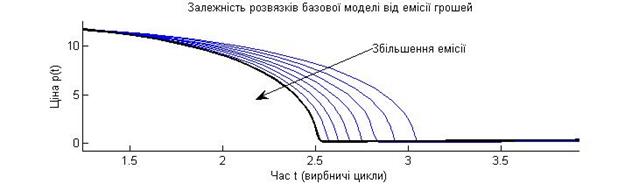
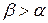 ), і обернено впливають на ціну (через збільшення пропозиції товару).
), і обернено впливають на ціну (через збільшення пропозиції товару).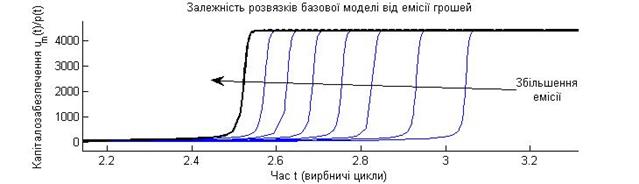
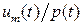 , отримані з розв'язків моделі (3.10), (3.4) при різних розмірах емісії.
, отримані з розв'язків моделі (3.10), (3.4) при різних розмірах емісії.


