
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Програмне забезпечення базової моделі ринкової економікиСодержание книги
Поиск на нашем сайте Базову модель ринкової економки описано з допомогою двох звичайних диференціальних рівнянь (3.3), (3.4) з початковими умовами (3.5). Для обчислювальних експериментів з цією моделлю необхідно розробити програмне забезпечення. Для розроблення програмного забезпечення моделі придатні універсальні мови програмування, та спеціалізовані програмні інструменти моделювання. Серед таких інструментів особливо відрізняється система інженерних розрахунків Matlab. Для розв'язування рівнянь базової моделі економіки (3.3), (3.4) необхідно застосувати обчислювальні методи розв'язування систем звичайних диференціальних рівнянь. В Matlab на основі цих методів розробленого готові програмні процедури, призначені для розв'язування систем звичайних диференціальних рівнянь. Тому для розв'язування моделюючих рівнянь достатньо викликати одну з таких готових процедур. Програма розв'язування систем звичайних диференціальних рівнянь в Matlab містить дві функції. Функцію опису системи звичайних диференціальних рівнянь і головну розв'язуючу програму, в якій описано початкові умови та виклик процедури розв'язування звичайних диференціальних рівнянь (числовими методами). Програмна функція опису системи звичайних диференціальних рівнянь приймає два параметри – масив змінних стану і час (незалежний аргумент). А повертає масив значень правих сторін системи звичайних диференціальних рівнянь (похідних від змінних стану). В головній програму розв'язування диференціальних рівнянь потрібно задати такі елементи. Описати проміжку часу
Рис. 3.8. Структура програм розв'язування звичайних диференціальних рівнянь в Matlab. В назві функції з описом системи диференціальних рівнянь прийнято вживати скорочення ODE (від англійського ordinary differential equation – звичайні диференціальні рівняння), її називають «ODE-функцією». Ця ODE-функція повертає масив похідних (правих сторін диференціальних рівнянь), його прийнято позначати dydt. Нижче подано текст ODE-функції з описом диференціальних рівнянь базової моделі (3.3), (3.4). В цій програмі присвоєно значення параметрам моделі (3.3), (3.4). Присвоєно значення масиву з 2-х елементів dydt. Перший і другий елементи масиву dydt вирахувано за відповідно формулами (3.3) і (3.4). % ------------------- ODE-функція базової моделі --------------------------- % Функція з описом рівнянь базової моделі (3.3), (3.4) function dydt = basem_ode (t, y)
n = 1; % Кількість робітників m = 1; % Кількість власників підприємств
alfa = 0.1; % Частка витрат на особисте споживання beta = 0.9; % Частка витрат на виробничі потреби lambda = 0.005; % Накладні виробничі витрати kapa = 0.01; % Податок gama = 0.05; % Параметрер інерційності ціноутворення
% Масив з двох елементів для опису системи ЗДР 2-го порядку dydt = [ % Рівнняння (3.2), заощадження власників підприємств y(3.2).*(n*qqq(alfa*y(3.1)./y(3.2)) - (lambda + kapa)*m*fff(beta*y(3.1)./y(3.2))) % Рівняння (3.3), ціна агрегованого товару gama*(n*qqq(alfa*y(3.1)./y(3.2)) - m*fff(beta*y(3.1)./y(3.2))); ]; %----------------------- Кінець ОДЕ-функції -----------------------------------
В головній програмі базової моделі економіки описано масив з двох елементів tspan. Він містить границі проміжку часу шуканого розв'язку рівнянь (3.3), (3.4). Перший елемент масиву tspan – це значення часу
% -------------------- Головна програма базової моделі (3.3), (3.4) ------------ tspan = [ 1, 12.0 ]; % Проміжок часу. y0 = [ 100; 12 ]; % Початкові умови [um(t0), p(t0)]
% Розвязування СЗДР [t,y] = ode45 (@ basem_ode, tspan, y0); % Вказівник на функцію і параметри
figure; plot (t, y(:, 1)); title(' um(t) '); figure; plot (t, y(:, 2)); title(' p(t) '); figure; plot (y(:, 1), y(:, 2)); title('Фазова траєкторія'); % -------------------------- Кінець головної програм --------------------------- На рисунках нижче зображено графіки розв'язків, знайдені з допомогою цієї програми. На рис. 3.9 зображено графіки розв'язків рівнянь (3.3), (3.4), які ілюструють перехід економіки у високопродуктивний стан.
Рис. 3.9. Графіки розв'язків базової моделі ринкової економіки при її переході у високопродуктивний стан.
На графіках
Рис. 3.10. Фазові траєкторії системи (3.3), (3.4), отримані при різних початкових умовах На рис. 3.10 зображено фазові траєкторії, знайдені з розв'язків моделі (3.3), (3.4) при різних початкових умовах Схематично фазовий портрет динамічної базової моделі ринкової економіки зображено на рис. 3.11. На цьому рисунку зображено особливі точки, особливі траєкторії і особливі області (лінії) динамічної системи (3.3), (3.4). Ці траєкторії та їх особливості (точка, лінії) визначено для динамічної системи, в якій є три рівноважні стани – стійкий низькопродуктивний (точка Тонкими стрілками позначено фазові траєкторії, які відповідають різним початковим умовам. Стрілки на них показують напрям зміщення зображуючої точки з часом. Особлива лінія – сеператриса, яка проходить через двовимірний простір (площину) На рис. 3.11 зображено лінії, де похідні рівні нулю:
Рис. 3.11. Схематичне зображення фазового портрету базової моделі ринкової економіки. Крапками на рис. 3.11 зображено лінію, яка позначає зміну координат Ілюстрація фазового портрету на рис. 3.11 прояснює, чому в базовій моделі (3.4), (3.5) застосовано лише дві динамічні змінні. Це необхідно для наочності якісного аналізу її розв'язків, показаних у двовимірній площині. Адже введення додаткових динамічних змінних ускладнює дослідження її фазового простору. Питання до параграфу 3.6 Які особливості застосування універсальних мов програмування для розроблення програмного забезпечення моделі? Які особливості застосування мов програмування для розроблення програмного забезпечення моделі? Які особливості розроблення програмного забезпечення моделі з допомогою спеціалізованих засобів моделювання? Як розв'язують системи диференціальних рівнянь з допомогою використання комп'ютерів? Що називають обчислювальними методами розв'язування диференціальних рівнянь. На яких математичних підходах ґрунтуються числові (обчислювальні) методи розв'язування систем звичайних диференціальних рівнянь? Яка структура програмного забезпечення, призначеного для розв'язування систем звичайних диференціальних рівнянь в Matlab. Якими засобами в Matlab передбачено описання систем звичайних диференціальних рівнянь? Яка в Matlab передбачено виклик бібліотечних процедур розв'язування систем звичайних диференціальних рівнянь? Які основні структурні елементи головної програми базової моделі ринкової економіки? Які основні структурні елементи програми опису системи звичайних диференціальних рівнянь? Як на розв'язках базової моделі ринкової економіки позначається момент переходу від споживання товарів першої необхідності до товарів довготривалого вжитку? Які перехідні процеси можливі в економіці, описаній її базовою моделлю? Які особливі точки і траєкторії фазового портрету базової моделі ринкової економіки. Що називають сепаратрисою фазового простору динамічної модtлі? Що називають ізоклинами фазового простору динамічної моделі. Яке економічне значення сепаратриси та ізоклин фазового простору динамічної моделі? Як геометричне місце сепаратриси та ізоклин пов'язане з стійкими і нестійкими рівноважними станами економіки, описаної її базовою моделлю? Як на фазовому портреті базової моделі економіки зобразити її енергетичне переведення у високопродуктивний стан? Як на фазовому портреті базової моделі економіки зобразити її параметричне переведення у високопродуктивний стан?
|
||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 419; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.009 с.) |

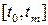 числового розв'язування диференціальних рівнянь. Задати початкові умови розв'язку (тобто – значення шуканого розв'язку в момент часу
числового розв'язування диференціальних рівнянь. Задати початкові умови розв'язку (тобто – значення шуканого розв'язку в момент часу  ). Викликати процедуру розв'язування диференціальних рівнянь, явно вказавши в ній такі параметри: назву програмної функції з описом диференціальних рівнянь, початкові умови та проміжок розв'язування. Процедура розв'язування диференціальних рівнянь (першими двома параметрами) повертає масив значень аргументу на
). Викликати процедуру розв'язування диференціальних рівнянь, явно вказавши в ній такі параметри: назву програмної функції з описом диференціальних рівнянь, початкові умови та проміжок розв'язування. Процедура розв'язування диференціальних рівнянь (першими двома параметрами) повертає масив значень аргументу на 
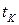 у кінцевому вузлі розв'язування диференціальних рівнянь. Початкові умови
у кінцевому вузлі розв'язування диференціальних рівнянь. Початкові умови  ,
,  занесено в масив з двох елементів y0. Розв'язок знайдено з допомогою процедури ode45. Цей розв'язок міститься у дискретній функціональній залежності. Аргументи
занесено в масив з двох елементів y0. Розв'язок знайдено з допомогою процедури ode45. Цей розв'язок міститься у дискретній функціональній залежності. Аргументи 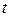 цієї залежності містяться в одновимірному масиві t, відповідні значення функцій
цієї залежності містяться в одновимірному масиві t, відповідні значення функцій 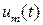 ,
, 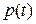 містяться у двовимірному масиві y. Графіки знайдених розв'язків
містяться у двовимірному масиві y. Графіки знайдених розв'язків 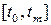 відображено з допомогою функцій plot.
відображено з допомогою функцій plot.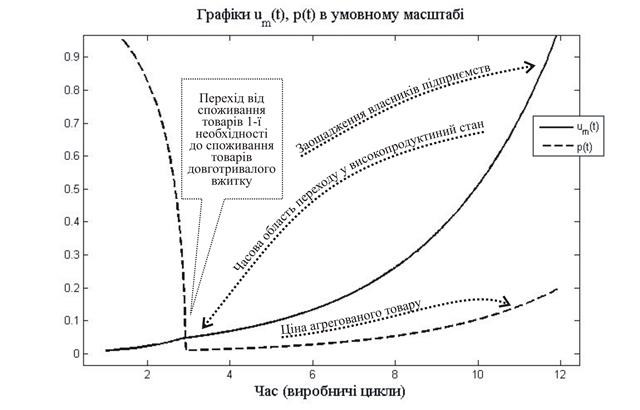
 потрапляє в область вгину
потрапляє в область вгину 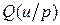 .
.
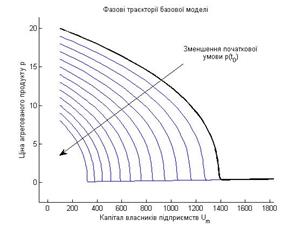
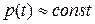 , потім – рухається вздовж неї. Рисунки 3.10 ілюструють фрагмент загального фазового портрету динамічної системи (3.3), (3.4). На основі детального аналізу розв'язків базової моделі ринкової економіки встановлено фазовий портрет системи (3.3), (3.4).
, потім – рухається вздовж неї. Рисунки 3.10 ілюструють фрагмент загального фазового портрету динамічної системи (3.3), (3.4). На основі детального аналізу розв'язків базової моделі ринкової економіки встановлено фазовий портрет системи (3.3), (3.4). ), нестійкий низькопродуктивний (точка
), нестійкий низькопродуктивний (точка  ), стійкий високопродуктивний (
), стійкий високопродуктивний (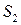 ). Точки
). Точки 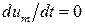 ;
; 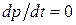 .
. , ділить його на дві окремі області. В них є стійкі положення рівноваги
, ділить його на дві окремі області. В них є стійкі положення рівноваги 
 при силовому (енергетичному) переведенні зображуючої точки з області притягання низькопродуктивного стану (точки
при силовому (енергетичному) переведенні зображуючої точки з області притягання низькопродуктивного стану (точки 


