
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виробнича функція, функція споживанняСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Виробнича функція, функція споживання Функції економічної поведінки Господарювання пов'язане з перетворенням матеріальних предметів, фізичних і біологічних. Людина працює і організовує господарську діяльність щоб отримати необхідні матеріальні речі: їжу, тепло, одяг, побутові предмети. В цьому сенсі господарські відносини «залежать від природних законів». Наприклад, економічна ефективність «залежить» від фізичного коефіцієнта корисної дії застосованого обладнання або від біологічної урожайності. Крім того, на господарських відносинах позначаються соціальні фактори – культура, психологія, ідеологія, історичні обставини, а також – право, мораль і релігія. За таких умов людина вибирає той чи інший вид господарської діяльності. Такий вільний господарський вибір, обмежений природними законами, регульований суспільними нормами, називають економічною поведінкою. Економічна поведінка має певні властивості. Наприклад, в українській традиції економічну поведінку виховують, протиставляючи працьовитість й лінивство. З християнського погляду ревність у праці, намагання працювати якнайкраще є чеснотою і святим обов'язком. Економічна поведінка та її усвідомлення також є різним в окремих країнах. Так, в нашій країні економічної поведінки навчають прислів'я («біда навчить, як на світі жить», «де літуєш, там зимуй», «що влітку під ногами, взимку – під зубами»). В англійській ‑ уявні економічні експерименти. «Економічна поведінка» є категорією, зручною з погляду інженерії отримання знань. Справді, вона стосується суб'єкта виробничої діяльності. Її легко «виявити за емпіричними спостереженнями», кількісно описати з допомогою математичних співвідношень. Функцію, яка відображає економічну поведінку учасника господарських відносин, називають функцією економічної поведінки. Аргументи цієї функції позначають діючі фактори, якими управляє учасник економіки. Значення функції поведінки позначає результат цього управління. Функція економічної поведінки залежить від природних і соціальних законів. На ній позначаються впливи національних, історичних, соціальних, культурних, ідеологічних обставин.
Функції економічної поведінки описують «миттєву реакцію» на дію вхідного впливу (аргументу функції). Найчастіше в моделюванні економіки застосовують функції поведінки, які описують виробництво і споживання. Функції економічної поведінки є предметом дослідження математичної економіки. Для ідентифікації функції економічної поведінки необхідно встановити емпіричне узагальнення, яке описує поведінку учасника (суб'єкта) економіки, вибрати значення функції та її аргументи, встановити якісну залежність значень функції від її аргументів, вибрати математичний вираз, який відповідає цій залежності, встановити значення параметрів, котрі входять в цей вираз. При цьому необхідно брати до уваги область прийнятних значень аргументів та функції (тобто – вибрати області визначення і значень). Функція економічної поведінки є найпростішою моделлю економічного об'єкта. Функції економічної поведінки застосовують в більш складних моделях.
Функції економічної поведінки описують закономірності, які стосуються окремого учасника економіки. Це зручний, але не єдиний спосіб математичного опису економічних закономірностей. Інший підхід (який не є альтернативним), ґрунтується на встановленні економічних закономірностей, якими зв'язані різні учасники економіки. Зауважимо, що (всяка неперервна) функція може бути записана диференціальними рівнянням, яке має розв'язок, котрий дорівнює цій функції. Тому функції економічної поведінки замінюють на диференціальні рівняння. Функції економічної поведінки ‑ це категорія інженерії знань. Їх зручно застосовувати для вивчення сучасної економіки. Питання до параграфу 2.1 Назвіть приклади, в яких виявляється залежність господарювання від природних законів та норм регулювання, притаманних людині, суспільству. Які основні позасвідомі імпульси впливають на економічні дії людини? Назвіть приклади, які показують залежність господарських дій окремо від природних і «соціальних законів» та приклади, «використання» цих законів в економічних інтересах. Які основні напрями впливу Християнства на економічну поведінку людини? Як пов'язаний вільний вибір, здатність активно діяти та господарська поведінка? В чому відмінність та схожість господарської поведінки індивіда, колективу, людства? Доведіть, що за «інтересами виробничої системи» криються індивідуальні мотиви господарської поведінки. Назвіть приклади деструктивної економічної поведінки індивіда, групи, глобального економічного утворення. Що таке економічна деструктивність? Як пов'язані агресія некрофільства, садизму, нарцисизму з економічною поведінкою? Назвіть вияви різниці між життєствердною та руйнівною економічно поведінкою. В чому різниці між економічною поведінкою громадян західних країн 19 століття і економічною поведінкою, що відповідає ідеології споживання? Який зміст категорій «бути чи мати» щодо самопредставлення людини? Назвіть десять українських (російських, польських) прислів'їв або приповідок, що описують економічну поведінку. Чому категорія «економічна поведінка» не має суттєвого значення в гуманітарних підходах до вивчення економіки? Який роль категорії «економічна поведінка» в інженерії знань? Що таке функція економічної поведінки? Як математичною функцією відобразити економічну закономірність? Які функції економічної поведінки широко застосовують в моделюванні економіки? Яка низка пізнавальних дій приводить до застосування функції економічної поведінки при дослідженні економіки? З якою практичною метою встановлюють функції економічної поведінки? Як представити функцію економічної поведінки з допомогою диференціальних рівнянь? Виробнича функція Для моделювання виробництва товару застосовують виробничі функції. Виробничою функцією називають функціональну залежність, яка відображає зв'язок між кількістю ресурсів, вкладених (використаних, витрачених, застосованих) при виробництві, та кількістю продукту, отриманого в результаті цього. Тобто, виробнича функція є «математичним аналогом» виробничого підприємства, на вході якого – ресурси, а на виході ‑ «готова продукція». Аргументи виробничої функції описують ресурсів, використані в ході виробництва. Значення виробничої функції – це кількість виробленої продукції.
Виробництво (одиниці товару) відбувається не миттєво, а протягом якогось фізичного (календарного) проміжку часу. Тому виробничу функцію записують для проміжку часу, протягом якого відбувається розхід ресурсів і створення відповідної кількості товарів. Аргументами і значеннями у виробничій функції є величини, які описують зміну кількості товару і ресурсу (матеріального, трудового, фінансового) за проміжок часу. За аналогією з течією рідини таку зміну кількості ресурсу за одиницю часу називають розходом, або швидкістю розходу ресурсу. Його вимірюють в кількості одиниць ресурсу за одиницю часу Виробничу функцію зручно вважати неперервною функцією неперервних аргументів. Це дає підстави застосовувати її для опису миттєвого зв'язку між аргументами (розходом ресурсів) й значеннями (кількістю товару) в диференціальних або інтегральних рівняннях. Позначимо
Матеріальні і фінансові види ресурсів мають відповідно фізичні й економічні особливості їх розходу й використання. Ці особливості позначаються на властивостях виробничої функції. Як зазначалося, ці властивості є предметом вивчення математичної економіки. Проте, для дослідження сучасної ринкової економіки зручніше застосовувати інші пізнавальні підходи. В детально розроблених імітаційних моделях аргументами виробничої функції вибирають розхід матеріалів, комплектуючих, електроенергії, палива для транспорту, коштів на оплату праці та інших. В таких випадках виробнича функція імітує реальні закономірності виробничого процесу. Проте, для моделювання ринкової економіки важливо застосувати виробничі функції, які розкривають найзагальніші економічні закономірності, уникаючи несуттєвої деталізації.
Розглянемо приклад виробничої функції, взятий з оповідання І. Франка, в якому описано виробництво березових мітел. Майстер заготовляє в лісі різки берези. Відповідно до їх кількості ‑ виготовляє мітли. Кількість виготовлених мітел залежить від кількості заготовлених прутиків. Цю залежність описує виробнича функція. Аргументами цієї функції є кількість (заготовлених заздалегідь) різок берези. Значенням цієї функції є кількість виготовлених віників. Параметром такої функції є кількість різок, необхідних для виробництва одного віника. Словами (вербально) функцію економічної поведінки виробника мітел описує таке твердження: кількість мітел, які робить майстер прямо пропорційна кількості використаних різок. Це твердження легко відобразити математичним співвідношенням. Знехтуємо часом роботи, знехтуємо заготівлею різок. Нехай
де В першому наближенні аргументом виробничої функції
Аргументами виробничої функції також застосовують фондоозброєність. Для дослідження найзагальніших економічних процесів, що відбуваються в сучасній економіці, виробничу функцію зручно записати через залежність від капіталозабезпечення на одиницю часу на одне робоче місце на одиницю вартості виробленої продукції:
де
Значеннями цієї виробничої функції
є кількість товару, виготовленого за одиницю часу (за виробничий цикл ‑ один період повторення виробництва одного і того ж товару). Аргументом цієї функції капіталозабезпечення на одне робоче місце, на одиницю часу. Розглянемо властивості виробничої функції Якщо на виробництво не витрачають фінансових ресурсів тоді (в умовах товарного виробництва) немає виробленої продукції. Отже, Дійсна функція Виробнича функція Зауважимо, що у випадку великих складальних виробництв, зайнятих випуском одиничних виробів, виробнича функція Виробнича функція
Тобто, виробнича функція зростає не швидше прямої лінії. Ця властивість випливає з емпіричних спостережень. Справді, припустимо, що власник підприємства при капіталовитратах Виробнича функція
Емпірично відомо, що Додамо, що інколи необхідно брати до уваги таку властивість. Швидкість зростання функції
Справді, збільшення фінансових витрат відбувається при одночасному збільшенні виробництва. При великих розмірах виробництва витрати на управління необмежено зростають, що зменшує витрати на випуск продукції припиняють зростати. Втім, ця властивість проявляється лише при таких великих розмірах виробництва. Описані вище властивості виробничої функції є типовими висновками математичної економіки. Проте, вони потребують уточнень. Хоч описані властивості математично обґрунтовані, вони не стосуються економічних об'єктів зі специфічними властивостями. Розглянемо декілька характерних видів виробничих функцій.
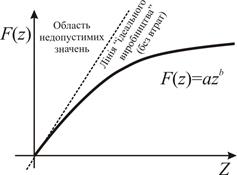
Рис. 2.1. Графіки виробничих функцій різних локальних економічних об'єктів.
На рис. 2.1а зображено графік виробничої функції, яка всюди зростає. Такі виробничі функції відповідають середнім підприємствам, на яких відбувається вдосконалення (підвищення продуктивності) виробництва. На рис. 2.1б зображено графік обмеженого виробничої функції. Такі виробничі функції відповідають середнім підприємствам, які не впроваджують нових технологій. Графік на рис. 2.1в зображує виробничу функцію малого індивідуального підприємства. При капіталозабезпеченні, меншому за На рисунку 2.1г зображено графік виробничої функції виробництва агрегованого продукту в країнах колишнього Радянського Союзу. На цих підприємствах збереглися виробничі фонди, завантажені частково. Їх неповне завантаження імітує відрізок лінійного зростання виробничої функції на рис. 1.г. Повне завантаження виробничих фондів таких підприємств відображає відрізок постійного значення Виробнича функція має близьку фізичну аналогію. Якщо аргумент виробничої функції – це фінансові затрати (розхід енергії), а її значення – це користь (виконана робота), тоді фізичним аналогом виробничої функції є функція корисної дії механізму в залежності від потужності його роботи:
де Типовий графік виробничої функції «надзвичайно великого економічного об'єкта» зображено на рисунку 2.2. Зауважимо, що так же виглядає графік функції корисної дії фізичного механізму. Спад функції
Рис. 2.2. Графік виробничої функції «надзвичайно великого» об'єкта.
Аналогія між виробничою функцією та функцією корисної дії показує, що обмеження зростання Описані вище властивості виробничих функцій встановлено на основі якісного аналізу відповідних економічних об'єктів. Це один з способів встановлення виробничих функцій. Застосовують й інший підхід. Параметри виробничої функції визначають за відомими значеннями капіталозабезпечення та обсягів виробництва. Ці відомі значення називають експериментальними даними (бо вони взяті з «експериментального вимірювання» ‑ спостережень за об'єктом дослідження), або даними звітності (бо вони взяті з періодичної звітності підприємства). Визначення параметрів функції економічної поведінки на основі відомих її значень називають ідентифікацією її параметрів, або ідентифікацією функцій економічної поведінки. Додамо, що для ідентифікації параметрів ції функції спершу обхідно вибрати алгебричний вираз, який відображає досліджувану економічну тенденцію. Розглянемо ідентифікацію параметрів виробничої функції
де
Рис. 2.3. Ілюстрація до степеневої апроксимації експериментальних значень виробничої функції.
В дискретній залежності (2.4) під моментами часу Пара величин Задача ідентифікації виробничої функції виробничої функції полягає в тому, щоб за даними Задачами відновлення називають задачі, в яких за відомими розв'язками необхідно встановити рівняння. Задача відновлення виробничої функції власне полягає в тому, щоб за даними (2.4) встановити функцію Повернемося до визначення параметрів виробничої функції. Апроксимуємо
в якій невідомі параметри
Це
яку важко розв'язувати числовими методами. Інший підхід ґрунтується на усередненні явних розв'язків пари рівнянь (2.6), записаних для двох суміжних вузлів:
які мають явний розв’язок
де З нього знаходимо усереднені значення параметрів:
Як видно з поданих прикладів – ідентифікація виробничої функції за експериментальними даними потребує розв'язування складних обчислювальних задач. Це суттєво утруднює застосування такого підходу в задачах моделювання економіки.
Тому надалі для опису залежності кількості виробленого продукту від капіталозабезпечення будемо застосовувати функцію В сучасних країнах колишнього виробничі фонди, створені при плановій економіці, використовують не на повну потужність, а частково, відповідно до наявного капіталозабезпечення. А також немає оновлення виробничих фондів. За таких умов виробнича функція має такі властивості. При малому капіталозабезпеченні (від нуля до межі, поки виробничі фонди не завантажені на повну потужність) виробнича функція прямо залежить від капіталозабезпечення. При великому кпіталозабезпеченні (коли виробничі фонди звантажені на повну потужність) кількість виробленого продукту не залежить від капіталозабезпечення. Таку залежність описує функція:
де В моделюванні економіки виробничу функцію застосовують двома способами. По-перше, на її властивості посилаються, виконуючи якісний аналіз розв'язків моделі. По-друге, на основі математичної виробничої функції розробляють відповідну програмну функцію (програмну процедуру). Її застосовують як структурний елемент програмного забезпечення моделі з метою виконання з ними обчислювальних експериментів. Розглянемо програмну мовою Matlab для виробничої функції
%- Функція fff --------------------------------------------------------- function ret_value_fff = fff (rrr) % Прогама виробничої функції F(z) % function ret_value_fff = fff (rrr) % Вхідні параметри: % rrr - капiталозабезпечення, rrr >= 0. % Вихідні параметри: % ret_value_fff - кількість виобленого проду кту % Внутрішні параметри: % fmax - максимальна кілікість продукту, % виробленого за одиницю часу % aaa - параметер, що має значення капіталовівдачі %------------------------------------------------------------------- % function ret_value_fff = fff (rrr) % Виробництво агрегованого продукту без оновлення виробничих фондів %-------------------------------------------------------------------
% function ret_value_fff = fff (rrr) aaa = 3.7; % Капіталовіддача fmax = 1500; % Максимальна кількість продукту
q1_tmp = rrr.*aaa; % Лінійне зростання виробничої функції q2_tmp = ones (size(rrr)).*fmax; % Максимальне значення виробничої функції
% Вирахуання за формулою (2.7) ccc1 = (q1_tmp <= q2_tmp).*q1_tmp; ccc2 = (q1_tmp > q2_tmp).*q2_tmp; ret_value_fff = ccc1 + ccc2; %- Кінець функції fff ---------------------------------------------------
Звертання до програми fff() виробничої функції продемонстровано з на прикладі виклику функції plot(), яка виводить графік в прямокутній системі координат. %------------------------------------------------------------------------------- zzz = 0: 1: 600; % аргумент r=[0, 600] hndl = plot(zzz, fff(zzz)); % графік функції F(z) на [0, 600] %-------------------------------------------------------------------------------
Параметр |
||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 559; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.013 с.) |

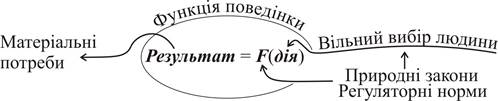


 . В комерційній практиці одиницями часу вибирають переважно календарні його проміжки, пов'язані з пануванням та звітністю. Проте, для моделювання економіки зручніше вибирати за одиницю часу тривалість виготовлення одиниці товару.
. В комерційній практиці одиницями часу вибирають переважно календарні його проміжки, пов'язані з пануванням та звітністю. Проте, для моделювання економіки зручніше вибирати за одиницю часу тривалість виготовлення одиниці товару.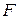 ‑ кількість товару (в натуральних одиницях);
‑ кількість товару (в натуральних одиницях); 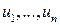 ‑ обсяги ресурсів, витрачених за одиницю часу, де
‑ обсяги ресурсів, витрачених за одиницю часу, де 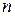 ‑ кількість видів ресурсів. Тоді кількість товару, виробленого за одиницю часу:
‑ кількість видів ресурсів. Тоді кількість товару, виробленого за одиницю часу: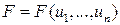 .
.
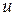 ‑ кількість різок; для виготовлення однієї мітли потрібно
‑ кількість різок; для виготовлення однієї мітли потрібно  різок. Тоді:
різок. Тоді: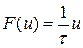 , (2.1)
, (2.1)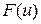 ‑ кількість мітел, які вироблено з
‑ кількість мітел, які вироблено з 
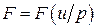 ,
,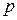 ‑ ціна товару; величина
‑ ціна товару; величина  – відображає фінансову спроможність власника підприємства щодо виробництва продукції ‑ це капіталозабезпечення на одиницю вартості виробленої продукції, або відносне капіталозабезпечення. Позначимо його
– відображає фінансову спроможність власника підприємства щодо виробництва продукції ‑ це капіталозабезпечення на одиницю вартості виробленої продукції, або відносне капіталозабезпечення. Позначимо його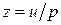 , (2.2)
, (2.2)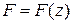 (2.3)
(2.3) , залежної від фінансової спроможності власника підприємства s, яка виражена виробничими капіталовитратами за одиницю часу на одне робоче місце на одиницю ціни товару. Ці властивості встановимо на основі аналізу емпіричних закономірностей економічної поведінки виробників (власників підприємств) для економічних об'єктів «середнього розміру». Додамо, що вони не стосуються малих виробників (індивідуальних виробництв) та виробництв глобального масштабу.
, залежної від фінансової спроможності власника підприємства s, яка виражена виробничими капіталовитратами за одиницю часу на одне робоче місце на одиницю ціни товару. Ці властивості встановимо на основі аналізу емпіричних закономірностей економічної поведінки виробників (власників підприємств) для економічних об'єктів «середнього розміру». Додамо, що вони не стосуються малих виробників (індивідуальних виробництв) та виробництв глобального масштабу.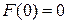 .
.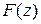 дійсних значень визначена на додатній півосі. Справді, відомо, що деякі економічні величини допускають від’ємні й додатні значення. Це, наприклад, ‑ величина заборгованості. Проте, кількість коштів, вкладених у виробництво (не залежно від джерела фінансування), завжди є невід’ємною величиною. Зокрема, це однаково стосується фінансування виробництва з власних і позичкових джерел. Отже,
дійсних значень визначена на додатній півосі. Справді, відомо, що деякі економічні величини допускають від’ємні й додатні значення. Це, наприклад, ‑ величина заборгованості. Проте, кількість коштів, вкладених у виробництво (не залежно від джерела фінансування), завжди є невід’ємною величиною. Зокрема, це однаково стосується фінансування виробництва з власних і позичкових джерел. Отже, 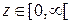 .
.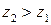 , тоді
, тоді 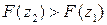 . Це відповідає умові зростання функції
. Це відповідає умові зростання функції 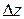 , тоді на відрізку
, тоді на відрізку 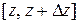 виробнича функція залишається сталою. Втім, при розробці динамічних моделей таким обмеженням нехтують. Це не призводить до суттєво погіршення моделі, адже вважається, що за одиницю часу на одиницю витрачених ресурсів виробляють не цілий виріб, а його частину.
виробнича функція залишається сталою. Втім, при розробці динамічних моделей таким обмеженням нехтують. Це не призводить до суттєво погіршення моделі, адже вважається, що за одиницю часу на одиницю витрачених ресурсів виробляють не цілий виріб, а його частину. .
. виробляє
виробляє 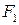 продукції. Якщо відкинути загальні накладні витрати (організація виробництва, брак, відходи, помилки, ліквідація аварій, технічне обслуговування, крадіжки, природне псування продукції, зношення обладнання, розсіяння енергії тощо), тоді всі капіталовитрати
продукції. Якщо відкинути загальні накладні витрати (організація виробництва, брак, відходи, помилки, ліквідація аварій, технічне обслуговування, крадіжки, природне псування продукції, зношення обладнання, розсіяння енергії тощо), тоді всі капіталовитрати  , де k – ідеальна ефективність використання капіталу. Оскільки в дійсності існують загальні накладні витрати, тому на виробництво продукції припадає лише частина фінансових витрат
, де k – ідеальна ефективність використання капіталу. Оскільки в дійсності існують загальні накладні витрати, тому на виробництво продукції припадає лише частина фінансових витрат 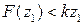 . Оскільки
. Оскільки 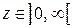 .
.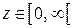 . Справді, нехай при капіталовкладеннях
. Справді, нехай при капіталовкладеннях 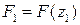 продукції. Розмір загальних накладних витрати
продукції. Розмір загальних накладних витрати  . Емпірично відомо, що розширення виробництва веде до прискореного збільшення накладних витрат. Це пов’язано з тим, що кожна нова виробнича одиниця потребує більше накладних витрат, чим остання попередня. Це призводить до того, що при збільшенні z величина
. Емпірично відомо, що розширення виробництва веде до прискореного збільшення накладних витрат. Це пов’язано з тим, що кожна нова виробнича одиниця потребує більше накладних витрат, чим остання попередня. Це призводить до того, що при збільшенні z величина 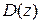 росте швидше за величину
росте швидше за величину  . Звідси
. Звідси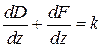 ;
; 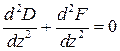 .
.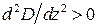 , адже, як зазначалося, збільшення виробництва веде до прискореного росту загальних виробничих накладних витрат. Тому
, адже, як зазначалося, збільшення виробництва веде до прискореного росту загальних виробничих накладних витрат. Тому 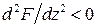 , тобто
, тобто  прямує до нуля.
прямує до нуля.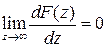 .
. a
a  б
б  в
в 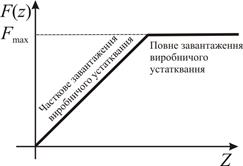 г
г підприємець не може виробляти товару, тому
підприємець не може виробляти товару, тому  при
при 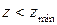 . Тут величина
. Тут величина 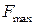 .
.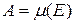 ,
, ‑ корисна робота (аналог кількості продукції);
‑ корисна робота (аналог кількості продукції); 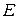 ‑ витрачена енергія (аналог витрат капіталу);
‑ витрачена енергія (аналог витрат капіталу);  ‑ функція корисної дії. Для простих механізмів (важеля, домкрата, блока) функція корисної дії зводиться до добутку
‑ функція корисної дії. Для простих механізмів (важеля, домкрата, блока) функція корисної дії зводиться до добутку  , де
, де 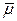 ‑ коефіцієнт корисної дії. Для складних механізмів – двигунів, транспортних засобів функція корисної дії має центральний максимум, який відповідає так званому «номінальному навантаженню» механізму («номінальній потужності» експлуатації) з максимальним коефіцієнтом корисної дії. Для транспортних засобів, (технологічних ліній) таку «номінальну потужність» виражають через найкращу рекомендовану швидкість руху (інтенсивність експлуатації).
‑ коефіцієнт корисної дії. Для складних механізмів – двигунів, транспортних засобів функція корисної дії має центральний максимум, який відповідає так званому «номінальному навантаженню» механізму («номінальній потужності» експлуатації) з максимальним коефіцієнтом корисної дії. Для транспортних засобів, (технологічних ліній) таку «номінальну потужність» виражають через найкращу рекомендовану швидкість руху (інтенсивність експлуатації).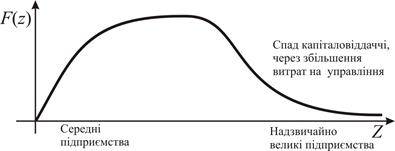
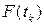 і купівельної спроможності
і купівельної спроможності 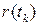 в моменти часу
в моменти часу  ,
,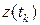 (
( ). (2.4)
). (2.4)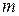 ‑ кількість таких відомих даних. Необхідно встановити параметри функції
‑ кількість таких відомих даних. Необхідно встановити параметри функції 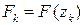 для всіх
для всіх 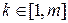 . Зауважимо, що таку задачу називають задачею апроксимації, або задачею наближення. Схематичну ілюстрацію до цієї задачі показано на рис. 2.3.
. Зауважимо, що таку задачу називають задачею апроксимації, або задачею наближення. Схематичну ілюстрацію до цієї задачі показано на рис. 2.3.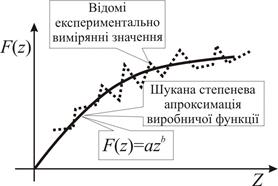
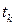 економісти-практики розуміють «звітні періоди» (місяці, квартали, роки). В динамічному моделюванні ці моменти часу позначають час у його фізичному сенсі, виміряний в довільних одиницях. Вибір одиниць часу впливає на розв'язки рівнянь моделей, а позначається лише на масштабі відображення даних. Проте, в моделях зручно використовувати одиницю часу, яка прив'язана до тривалості виробничого циклу (тривалості виготовлення одиниці товару). Такий проміжок часу має неоднакову фізичну тривалість «в секундах», в фізичному розумінні. Так виникає «власний час» економічного об'єкта, що має термінологічну аналогію з таким же поняттями фізичної теорії відносності. В багатьох галузях економіки (насамперед – у сільському господарстві) тривалість виробничого циклу «точно» дорівнює року. Така прив'язаність тривалості виробничого циклу до астрономічної величини не є «збігом обставин». Адже Сонце – єдине джерело енергії Біосфери, в якій відбувається фотосинтез продуктів харчування, які необхідні для існування всіх інших форм господарювання.
економісти-практики розуміють «звітні періоди» (місяці, квартали, роки). В динамічному моделюванні ці моменти часу позначають час у його фізичному сенсі, виміряний в довільних одиницях. Вибір одиниць часу впливає на розв'язки рівнянь моделей, а позначається лише на масштабі відображення даних. Проте, в моделях зручно використовувати одиницю часу, яка прив'язана до тривалості виробничого циклу (тривалості виготовлення одиниці товару). Такий проміжок часу має неоднакову фізичну тривалість «в секундах», в фізичному розумінні. Так виникає «власний час» економічного об'єкта, що має термінологічну аналогію з таким же поняттями фізичної теорії відносності. В багатьох галузях економіки (насамперед – у сільському господарстві) тривалість виробничого циклу «точно» дорівнює року. Така прив'язаність тривалості виробничого циклу до астрономічної величини не є «збігом обставин». Адже Сонце – єдине джерело енергії Біосфери, в якій відбувається фотосинтез продуктів харчування, які необхідні для існування всіх інших форм господарювання.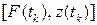 , де
, де  відображає точку на площині (в двовимірному просторі), з координатами
відображає точку на площині (в двовимірному просторі), з координатами 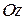 , на якій лежать аргументи виробничої функції) та
, на якій лежать аргументи виробничої функції) та 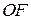 , на якій лежать значення виробничої функції). Всі
, на якій лежать значення виробничої функції). Всі  , де
, де  ‑ відповідно найменше і найбільше значення аргументу зі всіх
‑ відповідно найменше і найбільше значення аргументу зі всіх  ,
, 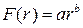 , (2.5)
, (2.5)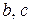 степеневої функції описують відповідно обсяг виробництва і схильність до його збільшення при зростанні капіталозабезпечення. Параметри
степеневої функції описують відповідно обсяг виробництва і схильність до його збільшення при зростанні капіталозабезпечення. Параметри 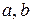 ідентифікованих функцій поведінки мають відображати реальне виробництво протягом часу
ідентифікованих функцій поведінки мають відображати реальне виробництво протягом часу  . Підставляючи значення (2.4) в рівняння (2.5), отримуємо умову, якій мають відповідати параметри виробничої функції
. Підставляючи значення (2.4) в рівняння (2.5), отримуємо умову, якій мають відповідати параметри виробничої функції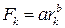 (
(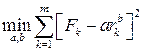 ,
, (
( ),
),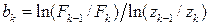 ;
;  ; (
; ( ‑ кількість пар значень
‑ кількість пар значень  ;
; 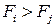 .
. ;
; 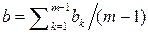 .
.
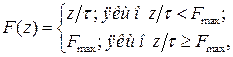 (2.7)
(2.7) . Тому, підставляючи функцію
. Тому, підставляючи функцію  виробничої функції (2.7) має сенс середньої капіталовіддачі. Параметр
виробничої функції (2.7) має сенс середньої капіталовіддачі. Параметр 


