
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математичні методи наукового дослідження: аналітичні методи; математичне моделюванняСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Аналітичні методи дослідження (елементарна математика, диференціальні й інтегральні рівняння, варіаційне обчислення та інші розділи вищої математики), використовувані для вивчення безперервних детермінованих процесів. За допомогою аналітичних методів дослідження встановлюють математичну залежність між параметрами моделі. Ці методи дозволяють глибоко й всебічно вивчити досліджувані процеси, встановити точні кількісні зв'язки між аргументами й функціями, глибоко проаналізувати досліджувані явища. Математична модель може бути подана у вигляді функції, рівняння, у вигляді системи рівнянь, диференціальних або інтегральних рівнянь. Такі моделі звичайно містять велику кількість інформації. Характерною рисою математичних моделей є те, що вони можуть бути перетворені за допомогою математичного апарату. Так, наприклад, функції можна досліджувати на екстремуми; диференціальні або інтегральні рівняння можна розвязувати. При цьому дослідник одержує нову інформацію про функціональні зв'язки й властивості моделей. Використання математичних моделей є одним з основних методів сучасного наукового дослідження, але він має істотні недоліки. Для того щоб знайти особливе рішення, властиве лише даному процесу, необхідно задати умови й обмеження. Встановлення граничних умов вимагає проведення достовірного досліду й ретельного аналізу експериментальних даних. Неправильне прийняття граничних умов приводить до того, що піддається теоретичному аналізу не той процес, що планується, а видозмінений. Крім зазначеного недоліку аналітичних методів, у багатьох випадках відшукати аналітичні значення з урахуванням визначених умов, що найбільше реально відображають фізичну сутність досліджуваного процесу, або взагалі неможливо або надзвичайно важко. Іноді, досліджуючи складний фізичний процес при ретельно обґрунтованих обмежуючих умовах, спрощують вихідні диференціальні рівняння через неможливість або надмірну громіздкість їх розвязання, що спотворює його фізичну сутність. Таким чином, дуже часто реалізувати аналітичні залежності складно. Експериментальні методи дозволяють глибоко вивчити процеси у межах точності техніки експерименту й сконцентрувати увагу на тих параметрах процесу, які становлять найбільший інтерес. Однак результати конкретного експерименту не можуть бути поширеними на інший процес, навіть близькими за фізичною сутністю, тому що результати будь-якого експерименту відображають індивідуальні особливості лише досліджуваного процесу. З досвіду ще неможливо остаточно встановити, які з параметрів впливають на хід процесу і як буде проходити процес, якщо змінювати різні параметри одночасно. При експериментальному методі кожний конкретний процес повинен бути дослідженим самостійно. Таким чином, і аналітичні, і експериментальні методи мають свої переваги й недоліки, які нерідко утруднюють ефективне вирішення практичних завдань. Тому надзвичайно плідним є сполучення позитивних сторін аналітичних і експериментальних методів дослідження. 2. Метод формалізації – це вивчення об’єктів шляхом відображення їх змісту, структури, форми чи функціонування у знаковому вигляді, з допомогою штучних мов (знакових систем). В останньому аспекті він близький до методу моделювання, бо одним із видів методу формалізації є математичне моделювання (воно з успіхом включається у формально-знакове моделювання). Крім математичної формалізації, існує логіко-математична, особливо при вивченні структури понять і у логічному вимірі, а також знакова формалізація – за допомогою штучної мови символів (значків) і операцій з ними. Найповніше, особливо починаючи з 60-х років, використовується математична формалізація. У широкому розумінні – це застосування в науці принципів і положень, методологічного і формального апарату, власне, математики і математичної логіки, особливо математичних прийомів обробки кількісної інформації. Застосування математичних засобів обробки фактичних даних з метою виведення емпіричних закономірностей у вигляді математичних формул, рівнянь і нерівностей чи їх систем. Математичне моделювання – це створення математичної моделі і експериментування з нею. Класичним прикладом в економіці є відома формула (модель) попиту на товар: Q=f(P), (4.1) де Q – обсяг попиту на певний товар, або максимальна кількість одиниць товару, який готові придбати покупці за певну ціну; Р –ціна цього товару. Якщо у цій моделі змінювати значення ціни товару (це і буде експеримент), то і вихідне значення (обсяг попиту) теж буде змінюватися. Отже, отримуватимемо різні обсяги продукції, що зможуть придбати покупці за певною ціною. Формалізація (математизація) дає змогу використовувати у дослідженнях інформаційні системи (ІС) і відповідно інформаційні дослідницькі технології. 3. Ймовірнісно-статистичні методи дослідження (статистика й теорія ймовірностей, дисперсійний і корреляційний аналізи, теорія надійності, метод Монте-Карло та ін.) використовуються для вивчення випадкових процесів – дискретних і безперервних. Досить часто застосовують методи теорії ймовірностей і математичної статистики в теорії надійності, які широко використовуються в різних галузях науки й техніки. Основним завданням теорії надійності є прогнозування (пророкування з тією або іншою ймовірністю) різних показників - безвідмовної роботи, терміну служби й т.д. Вона пов'язана зі знаходженням імовірностей. Параметрична кореляція (коефіцієнт кореляції Пірсона) Передумови: · Усі спостереження взаємно незалежні. · Спостереження мають нормальний закон розподілу. Опис методу Значення коефіцієнта кореляції обчислюється за формулою 4.2:
Коефіцієнт кореляції показує щільність лінійного зв'язку між двома вибірками випадкових величин. Його значення змінюється від -1 (рис. 4.1, rxy = -0,8), що відповідає зворотному зв'язку, до +1 (рис. 4.2, rxy = 0,8), що відповідає прямо пропорційному зв'язку (значення 0 означає відсутність зв'язку - рис. 4.3).
Рис. 4.1 Приклад зворотної кореляційної залежності
Рис. 4.2 Приклад прямої кореляційної залежності
Рис. 4.3 Приклад діаграми розсіювання за відсутності зв'язку між змінними
Оскільки ми маємо справу з випадковими величинами, однієї величини коефіцієнта парної кореляції для висновку недостатньо. Необхідно перевірити, чи значуще він відрізняється від нуля. Це можна зробити за допомогою критерію Стьюдента. Фактично перевіряється гіпотеза про рівність коефіцієнта кореляції нулю. Для цього розраховується критеріальне значення за формулою 4.3:
де r - значення коефіцієнта кореляції, N - кількість спостережень. Якщо розрахункове значення t (tроз) більше табличного, узятого з N - 2 ступенями, нульова гіпотеза відкидається. Це означає, що коефіцієнт кореляції значно відрізняється від нуля (з обраним рівнем значущості). Напівширина довірчого інтервалу для коефіцієнта кореляції визначається за формулою 4.4:
де N - кількість спостережень, за якими розраховується коефіцієнт кореляції; r - значення коефіцієнта кореляції; tn-2p - табличне значення критерію Стьюдента, узятого з N - 2 ступеня. Слід пам'ятати, що коефіцієнт кореляції показує міру тільки лінійного зв'язку. Тому у випадках, коли залежність між змінними має більш складний характер, коефіцієнт кореляції буде показувати відсутність зв'язку. Приклад - на рис. 4.4. між змінними існує залежність другого порядку (описується квадратним рівнянням), тоді як коефіцієнт кореляції буде близьким до нуля. Тому для виявлення складних залежностей між змінними використовують інші статистичні методи, зокрема, регресійний аналіз.
Рис. 4.4 Приклад нелінійного зв'язку між змінними Часткова кореляція Для того щоб вплив кореляційного зв'язку між двома змінними «очистити» від можливого впливу третьої, введене поняття часткової кореляції. За нею коефіцієнт кореляції між двома змінними X і Z визначається за формулою:
де r12, r13 і r23 - коефіцієнти парної кореляції між змінними X і Y, X і Z, Y і X відповідно. При використанні часткового коефіцієнта кореляції необхідно пам'ятати: · взаємовпливаючих змінних може бути не три, а скільки завгодно; · ви можете не знати про всі взаємовпливаючі змінні. Рангова кореляція є аналогом парної кореляції для тих випадків, коли величини, наявність зв'язку між якими потрібно перевірити, наведені не в шкалі відношень, а в який-небудь іншій. Найбільше часто така ситуація виникає, якщо ми маємо справу із суб'єктивними оцінками об'єктивних явищ, які не можна виміряти, тобто з експертними оцінками. Крім того, рангова кореляція використовується також у випадках, коли закон розподілу досліджуваних змінних не є гаусовським (нормальним). Коефіцієнти кореляції називаються ранговими, тому що перед обчисленням значення змінних перетворюють у ранги. Для цього наявні значення змінних розміщують у ранжированому (впорядкованому за величиною) ряді (значення у вихідному стані можуть бути таким проранжированим рядом). Потім кожному значенню присвоюється ранг від 1 до N, де N - кількість аналізованих об'єктів. У тому випадку якщо кілька елементів мають той самий ранг, то кожному з них присвоєються середнє від займаних ними місць. Допущення: · усі спостереження взаємно незалежні; · усі значення спостережень витягнуті з однієї і тієї двовимірної генеральної сукупності, тобто X і Y однаково розподілені. Існує кілька різних способів обчислення коефіцієнтів рангової кореляції. Найбільше часто використовують коефіцієнт кореляції Спірмена (r, іноді позначається rs) і коефіцієнт Кендалла (τ). Коефіцієнт кореляції Спірмена обчислюється за формулою 4.6:
де R1i і R2i - ранги i-го об'єкта для кожної з порівнюваних змінних. Значення r не залежить від способу упорядкування рангів. Очевидно, що цей коефіцієнт є повним аналогом коефіцієнта парної кореляції - після перетворення його можна записати у такому вигляді:
За наявності збіжних значень (зв'язків) знаменник зменшується на величину (формула 5.7):
де L1 і L2 - кількість зв'язків у T1i; T2J - розміри зв'язків (кількість елементів у них). Коефіцієнт кореляції Кендалла обчислюється за формулою 5.8:
де п - кількість спостережень; Q - число неузгоджених пар (ХjУj) і (Xi,Yi) для всіх комбінацій i і j. Пари називаються неузгодженими, якщо для них виконується така умова:
sign(Xj - Yj)sign(Xi - Yi) = -1, (4.10)
де sign - означає "знак". Ця функція набуває значення +1 для позитивного числа, а - 1 – для негативного. Іншими словами, наведена умова означає, що збільшення X приводить до зменшення Y і навпаки. Для перевірки значущості коефіцієнта існують спеціальні таблиці. Питання для самоконтролю 1.Дайте характеристику аналітичним методамдослідження 2. У чому особливість застосування методу формалізації? 3. Коли доцільно застосовувати математичне моделювання? 4. Яка мета застосування ймовірнісно-статистичних методів дослідження
|
||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 1699; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.011 с.) |

 (4.2)
(4.2)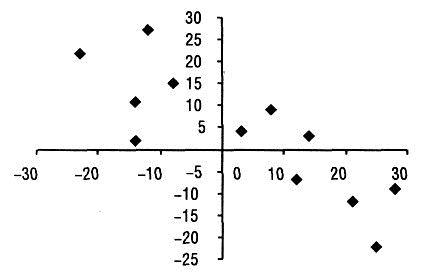


 , (4.3)
, (4.3) (4.4)
(4.4)
 (4.5)
(4.5)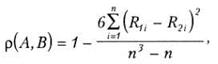 (4.6)
(4.6) (4.7)
(4.7) (4.8)
(4.8) (4.9)
(4.9)


