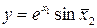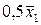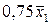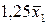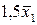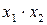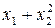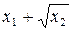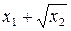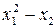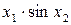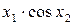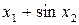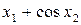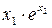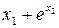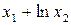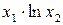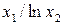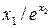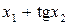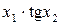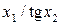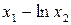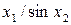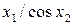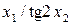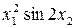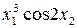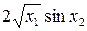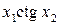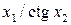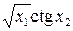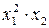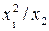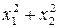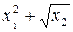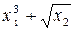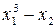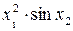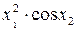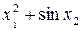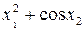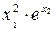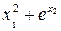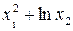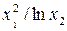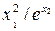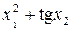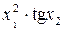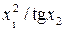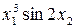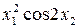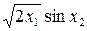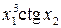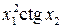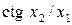Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розрахунково-графічна робота. Похибки прямих вимірюваньСодержание книги
Поиск на нашем сайте
Завдання У табл. 6.5 задані результати окремих вимірювань Приклад виконання завдання
Дані, за якими виконуються розрахунки, наведені в табл. 6.1, кінцеві результати розрахунків заносяться до табл. 6.2
Таблиця 6.1
Таблиця 6.2
Виконуємо обчислення і заносимо результати до табл. 6.3
Таблиця 6.3
Знаходимо середнє значення вимірюваної величини
Знаходимо стандартну похибку окремого вимірювання
Знаходимо критерій промаху для максимального значення
З табл. 1.2 для
Оскільки для Виконуємо обчислення для решти значень і заносимо результати до табл. 6.4
Таблиця 6.4
Знаходимо середнє значення вимірюваної величини
Знаходимо стандартну похибку окремого вимірювання
Знаходимо критерій промаху для максимального відхилення
З табл. 1.2 для Оскільки для значення З табл. 1.1 для Знаходимо випадкову похибку середнього значення вимірюваної величини
Знаходимо паспортну похибку приладу
Знаходимо похибку приладу, перераховану на надійну ймовірність
Гранична похибка середнього значення вимірюваної величини
Результат вимірювань із надійною ймовірністю
Відносна гранична похибка середнього значення вимірюваної величини
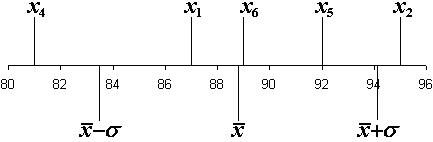
Будуємо діаграму розподілу похибок окремих вимірів (рис. 6.1).
Таблиця 6.5 Похибки прямих вимірювань
Продовження таблиці 6.5 Похибки прямих вимірювань
Продовження таблиці 6.5 Похибки прямих вимірювань
Розрахунково-графічна робота. Похибки непрямих вимірювань
Завдання
За заданими в табл. 7.4 результатами прямих вимірювань (середні значення
Номер Вашого варіанту відповідає двом останнім цифрам номера залікової книжки.
Приклад виконання завдання
Дані, за якими виконуються розрахунки, наведені в табл. 7.1, результати розрахунків заносяться до табл. 7.2
Таблиця 7.1
Таблиця 7.2
Знаходимо середнє значення результату непрямих вимірювань:
Оскільки гранична похибка
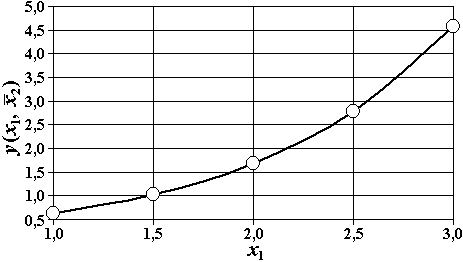
Значення коефіцієнтів Стьюдента Оскільки гранична похибка Знаходимо частинні похідні від функції
Знаходимо значення частинних похідних у точках середніх значень
Знаходимо граничну похибку результату непрямих вимірювань
Результат непрямих вимірювань подаємо у вигляді: Відносна гранична похибка середнього значення вимірюваної величини
Виконуємо необхідні розрахунки (див. табл. 7.3) і будуємо графік залежності
Таблиця 7.3
Таблиця 7.4 Похибки непрямих вимірювань
Продовження таблиці 7.4
Похибки непрямих вимірювань
Продовження таблиці 7.4 Похибки непрямих вимірювань
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 98; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.115.79 (0.013 с.) |

 , клас точності приладу
, клас точності приладу 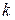 , мінімальне
, мінімальне 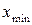 та максимальне
та максимальне 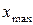 значення шкали приладу, потрібна надійна ймовірність
значення шкали приладу, потрібна надійна ймовірність  для 100 варіантів. Номер Вашого варіанту відповідає двом останнім цифрам номера залікової книжки. Перевірте ряд значень вашого варіанту на наявність промаху. Після вилучення промаху, якщо він є, знайдіть середнє значення
для 100 варіантів. Номер Вашого варіанту відповідає двом останнім цифрам номера залікової книжки. Перевірте ряд значень вашого варіанту на наявність промаху. Після вилучення промаху, якщо він є, знайдіть середнє значення  вимірюваної величини, стандартну похибку окремого вимірювання
вимірюваної величини, стандартну похибку окремого вимірювання  , випадкову похибку
, випадкову похибку 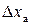 середнього значення вимірюваної величини, паспортну похибку приладу
середнього значення вимірюваної величини, паспортну похибку приладу  , похибку приладу
, похибку приладу 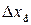 , граничну похибку
, граничну похибку  і відносну граничну похибку
і відносну граничну похибку 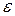 середнього значення вимірюваної величини. Побудуйте діаграму розподілу похибок окремих вимірів за зразком рис. 6.1.
середнього значення вимірюваної величини. Побудуйте діаграму розподілу похибок окремих вимірів за зразком рис. 6.1.





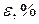


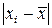

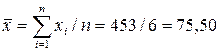 .
.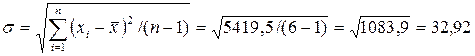 .
.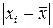
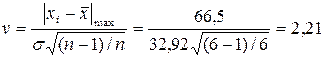 .
. ,
, 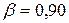 знаходимо максимальне припустиме значення критерію промаху
знаходимо максимальне припустиме значення критерію промаху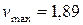 .
. , то значення
, то значення 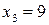 є промахом і підлягає вилученню.
є промахом і підлягає вилученню.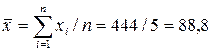 .
.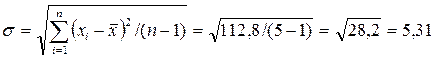 .
.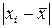
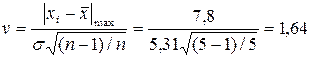 .
. ,
, 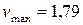 .
.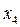 , що має максимальне відхилення
, що має максимальне відхилення 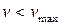 , то серія залишених результатів вимірювань не містить промахів.
, то серія залишених результатів вимірювань не містить промахів.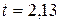 .
.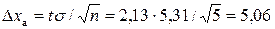 .
.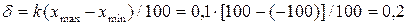 .
. .
.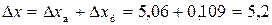 .
.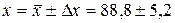 .
.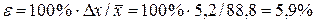 .
.
 , їхні граничні похибки
, їхні граничні похибки 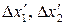 при надійних ймовірностях
при надійних ймовірностях 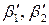 ) знайдіть середнє значення
) знайдіть середнє значення  результату непрямих вимірювань. Аргументи тригонометричних функцій даються в радіанах. Для заданого значення надійної ймовірності
результату непрямих вимірювань. Аргументи тригонометричних функцій даються в радіанах. Для заданого значення надійної ймовірності  ,
, 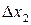 , граничну похибку
, граничну похибку 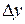 і відносну граничну похибку
і відносну граничну похибку 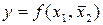 за зразком рис. 7.1.
за зразком рис. 7.1.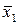
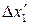
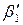
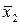

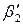
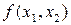

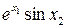
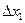
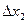
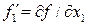
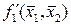
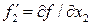
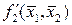
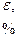

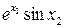
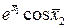
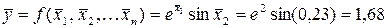 .
.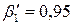 , а для результату
, а для результату  потрібна надійна ймовірність
потрібна надійна ймовірність 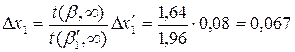 .
.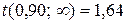 і
і 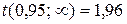 беремо з табл. 1.1.
беремо з табл. 1.1.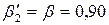 , то
, то 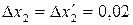 .
.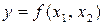 :
: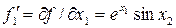 ;
; 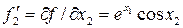 .
. :
: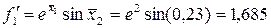 ;
;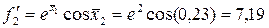 .
.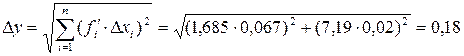 .
.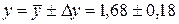 .
.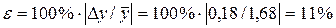 .
.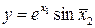 (рис. 7.1).
(рис. 7.1).