Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедри водопостачання, водовідведення,Содержание книги
Поиск на нашем сайте
Кафедри водопостачання, водовідведення, Раціонального використання і охорони водних ресурсів
МЕТОДИЧНІ ВКАЗІВКИ
ДО ВИКОНАННЯ РОЗРАХУНКОВО-ГРАФІЧНИХ РОБІТ З МЕТРОЛОГІЇ
(для студентів усіх спеціальностей)
ЗАТВЕРДЖЕНО На засіданні кафедри ВВ РВ і ОВР Протокол № 4 від 30.11.2012 р. На засіданні Ради Інституту міського будівництва та охорони навколишнього середовища Протокол № 4 від 18.12.2012 р.
м. Макіївка – 2013 р. УДК 53 (076. 5)
Методичні вказівки до виконання розрахунково-графічних робіт з метрології (для студентів усіх спеціальностей)./ В.І. Нездоймінов, Л.Г. Зайченко, В.С. Рожков, М.М. Голоденко.– м. Макіївка: ДонНАБА, 2013. – 63 с.
Посібник містить короткі методичні вказівки з опрацювання результатів експерименту. Викладені рекомендації спираються на основні закони теорії ймовірностей та математичної статистики. Докладно розглянута послідовність дій, що дозволяють осмислено і раціонально виконувати всі етапи опрацювання і подання експериментальних даних, а також оцінити похибки результатів вимірів. Конкретні приклади обробки результатів прямих і непрямих вимірів з використанням табличного процесора MS Excel або калькулятора допоможуть студентам засвоїти послідовність дій, здійснюваних при опрацюванні експериментальних даних. Даються також методичні рекомендації з наближених обчислень. Наводяться завдання розрахунково-графічних робіт із тем: «Похибки прямих вимірювань», «Похибки непрямих вимірювань», «Апроксимація методом найменших квадратів». Кожне з трьох завдань містить 100 індивідуальних варіантів, номери яких відповідають двом останнім цифрам номера залікової книжки студента. У тексті посібника містяться питання самоконтролю та відповіді на них із коментарями. Методичні вказівки призначені для студентів усіх спеціальностей, що вивчають курс метрології. Вони будуть також корисними для опрацювання результатів лабораторного експерименту при вивченні природничих та технічних дисциплін.
Рецензент: А.Я Найманов, д-р техн. наук, професор, (Донбаська національна академія будівництва і архітектури).
Відповідальний за випуск: Л.Г. Зайченко
1. ОСНОВИ ТЕОРІЇ ПОХИБОК
Типи похибок Розрізнюють три типи похибок вимірів. 1) Грубі помилки або промахи – похибки 2) Систематичні помилки викликаються факторами, що залишаються постійними (чи закономірно змінюються) при багаторазовому повторенні тих самих вимірів (тими ж приладами та однаковим методом). Вони у свою чергу поділяються на кілька груп. а) Поправки – помилки, величина і знак яких досить точно відомі, тому їх можна легко врахувати або усунути. Наприклад, при зважуванні тіла на терезах слід враховувати виштовхувальну силу повітря, що діє на нього. Систематична похибка виникає також при зсуві нуля шкали вимірювального приладу. Тому, перш ніж почати вимірювання манометром або іншим стрілочним приладом, слід упевнитися, що стрілка стоїть на нулі, і при необхідності підправити положення стрілки коректором. б) Приладові похибки – помилки відомого походження і відомої граничної величини, але невідомого знаку. Ці похибки обумовлені конструкцією приладу (тертям в осі стрілочного приладу, заокругленням, що його здійснюють цифрові або дискретні стрілочні прилади тощо). Приладова похибка за своєю природою є систематичною похибкою, але ані величина, ані знак її для даного конкретного приладу невідомі. Приладову похибку оцінюють у процесі випробувань великої серії однотипних приладів. Приладова (паспортна) похибка
де в) Методичні похибки можуть виникати через неможливість усунути або точно врахувати якісь фактори, що впливають на результат вимірювань. Так, наприклад, вимірюючи витрату за допомогою трикутного водозливу, ми користуємося емпіричною (заснованою на досліді і недостатньо обґрунтованою теоретично) формулою 3) Випадкові помилки спричиняються великою кількістю різних випадкових факторів, вплив яких на кожен окремий вимір різний і тому не може бути заздалегідь врахований. Це, наприклад, помилка паралаксу, яка виникає, коли око спостерігача розміщене не на перпендикулярі до шкали, що проходить через кінець стрілки приладу. Зрозуміло, що якщо дивитися на стрілку під різними кутами, то вона вказуватиме на різні поділки шкали. При зважуванні на терезах випадкові помилки спричиняються рухом повітря, тертям у підвісах терезів, вібрацією фундаменту будинку. Неконтрольованих факторів багато, вони мають різну природу і відрізняються інтенсивністю впливу на процес вимірювання. Треба вживати заходів задля усунення факторів, які дають найбільший внесок у випадкову помилку, але всі їх повністю усунути не вдасться. Так, для зменшення випадкових помилок при зважуванні аналітичні терези розміщують у корпусі, який захищає їх від рухів повітря, опора важеля виготовляється зі спеціальної сталі, агату або корунду, що зменшує тертя в підвісі, корпус терезів встановлюють на спеціальній підставці, яка амортизує коливання будинку. Випадкові похибки відхиляють результати окремих вимірів в обидва боки від істинного значення, і їхній вплив враховується математичним опрацюванням результатів серії вимірювань фізичної величини. Для оцінки випадкових похибок потрібне застосування методів математичної статистики, заснованої на законах теорії ймовірностей. Теорія похибок враховує лише випадкові похибки. У цій теорії, зокрема, доводиться, що якщо зробити ряд вимірів і знайти середнє арифметичне цього ряду, то випадкова помилка середнього значення буде меншою, ніж випадкова помилка результату окремого виміру. Таким чином, для зменшення впливу випадкових помилок на результат вимірювання, слід провести не одне, а декілька вимірювань. ПИТАННЯ САМОКОНТРОЛЮ 3. Систематичною чи випадковою є похибка у визначенні моментів часу за допомогою маятникового годинника, обумовлена зміною температури у приміщенні? Відповідь: СИСТЕМАТИЧНОЮ – дивись коментар 31, ВИПАДКОВОЮ – коментар 38.
ПИТАННЯ САМОКОНТРОЛЮ 4. У кінці пакувальної лінії цементного заводу продукція зважується на електронній вазі. Виявилося, що при проходженні повз цеха по залізничній колії потяга покази ваги дещо збільшуються або зменшуються. Яка похибка тут виникає: систематична чи випадкова? Відповідь: СИСТЕМАТИЧНА – дивись коментар 45, ВИПАДКОВА – коментар 52. Вилучення промахів
Критерій промаху
де Результат вимірювань є промахом і підлягає вилученню, якщо
Таблиця 1.2 Максимальне припустиме значення критерію промаху
Прямі виміри Непрямі виміри Інколи ми не можемо виміряти величину
Тест самоконтролю
Завдання У табл. 6.5 задані результати окремих вимірювань Приклад виконання завдання
Дані, за якими виконуються розрахунки, наведені в табл. 6.1, кінцеві результати розрахунків заносяться до табл. 6.2
Таблиця 6.1
Таблиця 6.2
Виконуємо обчислення і заносимо результати до табл. 6.3
Таблиця 6.3
Знаходимо середнє значення вимірюваної величини
Знаходимо стандартну похибку окремого вимірювання
Знаходимо критерій промаху для максимального значення
З табл. 1.2 для
Оскільки для Виконуємо обчислення для решти значень і заносимо результати до табл. 6.4
Таблиця 6.4
Знаходимо середнє значення вимірюваної величини
Знаходимо стандартну похибку окремого вимірювання
Знаходимо критерій промаху для максимального відхилення
З табл. 1.2 для Оскільки для значення З табл. 1.1 для Знаходимо випадкову похибку середнього значення вимірюваної величини
Знаходимо паспортну похибку приладу
Знаходимо похибку приладу, перераховану на надійну ймовірність
Гранична похибка середнього значення вимірюваної величини
Результат вимірювань із надійною ймовірністю
Відносна гранична похибка середнього значення вимірюваної величини
Будуємо діаграму розподілу похибок окремих вимірів (рис. 6.1).
Таблиця 6.5 Похибки прямих вимірювань
Продовження таблиці 6.5 Похибки прямих вимірювань
Продовження таблиці 6.5 Похибки прямих вимірювань
|
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 106; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.175.166 (0.009 с.) |

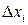 , які істотно перевищують очікувані в умовах даного експерименту значення (у три і більше разів). Промах може бути спричинений використанням несправних приладів, неуважністю або неакуратністю експериментатора (недодержання правил роботи з приладом, неправильний відлік показів, помилки в записі результатів тощо). Виявивши промах, результат вимірювання слід відкинути. Виявленню промахів сприяє порівняння результатів вимірювань, отриманих різними експериментаторами.
, які істотно перевищують очікувані в умовах даного експерименту значення (у три і більше разів). Промах може бути спричинений використанням несправних приладів, неуважністю або неакуратністю експериментатора (недодержання правил роботи з приладом, неправильний відлік показів, помилки в записі результатів тощо). Виявивши промах, результат вимірювання слід відкинути. Виявленню промахів сприяє порівняння результатів вимірювань, отриманих різними експериментаторами. звичайно вказується в паспорті приладу. Вимірювальні прилади поділяються на вісім класів точності: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0. Число, що визначає клас точності, вказується на шкалі приладу. Воно являє собою приладову похибку, виражену у відсотках від діапазону значень шкали:
звичайно вказується в паспорті приладу. Вимірювальні прилади поділяються на вісім класів точності: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0. Число, що визначає клас точності, вказується на шкалі приладу. Воно являє собою приладову похибку, виражену у відсотках від діапазону значень шкали: ,
,
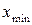 і
і 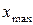 – мінімальне та максимальне значення шкали приладу. Найчастіше
– мінімальне та максимальне значення шкали приладу. Найчастіше  . Але в вакуум-манометрах, наприклад, мінімальне значення шкали може бути від’ємним:
. Але в вакуум-манометрах, наприклад, мінімальне значення шкали може бути від’ємним: 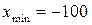 ,
, 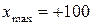 . У частотомірах, що використовуються для вимірювань у міській електромережі, може бути
. У частотомірах, що використовуються для вимірювань у міській електромережі, може бути  ,
, 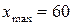 . Якщо клас точності приладу не вказаний, то
. Якщо клас точності приладу не вказаний, то 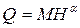 . До речі, більшість формул гідравліки є емпіричними, а отже вносять методичні похибки. У багатьох випадках методичні похибки виникають внаслідок використання наближених формул, що не враховують швидкісного напору. Методичні похибки можуть бути обумовлені також впливом на предмет виміру самого приладу (наприклад, термометр, занурений у посудину з невеликою кількістю рідини, змінює її температуру). Ще однією причиною методичних помилок може бути невизначеність параметрів самого вимірюваного об’єкта (наприклад, при вимірюванні діаметра труби, переріз якої ми вважаємо коловим і який насправді є еліптичним з невеликим ексцентриситетом, непомітним для ока). До методичних можна також віднести помилки при заокругленні чисельних значень величин, при використанні наближених методів обчислень, які не забезпечують необхідну точність.
. До речі, більшість формул гідравліки є емпіричними, а отже вносять методичні похибки. У багатьох випадках методичні похибки виникають внаслідок використання наближених формул, що не враховують швидкісного напору. Методичні похибки можуть бути обумовлені також впливом на предмет виміру самого приладу (наприклад, термометр, занурений у посудину з невеликою кількістю рідини, змінює її температуру). Ще однією причиною методичних помилок може бути невизначеність параметрів самого вимірюваного об’єкта (наприклад, при вимірюванні діаметра труби, переріз якої ми вважаємо коловим і який насправді є еліптичним з невеликим ексцентриситетом, непомітним для ока). До методичних можна також віднести помилки при заокругленні чисельних значень величин, при використанні наближених методів обчислень, які не забезпечують необхідну точність. ,
,
 - максимальне в серії окремих вимірювань відхилення результату від середнього значення.
- максимальне в серії окремих вимірювань відхилення результату від середнього значення. , де
, де  - максимальне можливе значення критерію промаху
- максимальне можливе значення критерію промаху  , яке виникає внаслідок статистичного розкиду при заданій надійній імовірності
, яке виникає внаслідок статистичного розкиду при заданій надійній імовірності  . Значення
. Значення 




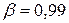
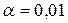
 безпосередньо, але знаємо, що її можна розрахувати за формулою
безпосередньо, але знаємо, що її можна розрахувати за формулою  , де
, де  - величини, які виміряти безпосередньо можна. Умови експерименту з вимірювання величин
- величини, які виміряти безпосередньо можна. Умови експерименту з вимірювання величин  . Вказаний довірчий інтервал відповідає надійній імовірності
. Вказаний довірчий інтервал відповідає надійній імовірності
 , клас точності приладу
, клас точності приладу 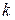 , мінімальне
, мінімальне  вимірюваної величини, стандартну похибку окремого вимірювання
вимірюваної величини, стандартну похибку окремого вимірювання  , випадкову похибку
, випадкову похибку 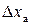 середнього значення вимірюваної величини, паспортну похибку приладу
середнього значення вимірюваної величини, паспортну похибку приладу 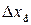 , граничну похибку
, граничну похибку  і відносну граничну похибку
і відносну граничну похибку 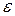 середнього значення вимірюваної величини. Побудуйте діаграму розподілу похибок окремих вимірів за зразком рис. 6.1.
середнього значення вимірюваної величини. Побудуйте діаграму розподілу похибок окремих вимірів за зразком рис. 6.1.





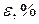


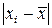

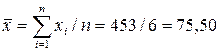 .
.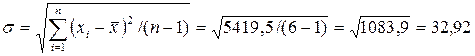 .
.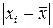
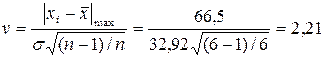 .
. ,
, 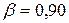 знаходимо максимальне припустиме значення критерію промаху
знаходимо максимальне припустиме значення критерію промаху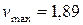 .
.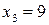 є промахом і підлягає вилученню.
є промахом і підлягає вилученню.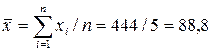 .
.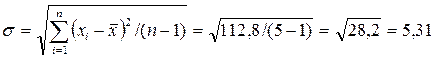 .
.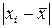
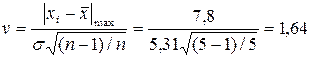 .
. ,
, 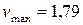 .
.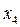 , що має максимальне відхилення
, що має максимальне відхилення 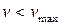 , то серія залишених результатів вимірювань не містить промахів.
, то серія залишених результатів вимірювань не містить промахів.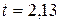 .
.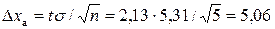 .
.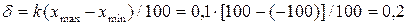 .
. .
.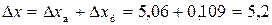 .
.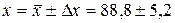 .
.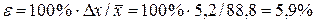 .
.