
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розрахунки з використанням калькулятораСодержание книги
Поиск на нашем сайте
Якщо Ви не маєте можливості скористатися табличним процесором MS Excel, доведеться виконувати розрахунки на калькуляторі. Для впорядкування розрахунків будуємо таблицю (див. табл. 2.1). Таблиця 2.1 Знаходження
Знаходимо середнє значення вимірюваної величини
Знаходимо стандартне відхилення
Для максимального відхилення результату окремого виміру від середнього
З табл. 1.2 при рівні значущості Таблиця 2.2 Знаходження
Знаходимо середнє значення вимірюваної величини
Знаходимо стандартне відхилення
Знаходимо стандартну похибку середнього
Знаходимо випадкову похибку
З табл. 1.1 при рівні значущості Для максимального відхилення результату окремого виміру від середнього
З табл. 1.2 при рівні значущості Похибка приладу, перерахована на надійну ймовірність
Границя довірчого інтервалу
Відносна похибка
Результат вимірювань подаємо у вигляді
Непрямі виміри Інколи ми не можемо виміряти величину
Відтворювані умови експерименту
Для кожного результату прямих вимірів Середнє значення результату непрямих вимірювань
де Якщо гранична похибка
де Гранична похибка результату непрямих вимірювань
де
Таблиця 2.3 Похідні деяких функцій
Дуже часто функція
Результат непрямих вимірювань подаємо у вигляді:
із зазначенням одиниці вимірювання і надійної ймовірності. Відносна гранична похибка середнього значення вимірюваної величини
Невідтворювані умови експерименту
У кожному з
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 111; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.94.112 (0.009 с.) |

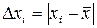 і
і 



 .
.
 .
.
 критерій промаху
критерій промаху .
.
 і числі вимірів
і числі вимірів  максимальне допустиме значення критерію промаху
максимальне допустиме значення критерію промаху  . Оскільки
. Оскільки 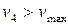 , то результат виміру
, то результат виміру  є промахом і підлягає вилученню. Будуємо табл. 2.2 за зразком табл. 2.1, вилучивши елемент
є промахом і підлягає вилученню. Будуємо табл. 2.2 за зразком табл. 2.1, вилучивши елемент  .
.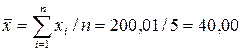 .
.
 .
.
 .
.
 .
.
 коефіцієнт Стьюдента
коефіцієнт Стьюдента  .
.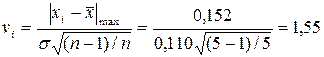 .
.
 . Оскільки найбільше значення критерію промаху не перевищує максимального допустимого
. Оскільки найбільше значення критерію промаху не перевищує максимального допустимого  , то вибіркова сукупність не містить промахів.
, то вибіркова сукупність не містить промахів. ,
, .
.
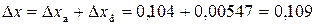 .
.
 .
.
 із зазначенням одиниці вимірювання і надійної ймовірності:
із зазначенням одиниці вимірювання і надійної ймовірності: 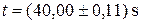 при
при  .
. безпосередньо, але знаємо, що її можна розрахувати за формулою
безпосередньо, але знаємо, що її можна розрахувати за формулою  , де
, де  - величини, які виміряти безпосередньо можна. Умови експерименту з вимірювання величин
- величини, які виміряти безпосередньо можна. Умови експерименту з вимірювання величин  раз вимірюємо кожну з величин
раз вимірюємо кожну з величин  і граничну похибку
і граничну похибку 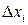 .
. ,
,
 – середні значення величин
– середні значення величин  , виміряних безпосередньо.
, виміряних безпосередньо.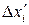 середнього значення деякої величини
середнього значення деякої величини  , а для
, а для 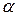 , то перераховуємо граничну похибку до заданої надійної ймовірності за формулою
, то перераховуємо граничну похибку до заданої надійної ймовірності за формулою ,
,
 – коефіцієнт Стьюдента [MS Excel СТЬЮДРАСПОБР(
– коефіцієнт Стьюдента [MS Excel СТЬЮДРАСПОБР(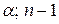 )] для рівня значущості
)] для рівня значущості  – коефіцієнт Стьюдента для рівня значущості
– коефіцієнт Стьюдента для рівня значущості 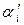 і нескінченної кількості вимірювань.
і нескінченної кількості вимірювань. ,
,
 – частинні похідні від функції
– частинні похідні від функції  , взяті в точках середніх значень
, взяті в точках середніх значень 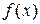




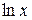
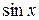






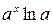




 має вигляд
має вигляд  , де
, де  - показники степеня, які можуть бути як додатними, так і від’ємними. Можна показати, що в цьому випадку формула (31) набуває вигляду:
- показники степеня, які можуть бути як додатними, так і від’ємними. Можна показати, що в цьому випадку формула (31) набуває вигляду: .
.
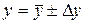
 .
.
 . Далі знаходимо середнє арифметичне значення
. Далі знаходимо середнє арифметичне значення  . Межі довірчого інтервалу оцінюються так само, як і для прямих вимірів, тобто за формулами (8) і (9).
. Межі довірчого інтервалу оцінюються так само, як і для прямих вимірів, тобто за формулами (8) і (9).


