
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розрахунково-графічна робота. Лінійна апроксимаціяСодержание книги
Поиск на нашем сайте
Номер Вашого варіанту відповідає двом останнім цифрам номера залікової книжки.
Завдання А для варіантів 01 – 25
Відомо, що між величинами
Приклад виконання завдання А Дані, за якими виконуються розрахунки, наведені в табл. 8.1, кінцеві результати розрахунків заносяться до табл. 8.2 Таблиця 8.1
Таблиця 8.2
Виконуємо обчислення і заносимо результати до табл. 8.3
Таблиця 8.3
З табл. 1.1 знаходимо коефіцієнт Стьюдента Знаходимо випадкову похибку середнього значення вимірюваної величини
Результат вимірювань із надійною ймовірністю
Відносна гранична похибка середнього значення вимірюваної величини
Відкладаємо на графіку рис. 8.1 експериментальні точки і будуємо пряму
Таблиця 8.4 Лінійна апроксимація.Завдання А
Завдання B для варіантів 26 – 50 Відомо, що між величинами Приклад виконання завдання В
Дані, за якими виконуються розрахунки, наведені в табл. 8.5, кінцеві результати розрахунків заносяться до табл. 8.6 Таблиця 8.5
Таблиця 8.6
Виконуємо обчислення і заносимо результати до табл. 8.7.
Таблиця 8.7
З табл. 1.1 знаходимо коефіцієнт Стьюдента Знаходимо випадкові похибки середніх значень вимірюваних величин
Результат вимірювань із надійною ймовірністю
Відносні граничні похибки середніх значень вимірюваних величин
Відкладаємо на графіку рис. 8.2 експериментальні точки і будуємо пряму
Таблиця 8.8 Лінійна апроксимація.Завдання В
Завдання С для варіантів 51 - 75 Втрати напору по довжині труби Приклад виконання завдання С Дані, за якими виконуються розрахунки, наведені в табл. 8.9, кінцеві результати розрахунків заносяться до табл. 8.10 Таблиця 8.9
Таблиця 8.10
Втрати напору по довжині труби Виконуємо обчислення і заносимо результати до табл. 8.11
Таблиця 8.11
З табл. 1.1 знаходимо коефіцієнт Стьюдента Знаходимо випадкову похибку середнього значення величини
Оскільки
Відносна гранична похибка середнього значення прискорення
Відкладаємо на графіку рис. 8.3 експериментальні точки
Таблиця 8.12 Лінійна апроксимація.Завдання С
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 205; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.008 с.) |

 і
і  , наведеними в табл. 8.4, існує лінійна залежність
, наведеними в табл. 8.4, існує лінійна залежність  . Знайдіть середнє значення
. Знайдіть середнє значення 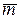 коефіцієнта
коефіцієнта  , випадкову похибку
, випадкову похибку  і відносну граничну похибку
і відносну граничну похибку  середнього значення коефіцієнта
середнього значення коефіцієнта  . Побудуйте графік лінійної залежності
. Побудуйте графік лінійної залежності  і нанесіть на графік експериментальні точки.
і нанесіть на графік експериментальні точки.

















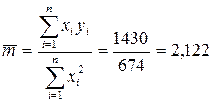 ;
;  .
. .
.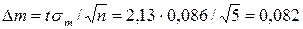 .
. подаємо у вигляді:
подаємо у вигляді: .
. .
. . Підставляємо в рівняння прямої
. Підставляємо в рівняння прямої 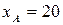 . Отримуємо
. Отримуємо  . Проводимо пряму через точки
. Проводимо пряму через точки  і
і  .
.
 .
.
 . Знайдіть середні значення
. Знайдіть середні значення  коефіцієнтів
коефіцієнтів  , випадкові похибки
, випадкові похибки  , а також відносні граничні похибки
, а також відносні граничні похибки  середніх значень коефіцієнтів
середніх значень коефіцієнтів  і нанесіть на графік експериментальні точки.
і нанесіть на графік експериментальні точки.





 ;
; 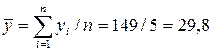 ;
; ;
; ;
; ;
;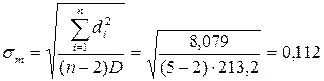 ;
;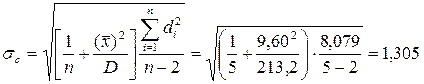 .
. ;
; .
. ;
;  .
.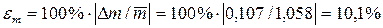 ;
; .
. . Підставляємо в рівняння прямої
. Підставляємо в рівняння прямої  і
і  . Отримуємо
. Отримуємо  ;
; 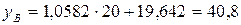 . Проводимо пряму через точки
. Проводимо пряму через точки  і
і  .
.
 .
.
 . Для труби довжиною l = 100 m вимірюється витрата
. Для труби довжиною l = 100 m вимірюється витрата 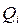 при напорі
при напорі  . Треба знайти питомий опір труби
. Треба знайти питомий опір труби 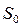 , а також оцінити похибку отриманого значення. У табл. 8.12 наведені результати окремих вимірювань – пари значень
, а також оцінити похибку отриманого значення. У табл. 8.12 наведені результати окремих вимірювань – пари значень  у вигляді лінійної залежності
у вигляді лінійної залежності 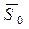 питомого опору труби, похибку
питомого опору труби, похибку  і відносну граничну похибку
і відносну граничну похибку  середнього значення
середнього значення 
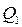




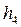




 .
.



 ;
; .
. .
.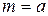 , то результат вимірювань із надійною ймовірністю
, то результат вимірювань із надійною ймовірністю 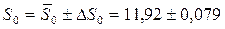 .
.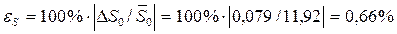 .
.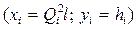 і будуємо пряму
і будуємо пряму  . Підставляємо в рівняння прямої
. Підставляємо в рівняння прямої  . Отримуємо
. Отримуємо  . Проводимо пряму через точки
. Проводимо пряму через точки  і
і 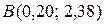 .
.



