
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Похибки посередніх вимірюваньСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Р. Є. БУБЛЕЙ, Є. М. БУБЛЕЙ
Фізичний ПРАКТИКУМ ДЛЯ ПІДГОТОВЧИХ ВІДДІЛЕНЬ
Допущено Міністерством вищої і середньої спеціальної освіти УРСР як навчальний посібник для слухачів підготовчих відділень вузів
ВИДАВНИЧЕ ОБ’ЄДНАННЯ «ВИЩА ШКОЛА>> ГОЛОВНЕ ВИДАВНИЦТВО КИЇВ — 1974 Б90
УДК 53 (076.5)-
Физический практикум. Для подготовительных отделений. Б у б л е й Р. E., Б у б л е й E. Н. Издательское объединение «Вища школа», 1974, 112 с. (на украинском языке). Цель пособия — на небольшом количестве лабораторных работ (20) закрепить основные идеи и законы физики, которые изучались в школе. Практикум написан с учетом новых программ. Все величины даны в Международной системе единиц (СИ). Работы описаны достаточно подробно, поэтому их можно выполнять как после повторения всего курса, так и после изучения отдельных тем. Большое внимание уделено изложению основ теории ошибок, иллюстрации ее применений. Пособие предназначено для слушателей подготовительных отделений вузов. Его можно также использовать для проведения лабораторных работ в средних школах и техникумах. Табл. 18. Ил. 56. Библиогр. 4.
Редакція літератури з математики і фізики Зав. редакцією А. С. Макуха
Видавниче об’єднання «Вища школа», 1974. Передмова
Викладання фізики на підготовчих відділеннях вузів має своїм завданням не тільки повторення загальнообов’язкової програми середньої школи, а й створення фундаменту для осмисленого і глибокого засвоєння слухачами загальноосвітніх і спеціальних дисциплін вузу. При стислих строках повторення курсу фізики доцільно приділити більше уваги теорії і лекційним демонстраціям, а практикум провести в кінці курсу на невеликій кількості добре продуманих лабораторних робіт, що містять відомості з різних розділів. Така форма проведення практикуму, як показує досвід, дає змогу слухачам виконати лабораторні роботи на високому рівні, ще раз і більш ефективно повторити й засвоїти теоретичний курс. Важливим елементом практикуму є виховання вдумливого ставлення до виконання і результатів експерименту. Тому автори вважали за доцільне ввести в посібник основи теорії похибок. Положення теорії проілюстровано прикладами. Проведенню лабораторних робіт повинно передувати вступне заняття, на якому слухачів ознайомлюють з правилами поведінки в лабораторії, технікою вимірювань, обробкою результатів і обчисленням похибок. Кожна лабораторна робота розрахована на дві години. Щоб забезпечити самоконтроль підготовленості до виконання роботи, до кожного завдання розроблено контрольні запитання. Для кращої підготовки до виконання лабораторних робіт у кінці кожної з них наведено два варіанти потрібної літератури. Посібник підготовлено як підсумовуючий практикум для виконання після вивчення всього теоретичного курсу. Досить докладний опис робіт дає можливість використати його на підготовчих відділеннях вузів, у середніх школах і технікумах для проведення лабораторних робіт "протягом навчального року. Автори висловлюють подяку В. Г. Чепуренку, 3. П. Двоскіну і А. І. Бублей за перегляд рукопису і конкретні поради. Зауваження щодо поліпшення якості посібника надсилати на адресу: 252054, Київ, 54, Гоголівська, 7, Головне видавництво видавничого об’єднання «Вища школа», редакція літератури з математики і фізики. Автори Розділ І ВИМІРЮВАННЯ І ОБРОБКА ЇХ РЕЗУЛЬТАТІВ Фізика стала наукою з того часу, коли її основним методом пізнання став експеримент. При його виконанні проводяться вимірювання, тобто визначення, у скільки разів вимірювана величина більша чи менша за величину, узяту за одиницю. Ніяке вимірювання не можна виконати абсолютно точно. Тому результатом будь-якого вимірювання є наближене число, величина якого тим ближча до справжнього значення, чим менша похибка. Знаходження похибки вимірювання дає змогу встановити границі існування шуканої величини. Наприклад, вимірюванням установлено, що “довжина тіла l= 0,453 м, а похибка становить ±0,001 м. Це означає, що шукана величина обмежена границями 0,452 м < / < 0,454 м. Таким чином, зазначення похибки вимірювання значною мірою компенсує неможливість установлення точного значення величини. Виміряти яку-небудь величину — це означає визначити результат вимірювання й похибку, допущену при його знаходженні. Вимірювання можуть бути безпосередніми і посередніми. § 1. ПОХИБКИ БЕЗПОСЕРЕДНІХ ВИМІРЮВАНЬ При безпосередньому вимірюванні числове значення величини знаходять внаслідок безпосереднього порівняння її з одиницею вимірювання за допомогою приладів. Так, наприклад, довжину вимірюють за допомогою метра, тиск — за допомогою манометра і т. п. Похибки при вимірюваннях бувають систематичні і випадкові. Систематичні похибки виникають від користування несправними або неправильно встановленими приладами, внаслідок недосконалості методів вимірювань і обчислена. Характерною особливістю таких похибок є їх обов’язкова повторюваність при кожному вимірюванні. Так, систематично повторюватиметься похибка при вимірюванні довжини урізаним метром, при вимірюванні сили струму амперметра з викривленою стрілкою, температури — за зміщеною шкaлою термометра та ін. Систематичні похибки можна виявити і врахувати. Випадкові похибки виникають незалежно від дослідника з різних причин. Наприклад, під час вимірювань може непомітно зміститись око спостерігача або повітряна течії може змістити стрілку приладу. Передбачити й усунути тaкі похибки неможливо. Треба навчитися знаходити їх i враховувати. Ознайомимося з властивостями і методами знаходження випадкових похибок. Позначимо результати п окремих ви- мірювань шуканої величини А через а1 , а2,…. ап. Характерною особливістю випадкових похибок є те, що при багаторазових вимірюваннях похибки однакової величини н бік збільшень або зменшень зустрічаються однаково часто. Тому загальна алгебраїчна сума випадкових похибок при багаторазових вимірюваннях величини А дорівнюватиме нулю, а середнє арифметичне значення а результатів n вимірювань
при великому n буде близьке до істинного значення А. Це середнє значення а і беруть за результат вимірювання. Різницю між середнім значенням величини і результатом окремого вимірювання називатимемо похибкою цього вимірювання. Так, похибка першого вимірювання ∆ах = а — — а1, похибка другого ∆ а2 — а — а2, похибка n-го 1 вимірювання ∆ аn = а — ап. Середнє арифметичне з n абсолютних значень виявлених похибок дає середню похибку, або похибку результату:
____________ Вираз ∆ аn = а — аn точніше слід було б називати практично визначуваною похибкою, на відміну від істинної похибки ∆ аn = А — аn, яка нам невідома, бо невідоме істинне значення А. Пам’ятаючи де, залишимо все ж за ∆ аn назву похибки для зручності. ____________ Виміряти яку-небудь величину А — це означає знайти її середнє значення а і середню похибку ∆ а. Тому
Написання двох знаків (±) перед середньою похибкою показує, що шукана величина обмежена границями (а + ∆ а) > А > (а — ∆а). Для порівняння точності різних вимірювань ще не досить визначити похибку. Справді, якщо результат вимірювання довжини одного тіла 0,010 ± 0,005 м, а другого — 1,000 ± 0,005 м, то хоч похибки в обох випадках і однакові, проте друге тіло виміряне значно точніше (0,005 м від їм становить усього 0,5%, а 0,005 м від0,01м — 50%). Для порівняння точності вимірювань користуються поняттям відносної похибки. Відносною похибкою є називають відношення середньої похибки ∆ аn до середнього значення величини а:
Звичайно відносну похибку визначають у процентах. У розглянутому вище прикладі порівняння точності вимірювань 0,010 м і 1 м відносна похибка буде відповідно:
Порівняння відносних похибок виразно показує, що 1 м виміряно з точністю в 100 раз більшою, ніж 0,01 м. Похибки числових значень величин, узятих з довідкових таблиць, при відсутності достатніх даних беруть такими, що дорівнюють половині одиниці останнього розряду, а при наявності даних розраховують. Приклад. Визначити похибку і відносну похибку числа Беручи значення =0,002 і відносну похибку Інколи при вимірюваннях допускають промахи — похибки великої величини, що спотворюють результати. Вони виникають внаслідок недбалості, недосвідченості або втоми експериментатора. їх відкидають як помилкові. III.Висновки Результат експерименту показує, що числове значення прискорення вільного падіння на місці досліду повинно задовольняти нерівність: 9,7 <g<10,l м/с2. Так експериментально встановлюють верхню і нижню границі прискорення вільного падіння g. Правильність такого висновку підтверджується тим, що вірне значення g (взяте з довідника для певної місцевості) дійсно вкладається в ці границі. Примітка. Наведена схема обробки результатів вимірювань з однією запасною цифрою (l) корисна для початківців, проте не завжди виправдана. У багатьох випадках результат можна дістати швидше, якщо перед початком роботи проаналізувати розрахункову формулу для сумарної похибки з точки зору похибок, які дають наявні прилади і методи вимірювання. Так, у розглянутому прикладі з формули похибок (2) випливає, що при визначенні g велику похибку дає вимірювання Т (похибка Т подвоюється). В учбових лабораторіях при знаходженні g маятником звичайний секундомір дає можливість визначити період коливання з точністю до трьох значущих цифр. Тому четверту значущу цифру як запасну при вимірюваннях і розрахунках З результатів вимірювань
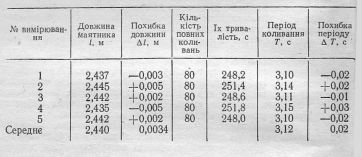
При визначенні На закінчення наведемо зразок оформлення звіту про виконану роботу. Його теоретичну частину з малюнками, схемами і розграфленою таблицею для заповнення результатами досліду підготовляють дома. На лабораторному занятті виконують вимірювання, обчислюють результати, їх похибки. Зразок ЛАБОРАТОРНА РОБОТА № 4 Визначення прискорення вільного падіння за допомогою маятника. Математичним маятником називають коливну систему що складається з матеріальної точки, підвішеної на тонкій і нерозтяжній нитці. Період коливань Т маятника, його довжина
яку можна застосовувати лише при малих кутах відхилення (2—4°). Довжину маятника виміряно лінійкою, період коливання вираховано як частку від ділення часу декількох десятків коливань (вимірювали секундоміром) на їх число. Результати вимірювання наведено в таблиці:
§ 4. ОСНОВНІ ПРИЛАДИ ДЛЯ ПІДВИЩЕННЯ ТОЧНОСТІ ВИМІРЮВАНЬ Ноніус. Операція безпосереднього вимірювання зводиться до порівняння вимірюваної величини з масштабом. Так, вимірюючи довжину тіла АВ (рис. 1, а), прикладають його до масштабної лінійки і порівнюють безпосередньо, у скільки разів довжина тіла більша за довжину найменшої поділки масштабу (відлічують поділки проти кінців А і .В). При цьому кількість десятих частин поділки оцінюють на око. Якщо довжину поділки взято за одиницю, то таке порівняння дасть кількість одиниць довжини і їх часток у тілі. Точність відліку по шкалі обмежується ціною її поділки, тобто значенням найменшої поділки. Око може впевнено відрізняти, в якій з половин поділки міститься край вимірюваного предмета. Тому вважають, що точність вимірювання становить не більше половини ціни найменшої поділки шкали. Точність до десятої частини поділки може дати лише добре треноване око, але й воно краще впорається з цим за допомогою ноніуса або мікрометричного гвинта. Ноніусом називають допоміжну лінійку, яку застосовують разом з масштабною для відлічування десятих, двадцятих або п’ятдесятих-часток міліметра. Якщо ноніус призначено для вимірювання десятих часток міліметра, то на ньому відстань 19 або 9 мм поділено на 10 рівних частин. Тут довжина кожної поділки ноніуса становить 1,9 або 0,9 мм, отже, розбіжність між однією поділкою лінійки і однією поділкою ноніуса становить 0,1 мм. Це число називають точністю ноніуса. Якщо приставити таку ноніусну лінійку до тіла, довжина якого більша за 14 мм і менша за 15 мм (рис. 1, б), то коли шоста поділка ноніуса збігається з будь-якою поділкою масштабної лінійки, різниця між кінцем В тіла і чотирнадцятою поділкою масштабної лінійки становитиме 0,6 мм, тобто загальна довжина тіла буде 14,6 мм. Оскільки точність вимірювання визначається точністю ноніуса, то в цьому випадку вона буде 0,1 мм. У загальному випадку, якби в ноніусі п — 1 поділок масштабної лінійки були поділені на п частин, то при довжині тіла АВ, що становить т цілих поділок масштабу і при збігу ℜ-ї поділки ноніуса з будь-якою поділкою масштабної лінійки довжина тіла дорівнювала б AB = Практичне застосування ноніус має в штангенциркулі для вимірювання довжини, у коловому ноніусі — для вимірювання градусів дуги тощо. Мікрометричний гвинт. Мікрометричний гвинт є основною частиною ряду приладів, наприклад мікрометра, приладу для вимірювання товщини з точністю до 0,01; 0,02; 0,04 мм. Мікрометр (рис. 2) складається з масивної скоби А з полірованою п’яткою В на одному кінці, а через другий кінець М проходить мікрометричний гвинт СБ з кроком різі 0,5 мм. До останнього прикріплено барабан Б, який по ободу НК поділений на 50 поділок. На поверхні гвинтової муфти М зроблено міліметрові поділки так, що коли край барабана (НК) збігається з 0 шкали //, кінець С мікрометричного гвинта доторкається до п’ятки.
Якщо хід гвинта становить 0,5 мм, а обід барабана має 50 поділок, то при повертанні барабана на одну поділку відстань ВС змінюється на 0,01 мм, при повертанні на дві поділки — на 0,02 мм і т. д. Отже, відстань ВС завжди дорівнює такому числу міліметрових і пів міліметрових поділок, скільки поділок масштабної лінійки // повністю вийшло з-під барабана, плюс стільки сотих частин міліметра, скільки показує номер поділки барабана, яка збігається з лінією //. Щоб мікрометричний гвинт завжди точно однаково тиснув на вимірюване тіло, яке міститься між точками В і С, до барабана Б прикріплено спеціальну запобіжну головку або тріскачку Т. Підводячи мікрометричний гвинт близько до п’ятки або вимірюваного тіла, обертати барабан пальцями перестають і продовжують його обертати за допомогою тріскачки. __________________________________________________________ РозділІІ ЛАБОРАТОРНІ РОБОТИ Робота І ПЕРЕВІРКА ЗАКОНІВ ПРЯМОЛІНІЙНОГО РУХУ НА ПРИЛАДІ АТВУДА Устаткування: прилад Атвуда з набором важків, секундомір. Теоретичний вступ
Якщо на систему діяти сталою силою і безперервно, наприклад вагою додаткового важка Ра, то система важків, набуваючи сталого прискорення, рухатиметься рівно прискорено. Величина цього прискорення а визначається другим законом динаміки: прискорення, якого набуває тіло під дією сили F дорівнює відношенню цієї сили до маси тіла m, тобто а = У цьому випадку діюча сила дорівнює вазі додаткового важка Ра = mag, маса рухомої системи дорівнює сумі мас обох важків 2m і додаткового важка ma. Тому
При такому рівноприскореному русі без початкової швидкості шлях з повинен змінюватись пропорційно квадрату часу руху t S= а швидкість v — пропорційно його першому степеню v=at (3) Звідси випливає, що шлях s1 за першу секунду руху чисельно дорівнює половині прискорення s1= a=v1=2s1 (4) Це дає нам основу дослідної перевірки прискорення а, знайденого за законами динаміки: прискорення а чисельно повинно бути вдвічі більшим за шлях пройдений за першу секунду, і повинно чисельно дорівнювати швидкості v1, набутій в кінці першої секунди. Величину s1 можна виміряти на досліді безпосередньо. Що ж до швидкості v1 в кінці першої секунди, то слід пригадати, що вона дорівнює тій швидкості рівномірного руху, яку мало б тіло, якби, починаючи з кінця першої секунди, воно рухалося рівномірно. Швидкість рівномірного руху чисельно дорівнює шляху, пройденому за секунду. Виходячи з викладеного, перевірити закони динаміки і кінематики можна так. 1)Протягом першої секунди систему примушують рухатись рівно прискорено під дією сталої сили ваги важка Ра. 2) Довжину шляху s1, пройденого за цей час, вимірюють безпосередньо, спостерігаючи з секундоміром за рухом важків уздовж шкали. 3)В кінці першої секунди затримують прискорюючий важок Ра, надаючи системі можливість рухатись без прискорення з швидкістю, набутою системою до цього часу. 4)Продовжуючи спостерігати за рухом важків уздовж шкали, вимірюють відстань, пройдену за другу секунду при рівномірному русі. Вона чисельно дорівнює швидкості v 1. 5)Порівнюють прискорення, знайдені за результатами п. 2 і п. 4 на основі (4), з прискоренням, обчисленим за законами динаміки (1). ВЛАСНОЇ ВАГИ Устаткування: похила площина, досліджуване тіло, метрова лінійка, секундомір. Теоретичний вступ
F = Р sin а = mg sin а (1) тягне його вздовж площини донизу, але руху заважає сила тертя Т — kN = kmg cos а, (2) де N = Р cos а- — нормальний тиск тіла на площину, k- коефіцієнт тертя, дещо більший у спокої — k0 і менший у русі — kp. При малих кутах а підйому площини переважає сила тертя Т і тіло залишається в спокої, при великих кутах а переважає сила, що тягне донизу, і тіло рухається. При пев- _____________________________________________________ ВИЗНАЧЕННЯ ШВИДКОСТІ КУЛІ Устаткування: пневматична рушниця на штативі,кулі,балістичний маятник,екран, терези з важками. Теоретичний вступ
Якщо куля з масою m ударяється в торець із швидкістю v і застряє в циліндрі, то кількість руху кулі mv стає спільною для циліндра і кулі. Припустимо, маса циліндра М, а його швидкість V. Тоді, розглядаючи кулю і підвішений циліндр як ізольовану систему, на основі закону збереження кількості руху маємо: mv = MV + mV = (m+M) V. Числові значення мас т і М легко визначити зважуванням кулі і циліндра. Проте швидкості їх невідомі. Таким чином, (1) являє собою одне рівняння з двома невідомими. Друге рівняння з тими самими невідомими легко скласти, використавши закон збереження енергії. Після удару кінетична енергія кулі з циліндром перетворюється в потенціальну (m + М) gh підняття циліндра з кулею на певну висоту h:
Розв’язуючи рівняння (1) і (2) сумісно і нехтуючи масою m як доданком спільної маси m + М, дістаємо V = Що ж до новоявленої величини h — висоти підняття циліндра, то її можна вимірювати різними методами, наприклад проектуванням певної точки циліндра на екран з гори - зонтальними лініями. Частіше, проте, користуються вимірюнням кута а відхилення підвісних дротин маятника від вертикалі (рис. 6). Якщо позначити віддаль центра ваги С циліндра від точки підвісу О через L, то з ∆ОВС' випливає, що OB = L — h і Підставляючи значення h у формулу (3), дістаємо: v = 2 Вважаючи рух кулі в дулі рушниці рівноприскореним, можна визначити середнє прискорення кулі за знайденим значенням швидкості v вильоту кулі з дула і довжиною шляху
де a = ЗА ДОПОМОГОЮ МАЯТНИКА
Теоретичний вступ
Маятник, кулька якого описує коло, а підвісна нитка - конус, називається конічним. Закономірності руху конічного маятника порівняно прості: кулька рухається по колу радіуса ад = w2r. (1) З рис. 7 видно, що ад виникає як горизонтальна складова прискорення g ваги кульки ад = g tg a. (2) З рівнянь (1) і (2) маємо, що
Оскільки w = маятника дорівнює Т = 2 Знання кутової швидкості (3) рівномірного руху конічного маятника робить можливим визначення положення кульки в довільний момент часу і за величиною її кутового переміщення φ відносно відлікового стану 0 φ = де Величину (5), що дає змогу визначати положення коливної точки в довільний момент часу,називають фазою коливання. Її величину виражають у радіанах або градусах. У зв’язку з повторністю її значення через кожні 2 З рис. 8 видно, що в момент х = r sin ( Якщо максимальне значення зміщення кульки О'К1 = О'К2 = х = A sin ( Коливання, при яких зміщення є синусоїдною або косину-соїдною функцією часу, називають гармонічними. Коливання математичного маятника є прикладом гармонічних коливань. Проекцією прискорення аа кульки конічного маятник на екран є прискорення а’a кульки маятника плоского (рис. 8), тому а'д = ад sin φ = ад sin ( Ураховуючи рівності (1), (6), а також ад = — З цієї формули видно, що при гармонічному коливанні прискорення пропорційне зміщенню і має протилежний йому напрям. Помноживши прискорення aд точки на її масу
Спроектувавши вектор швидкості точки Оскільки коливання плоского маятника можна розглядати як результат проектування на екран обертань конічного, то період коливань Т плоского маятника, як і конічного, можна обчислити за формулою (4). Слід, проте, мати, на увазі, що довжина плоского маятника З формули (4) видно, що від маси точки період коливань гль- маятника не залежить. • Прискорення g, а отже і сила, з якою Земля притягує (6) тіла,— вага тіла Р = mg, збільшується від екватора до полюса. Причини цього такі: зменшення віддалі до центра Землі (Земля має форму сплюснутої кулі) і обертання Землі навколо своєї осі. Але і в одному географічному місці Землі g залежить від висоти місця над рівнем моря і від густини та розміщення земних порід. Зменшення g з висотою легко врахувати, тому точні вимірювання g можуть дати цінну інформацію для розвідників земних надр про поклади корисних копалин. Метою цієї роботи є дослідне визначення прискорення g за допомогою формули g = 4 що випливає з рівняння (4). Оскільки в цю формулу Т входить у квадраті, то при обчисленні похибки результату похибка періоду подвоюватиметься. Секундомір забезпечує точність відліку не більш, як 0,2 с, тому вимірювання періоду стає вузьким місцем експерименту. Щоб похибка визначення прискорення була якомога меншою, треба період коливань визначати як середнє арифметичне з тривалості кількох десятків коливань маятника. Теоретичний вступ Газовий термометр — це прилад для вимірювання температури на основі закономірностей температурних змін пружності газу. За його допомогою вимірюють температуру в широкому інтервалі її значень у градусах Кельвіна ( Нагадаємо, що потрійною точкою води називається температура, при якій вода може існувати в трьох станах — твердому, рідкому і газовому, не проявляючи тенденції до перетворення в якийсь один. Цю температуру, відмінну від точки танення льоду всього на тисячні частки градуса, беруть за основну (реперну) точку В основу вимірювання температур покладено закон Шарля про пряму пропорційність термодинамічної температури і тиску газу при незмінності його маси та об’єму:
Закон Шарля є окремим випадком закону газового стану:
коли об’єм газу сталий. Якщо взяти до уваги реперність Т0 = 273,16 К, то рівняння (1) дає робочу формулу для вимірювання температури
де З реальних газів пропорційність (1) найкраще задовольняє водень. У навчальній роботі використовують повітря, просушене пропусканням через гігроскопічну речовину ( Сказаним в основному визначається і конструкція газового термометра, і метод вимірювання. Це має бути балон Якщо балон А занурити в танучий лід, то пружність його повітря знизиться і ртуть, витискувана з правого коліна
в Якщо перенести балон А з танучого льоду в пару киплячої води парогенератора (рис. 10), то збільшений у ньому тиск повітря витисне ртуть у лівому коліні донизу. Щоб відновити попередній об’єм газу за позначкою а, доведеться підняти праве коліно О вище від рівня ртуті над позначкою а, наприклад на її. Тоді той самий об’єм повітря перебуватиме при невідомій температурі Т кипіння води під тиском |
|
| Поделиться: |







 = 3,1416 при обмеженні двома знаками після коми.
= 3,1416 при обмеженні двома знаками після коми. = 3,1416 за точне, а 3,14 — за наближене, дістаємо похибку ∆
= 3,1416 за точне, а 3,14 — за наближене, дістаємо похибку ∆  =
= 
 100% = 0,06%.
100% = 0,06%. брати недоцільно.
брати недоцільно.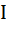 навіть без обчислень видно, що з точністю до трьох значущих цифр (тобто до сотих) значення
навіть без обчислень видно, що з точністю до трьох значущих цифр (тобто до сотих) значення 
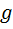 з таким заокругленим значенням
з таким заокругленим значенням 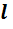 і прискорення вільного падіння g зв'язані формулою.
і прискорення вільного падіння g зв'язані формулою.

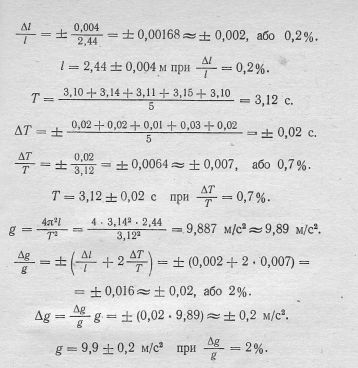
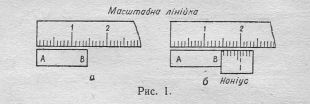
 мм і з точністю до
мм і з точністю до  мм.
мм.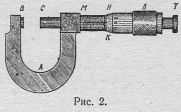 При цьому нульова поділка барабана буде проти масштабної лінійки //.
При цьому нульова поділка барабана буде проти масштабної лінійки //. Прилад Атвуда складається з високого вертикального стояка (рис. 3), який має на верхньому кінці блок Б, що має обертатися з малим тертям. Якщо до кінців гнучкої нитки, перекинутої через блок, підвісити важки Р1 і Р2 однакової маси т, то в полі земного тяжіння вся система важків з ниткою буде в рівновазі. Від короткого імпульсу руки система набуде певної швидкості і, рухаючись за інерцією, зберігатиме її сталою згідно з першим законом динаміки (в міру можливості нехтувати тертям).
Прилад Атвуда складається з високого вертикального стояка (рис. 3), який має на верхньому кінці блок Б, що має обертатися з малим тертям. Якщо до кінців гнучкої нитки, перекинутої через блок, підвісити важки Р1 і Р2 однакової маси т, то в полі земного тяжіння вся система важків з ниткою буде в рівновазі. Від короткого імпульсу руки система набуде певної швидкості і, рухаючись за інерцією, зберігатиме її сталою згідно з першим законом динаміки (в міру можливості нехтувати тертям). .
. (1)
(1)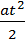 (2)
(2) ,а швидкість у кінці першої секунди v1 чисельно дорівнює прискоренню (v = а). Об’єднуючи ці два висновки, дістанемо чисельну рівність:
,а швидкість у кінці першої секунди v1 чисельно дорівнює прискоренню (v = а). Об’єднуючи ці два висновки, дістанемо чисельну рівність: На тіло масою m (рис. 4), що перебуває на похилій площині АВ, діє сила його ваги Р = mg і сила тертя з площиною Т. Складова сили ваги;
На тіло масою m (рис. 4), що перебуває на похилій площині АВ, діє сила його ваги Р = mg і сила тертя з площиною Т. Складова сили ваги; Балістичний маятник являє собою масивне тіло, підвішене на легких нерозтяжних дротинах. У розглядуваному випадку (рис. 6) — це циліндр, заповнений пластиліном на двох двониткових підвісах, я дають можливість йому при ударі в торець рухатись лише поступально.
Балістичний маятник являє собою масивне тіло, підвішене на легких нерозтяжних дротинах. У розглядуваному випадку (рис. 6) — це циліндр, заповнений пластиліном на двох двониткових підвісах, я дають можливість йому при ударі в торець рухатись лише поступально.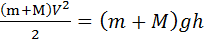 (2)
(2) (3)
(3) =
=  cos a. Звідси h — L (1 — cos а) = 2 L sin2
cos a. Звідси h — L (1 — cos а) = 2 L sin2  .
. sin
sin  . (4)
. (4)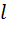 її в дулі рушниці за законами кінематики
її в дулі рушниці за законами кінематики і
і  = at =
= at = 
 — тривалість руху кулі в дулі. Це дає
— тривалість руху кулі в дулі. Це дає ,
, 
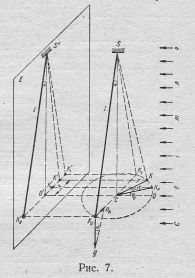 »Кожне тіло, підвішене в точці, що не збігається з йо центром ваги, можна розглядати як коливну систему, яка називається маятником. Найпростішим з них є колив система з матеріальної точки (кульки), підвішеної на тонкій нерозтяжній ї невагомій нитці,— математичний маятник. Якщо відхилити його кульку від положення рівноваги SC (рис. 7) і без жодного поштовху відпустити, то вона ковзатиметься в одній площині, наприклад, уздовж К1СК2.Як що ж відпустити кульку з бічним поштовхом, перпендикулярним до попередньої площини, то при певних умовах кулька почне рівномірно обертатись по колу 0 КоКК1К2..., а підвісна нитка її описуватиме конічну поверхню. Маятник, кулька якого з підвісною ниткою коливається в одній площині, називається плоским.
»Кожне тіло, підвішене в точці, що не збігається з йо центром ваги, можна розглядати як коливну систему, яка називається маятником. Найпростішим з них є колив система з матеріальної точки (кульки), підвішеної на тонкій нерозтяжній ї невагомій нитці,— математичний маятник. Якщо відхилити його кульку від положення рівноваги SC (рис. 7) і без жодного поштовху відпустити, то вона ковзатиметься в одній площині, наприклад, уздовж К1СК2.Як що ж відпустити кульку з бічним поштовхом, перпендикулярним до попередньої площини, то при певних умовах кулька почне рівномірно обертатись по колу 0 КоКК1К2..., а підвісна нитка її описуватиме конічну поверхню. Маятник, кулька якого з підвісною ниткою коливається в одній площині, називається плоским. з доцентровим прискоренням
з доцентровим прискоренням = g tg а. Але а = тому величина кутової швидкості кульки буде
= g tg а. Але а = тому величина кутової швидкості кульки буде (3)
(3) ,то період обертання (коливання) Т конічного
,то період обертання (коливання) Т конічного (4)
(4) 0, (5)
0, (5) — кутове переміщення кульки протягом часу руху t; φо — початкове кутове переміщення кульки на час t = 0.Закономірності руху кульки
— кутове переміщення кульки протягом часу руху t; φо — початкове кутове переміщення кульки на час t = 0.Закономірності руху кульки  плоского маятника легко визначити проектуванням (наприклад, бічним підсвічуванням паралельними променями) руху кульки
плоского маятника легко визначити проектуванням (наприклад, бічним підсвічуванням паралельними променями) руху кульки 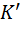 кульки плоского. Оскільки ж положення
кульки плоского. Оскільки ж положення  радіан додавання чи віднімання до фази величин 2
радіан додавання чи віднімання до фази величин 2  n (n — ціле число) не змінює величини фази. Тому φ =
n (n — ціле число) не змінює величини фази. Тому φ = 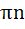 =
=  . (9)
. (9) , дістанемо вираз для сили F, що повертає зміщену точку в положення рівноваги:
, дістанемо вираз для сили F, що повертає зміщену точку в положення рівноваги:
 на екран, можна знайти вираз для швидкості (а за ним і енергії) точки К’ при гармонічних коливаннях.
на екран, можна знайти вираз для швидкості (а за ним і енергії) точки К’ при гармонічних коливаннях. cos а. Тому
cos а. Тому  =
=  2
2  (10)
(10) частинах термодинамічної температури потрійної точки води.
частинах термодинамічної температури потрійної точки води. = 273,16 К.
= 273,16 К.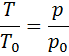

 за відомими тисками
за відомими тисками 
 (2)
(2) і
і  — тиски газу, що відповідають «початковій»
— тиски газу, що відповідають «початковій»  і вимірюваній
і вимірюваній 
 (рис. 9) з повітрям (термометричним тілом), сполучений і манометром С — D для вимірювання тисків і для регулювання сталості об’ємів газу. Ці обидві функції можна сумістити у відкритому ртутному манометрі, якщо його комі па
(рис. 9) з повітрям (термометричним тілом), сполучений і манометром С — D для вимірювання тисків і для регулювання сталості об’ємів газу. Ці обидві функції можна сумістити у відкритому ртутному манометрі, якщо його комі па  і D сполучити гнучким шлангом, щоб переміщати одне коліно вгору або донизу незалежно від положення другого. Ртуть, яка міститься в колінах і шланзі, у такому разі буде джерелом потрібних тисків на повітря в резервуарі і водночас даватиме змогу встановлювати потрібний сталий об’єм газу за позначкою а на стінці коліна
і D сполучити гнучким шлангом, щоб переміщати одне коліно вгору або донизу незалежно від положення другого. Ртуть, яка міститься в колінах і шланзі, у такому разі буде джерелом потрібних тисків на повітря в резервуарі і водночас даватиме змогу встановлювати потрібний сталий об’єм газу за позначкою а на стінці коліна  .
. атмосферним тиском
атмосферним тиском 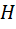 і різницею рівнів ртуті в колінах
і різницею рівнів ртуті в колінах  нижче від
нижче від  . У цьому стані повітря
. У цьому стані повітря

 .
.


