
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Про вимірювання фізичних величин та похибкиСодержание книги
Поиск на нашем сайте
Точні виміри є важливою частиною фізичного експерименту. Жодне вимірювання не може бути абсолютно точним, оскільки з кожним пов’язана деяка похибка. Джерела виникнення цієї похибки різні. До найважливіших належать обмежена точність будь-якого вимірювального приладу, а також неможливість зчитування з його шкали показів менших, ніж мінімальна ціна поділки. Помилки вимірювань бувають і суб’єктивного характеру. Вони можуть виникати з вини експериментатора – від недосконалості зору, слуху або з інших причин, які неможливо врахувати заздалегідь. Випадкові помилки можуть змінювати результати як в більший, так і в менший боки. Визначення похибки прямих вимірювань. Нехай
є величина, найближча до істинного значення. Вона називається середнім значенням. Різниці
називаються абсолютними похибками і можуть бути як додатними, так і від’ємними. Для визначення середньої абсолютної похибки результату беруть середнє арифметичне абсолютних значень (модулів) окремих помилок, тобто
Відношення Відношення середньої абсолютної похибки результату
Відносну похибку прийнято виражати у відсотках
Істинне значення величини, яку вимірювали, записують у вигляді:
І. СТЕНДОВІ ЛАБОРАТОРНІ РОБОТИ
ФІЗИЧНІ ОСНОВИ МЕХАНІКИ. МЕХАНІЧНІ КОЛИВАННЯ
ЛАБОРАТОРНА РОБОТА №1.1 ВИМІРЮВАННЯ ЛІНІЙНИХ ВЕЛИЧИН Мета роботи: навчитися використовувати штангенциркуль та мікрометр на практиці. Прилади: штангенциркуль, мікрометр, предмети для вимірювання.
ТЕОРЕТИЧНІ ВІДОМОСТІ Для вимірювання лінійних та кутових величин користуються різноманітними приладами та інструментами. Найпростіші з них: штангенциркуль, мікрометр, мікроскоп, кутомір та ін. Довжини вимірюють масштабними лінійками, рулетками. Величина найменшої поділки такої лінійки зветься ціною однієї поділки. Зазвичай ціна однієї поділки лінійки рівна 1 мм. Перша риска вважається нулем (нульова риска). Якщо вимірювання проводять з точністю до долі міліметра, то користуються допоміжною шкалою вимірювального інструмента – ноніусом. Ноніус буває лінійний – для вимірювання лінійних величин, та кутовий – для вимірювання кутових величин. Штангенциркуль Лінійний ноніус є невеликою лінійкою С зі шкалою, m поділок якої дорівнюють m – 1 поділкам шкали масштабної лінійки А. Ноніус С можна переміщувати по лінійці А (рис. 1.1.1).
Отримана з формули (1.1.1) різниця  називається точністю ноніуса, тобто точність ноніуса називається точністю ноніуса, тобто точність ноніуса  рівна відношенню ціни найменшої поділки масштабної лінійки до кількості поділок на ноніусі. Точність ноніуса часто буває 1/10 мм або 1/20 мм. рівна відношенню ціни найменшої поділки масштабної лінійки до кількості поділок на ноніусі. Точність ноніуса часто буває 1/10 мм або 1/20 мм.
Виміри за допомогою ноніуса виконують так: до нульової риски шкали лінійки прикладають один кінець вимірюваного тіла В, до другого кінця – ноніус С (рис. 1.1.2) З рис. 1.1.2 бачимо, що шукана довжина тіла В (заштрихованого на рис. 1.1.2)
де k – ціле число поділок масштабної лінійки в мм, яке вкладається у вимірювану довжину; Визначаємо, які поділки ноніуса та лінійки збігаються. Позначаємо n той номер поділки ноніуса, який збігається з певною поділкою масштабної лінійки, тоді
З формули (1.1.2) і (1.1.3) знаходимо шукану довжину
Якщо припустити
Отже, довжина вимірюваного тіла рівна цілому числу k мм масштабної лінійки плюс n десятих часток мм. З рис. 1.1.2 видно, що:
Штангенциркуль (рис. 1.1.3) складається зі сталевої міліметрової лінійки А, з одного кінця якої є нерухома ніжка В. Друга ніжка D має ноніус С і може переміщатись вздовж лінійки А. Коли ніжки В і D стискаються, нуль лінійки і нуль ноніуса мають збігатися. Для того, щоб виміряти довжину предмета М, його розміщують між ніжками, які торкаються предмета М (без сильного натиску), і закріплюють положення рухомої ніжки гвинтом Е. Після цього знімають покази на лінійці і ноніусі та розраховують розміри предмета М за формулою (1.1.4). Мікрометр Мікрометричний гвинт використовується у вимірювальних приладах вищої точності (мікрометр, мікроскоп) і дає можливість визначати розміри тіл до сотої частки міліметра. Мікрометричний гвинт являє собою стрижень, який має точну гвинтову нарізку. Висота підйому гвинтової нарізки за один оберт називається кроком мікрометричного гвинта.
Для того, щоб мікрометричний гвинт А перемістився на 1 мм, необхідно зробити два оберти барабана С. Таким чином, крок мікрометричного гвинта дорівнює 0,5 мм. У мікрометрі на барабані С є шкала, яка має 50 поділок. Якщо крок гвинта
Для вимірювання мікрометром предмет поміщають між упором Е і мікрометричним гвинтом А (рис. 1.1.4) і обертають гвинт А за головку М до тих пір, поки вимірюваний предмет не буде затиснутий між упором Е і кінцем гвинта А (гвинт А обертають тільки за головку М, тому що в іншому випадку легко збити збіг нулів шкали стебла D і барабана С). Довжину
де На рис. 1.1.5 маємо
ПОРЯДОК ВИКОНАННЯ РОБОТИ
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 491; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 ,
,  ,
,  ,...,
,...,  – результати окремих вимірювань фізичної величини,
– результати окремих вимірювань фізичної величини,  – число окремих вимірювань. Середнє арифметичне цих результатів
– число окремих вимірювань. Середнє арифметичне цих результатів
 ;
;  ;
;  ;...;
;...;  між середнім значенням
між середнім значенням  величини, що вимірюємо, і значеннями
величини, що вимірюємо, і значеннями 
 .
.
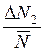 ,
, 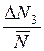 ,...,
,..., 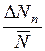 називають відносними помилками окремих вимірювань.
називають відносними помилками окремих вимірювань. до його середнього значення
до його середнього значення 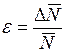 .
. %.
%. .
.


 .
.

 ,
,
 – відрізок довжини, який є часткою міліметра.
– відрізок довжини, який є часткою міліметра. .
.
 .
.
 мм,
мм,  поділок, то шукана довжина
поділок, то шукана довжина мм.
мм.
 мм
мм  мм, оскільки
мм, оскільки  мм,
мм,  .
.
 Мікрометр (рис. 1.1.4 і 1.1.5) складається з двох основних частин: скоби В і мікрометричного гвинта А. Мікрометричний гвинт А проходить крізь отвір скоби В з внутрішньою різьбою. Напроти мікрометричного гвинта, на скобі, є упор Е. На мікрометричному гвинті закріплений порожнистий циліндр (барабан) С з поділками по колу. Під час обертання мікрометричного гвинта барабан ковзає по лінійній шкалі, нанесеній на стеблі D.
Мікрометр (рис. 1.1.4 і 1.1.5) складається з двох основних частин: скоби В і мікрометричного гвинта А. Мікрометричний гвинт А проходить крізь отвір скоби В з внутрішньою різьбою. Напроти мікрометричного гвинта, на скобі, є упор Е. На мікрометричному гвинті закріплений порожнистий циліндр (барабан) С з поділками по колу. Під час обертання мікрометричного гвинта барабан ковзає по лінійній шкалі, нанесеній на стеблі D. Найбільш розповсюджений мікрометр з ціною поділки лінійної шкали стебла
Найбільш розповсюджений мікрометр з ціною поділки лінійної шкали стебла  мм. Верхні і нижні риски шкали зсунуті одна відносно одної на половину міліметра; цифри проставлені тільки для поділок нижньої шкали (рис. 1.1.5).
мм. Верхні і нижні риски шкали зсунуті одна відносно одної на половину міліметра; цифри проставлені тільки для поділок нижньої шкали (рис. 1.1.5). мм, а число поділок барабана
мм, а число поділок барабана  , то точність мікрометра складає:
, то точність мікрометра складає:
 предмета знаходять за формулою
предмета знаходять за формулою ,
,
 – число найменших поділок шкали,
– число найменших поділок шкали,  – ціна найменшої поділки шкали,
– ціна найменшої поділки шкали,  – число всіх поділок на шкалі барабана,
– число всіх поділок на шкалі барабана,  мм
мм  мм
мм  мм.
мм.


