
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення відношення питомих теплоємностей газу методом адіабатичного розширенняСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Мета роботи: визначити відношення питомих теплоємностей газу методом адіабатичного розширення. Прилади: закритий скляний балон, манометр, насос.
ТЕОРЕТИЧНІ ВІДОМОСТІ Експериментальна установка складається зі скляного балона А (рис. 1.8.1), з’єднаного з манометром В і з насосом. За допомогою крану С балон А може з’єднуватись із атмосферою. Якщо закрити кран С і за допомогою насоса нагнітати в балон деяку кількість повітря, то тиск та температура повітря всередині балона підвищаться. За рахунок теплообміну із зовнішнім середовищем через деякий час температура повітря у балоні зрівняється із температурою зовнішнього середовища Тиск, що встановився у балоні
де H – атмосферний тиск; Отже, стан повітря всередині балона, який назвемо І-им станом, характеризується параметрами
Якщо відкрити на короткий час кран С, то з балона буде виходити повітря, переходячи із стиснутого стану в розширений. Цей процес можна вважати адіабатичним. Коли тиск у балоні зрівняється з атмосферним H, температура газу знизиться до, а об’єм буде рівний. Тоді, в кінці адіабатичного процесу, що назвемо ІІ-им станом, параметри будуть: H; і Застосовуючи до І-го і ІІ-го станів рівняння
Охолоджене під час розширення повітря у балоні через деякий час внаслідок теплообміну нагріється до температури зовнішнього середовища
де Отож цей стан повітря, який назвемо ІІІ-ім станом, характеризується параметрами
У І-му і ІІІ-му станах повітря має однакову температуру (процес ізотермічний), тому застосовуємо закон Бойля-Маріотта (
Підносячи обидві частини рівняння (1.8.2) до степеня
і користуючись виразами (1.8.1) і (1.8.2), отримуємо, що
Логарифмуючи останній вираз і розв’язуючи його відносно
Оскільки тиски H,
ВИМІРЮВАНЛЬНА УСТАНОВКА І МЕТОДИКА ВИМІРЮВАНЬ 1. Переконавшись у тому, що кран С закритий, за допомогою насосу обережно нагнітають повітря у балон доти, доки різниця рівнів рідини у манометрі не досягне 60 – 100 мм. 2. Коли тиск у балоні стабілізується, про що свідчить припинення коливання рівнів у колінах манометра, за шкалою визначають різницю рівнів рідини у манометрі 3. Швидко відкривають кран С і негайно (як тільки рівні рідини у колінах зрівняються) його закривають. Коли тиск остаточно встановиться, вдруге вимірюють рівні рідини у колінах манометра 4. Дослід повторюють 5 – 7 разів, змінюючи у манометрі величину 5. Підставляючи у формулу (1.8.4) значення 6. Усі отримані результати вимірювань заносять у таблицю 1.8.1. 7. Визначають середні значення отриманих величин, відносну та абсолютну похибки.
Таблиця 1.8.1
КОНТРОЛЬНІ ЗАПИТАННЯ
1. Дати визначення адіабатичного процесу. 2. У чому полягає метод адіабатичного розширення (метод Клемана-Дезорма)? 3. Який зв’язок між питомою і молярною теплоємністю будь-якої речовини? 4. Сформулювати перше начало термодинаміки. 5. Записати рівняння стану для ідеальних газів. 6. Вивести рівняння Пуассона.
ЛАБОРАТОРНА РОБОТА №1.9
ВИЗНАЧЕННЯ СЕРЕДНЬОЇ ДОВЖИНИ ВІЛЬНОГО ПРОБІГУ І ЕФЕКТИВНОГО ДІАМЕТРА МОЛЕКУЛ ПОВІТРЯ З ВИМІРЮВАНЬ КОЕФІЦІЄНТА ВНУТРІШНЬОГО ТЕРТЯ
Мета роботи: визначити довжини вільного пробігу і ефективний діаметр молекул повітря з вимірювань його коефіцієнта внутрішнього тертя. Прилади: посудина з краном у нижній частині і капіляром, пропущеним через верхній корок, мензурка, секундомір, термометр. ТЕОРЕТИЧНІ ВІДОМОСТІ Для вимірювання коефіцієнта внутрішнього тертя можна скористатися методом протікання рідини або газу через вузьку капілярну трубку. Об’єм газу V, що протік в трубці з круглим внутрішнім перерізом за час
де r – радіус капіляра; l – довжина капіляра; Використавши рівняння (1.9.1), коефіцієнт внутрішнього тертя можна виразити співвідношенням
в якому всі величини правої частини вимірюються безпосередньо і ними можна скористатися для експериментального визначення коефіцієнта внутрішнього тертя газу. Кінетична теорія газів встановлює зв’язок між коефіцієнтом внутрішнього тертя ідеальних газів
де
Замінивши в цьому рівнянні
де Т – абсолютна температура; R – універсальна газова стала;
де n – число молекул в одиниці об’єму. Із (1.9.6) можна визначити ефективний діаметр молекул газу за даної температури, якщо відомі
де
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 446; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.6.9 (0.011 с.) |

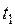 .
. ,
, – додатковий тиск, який вимірюється манометром і дорівнює різниці рівнів рідини в манометрі.
– додатковий тиск, який вимірюється манометром і дорівнює різниці рівнів рідини в манометрі. ;
;  і.
і. .
. (рівняння Пуассона), отримаємо:
(рівняння Пуассона), отримаємо: ,
, 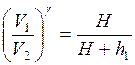 .
.
 ,
, – нова різниця рівнів у манометрі; об’єм повітря не зміниться і буде рівним
– нова різниця рівнів у манометрі; об’єм повітря не зміниться і буде рівним 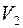 .
. ;
;  і
і 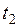 .
.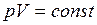 ):
): ,
, .
.
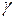

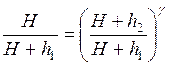 .
. , знаходимо:
, знаходимо: .
. і
і  мало чим відрізняються один від одного, то різниці логарифмів можна вважати пропорційними різницям тисків. Тоді коефіцієнт Пуассона
мало чим відрізняються один від одного, то різниці логарифмів можна вважати пропорційними різницям тисків. Тоді коефіцієнт Пуассона  ,
,  .
.
 ,
,  ,
,  і т.д.
і т.д.

 , визначається формулою Пуазейля
, визначається формулою Пуазейля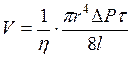 ,
,
 – різниця тисків на кінцях капіляра, яка зумовлює рух газу.
– різниця тисків на кінцях капіляра, яка зумовлює рух газу. ,
,
 , середньою довжиною вільного пробігу молекул газу
, середньою довжиною вільного пробігу молекул газу  і середньою швидкістю їх руху
і середньою швидкістю їх руху  у вигляді
у вигляді ,
,
 – густина газу. Більш точне виведення співвідношення (1.9.3), що враховує розподіл швидкостей молекул згідно із законом Максвелла, дає інше значення коефіцієнта пропорційності. Так, для повітря співвідношення (1.9.3) набуває вигляду
– густина газу. Більш точне виведення співвідношення (1.9.3), що враховує розподіл швидкостей молекул згідно із законом Максвелла, дає інше значення коефіцієнта пропорційності. Так, для повітря співвідношення (1.9.3) набуває вигляду .
.
 ,
,
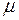 – молекулярна маса газу. Середня довжина вільного пробігу
– молекулярна маса газу. Середня довжина вільного пробігу  пов’язані співвідношенням
пов’язані співвідношенням ,
,
 ,
,
 – число молекул в 1
– число молекул в 1  за нормальних умов (
за нормальних умов ( ;
;  ), яке називається числом Лошмідта. Враховуючи (1.9.6) і (1.9.7),
), яке називається числом Лошмідта. Враховуючи (1.9.6) і (1.9.7),  .
.



