
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Опис вимірювальної установки іСодержание книги
Поиск на нашем сайте
МЕТОДИКА ВИМІРЮВАНЬ
На рис. 1.2.1 показано математичний маятник. Ниткою задають певну довжину Із закону всесвітнього тяжіння Ньютона
ПОРЯДОК ВИКОНАННЯ РОБОТИ
1. Виміряти довжину математичного маятника 2. Для знайденої довжини визначити час 20 – 100 повних коливань і підрахувати період коливань 3. Змінити довжину маятника, визначити період. Вимірювання повторити не менше 3-х разів. 4. Обчислити прискорення земного тяжіння g за формулою (1.2.4). 5. Визначити масу та густину Землі (1.2.5). 6. Розрахувати абсолютні та відносні похибки визначення
7. Всі обчислені і виміряні величини занести в таблицю 1.2.1:
Таблиця 1.2.1
КОНТРОЛЬНІ ЗАПИТАННЯ 1. Що таке прискорення і сила? 2. Сформулювати ІІ-й закон Ньютона. 3. Сформулювати закон всесвітнього тяжіння. 4. Вивести рівняння гармонічного коливного руху математичного маятника. 5. Дати визначення параметрів коливного руху: амплітуди, фази, частоти, періоду. 6. Як залежить прискорення вільного падіння від географічної широти? ЛАБОРАТОРНА РОБОТА №1.3 ПЕРЕВІРКА ОСНОВНОГО РІВНЯННЯ ОБЕРТАЛЬНОГО РУХУ ЗА ДОПОМОГОЮ МАЯТНИКА МАКСВЕЛЛА
Мета роботи: перевірити основне рівняння динаміки обертального руху шляхом зіставлення прискорення, знайденого з основного рівняння обертального руху, і рівняння рівноприскореного руху маятника.
Прилади: маятник Максвелла, штангенциркуль, ваги (терези), секундомір.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Основний закон динаміки обертального руху твердого тіла, для якого
де Момент сили відносно нерухомої осі чисельно дорівнює добутку сили на її плече, тобто найкоротшу відстань від осі обертання до лінії дії сили. Момент інерції тіла відносно будь-якої осі дорівнює сумі моментів інерції всіх матеріальних точок тіла відносно цієї осі
де
ОПИС ВИМІРЮВАЛЬНОЇ УСТАНОВКИ І МЕТОДИКА ВИМІРЮВАНЬ
Запишемо рівняння поступального руху маховика в проекції на вертикальну вісь:
де Р – сила тяжіння маятника; Т – сила натягу нитки; m – маса маятника; а – прискорення центра тяжіння валика. Рівняння обертального руху маятника запишеться
де J – момент інерції маятника, Прискорення центра мас пов’язане з кутовою швидкістю співвідношенням
Розв’язавши рівняння (1.3.1), (1.3.2), (1.3.3) відносно прискорення центра мас, знаходимо:
Прискорення а можна також визначити з рівняння рівноприскореного поступального руху маятника:
де S – шлях, що пройшов центр мас маятника із верхнього крайнього положення в нижнє; t – час одного повного розкручування маятника. Відомо, що величина прискорення і сили тяжіння не залежать від напрямку руху маятника (вгору чи вниз). Під час коливань маятника швидкість змінює свій знак, а прискорення не змінює, як і рівнодійна сила.
ПОРЯДОК ВИКОНАННЯ РОБОТИ 1. Зважити маятник (валик і диск) m. 2. Визначити масу валика за формулою 3. Знайти масу диска за формулою 4. Розрахувати момент інерції маятника 5. Виміряти значення S і t. 6. Обчислити за (1.3.4) і (1.3.5) прискорення центру мас маятника (не менше трьох значень). 7. Розрахувати абсолютну і відносну похибки. 8. Порівняти 9. Всі виміряні і підраховані величини занести в таблицю 1.3.1.
Таблиця 1.3.1
КОНТРОЛЬНІ ЗАПИТАННЯ 1. Що таке момент сили і момент інерції? 2. Що таке кутова швидкість і кутове прискорення? 3. Дати визначення центра мас. 4. Вивести основне рівняння динаміки обертального руху. 5. Записати рівняння поступального і обертального руху маятника. 6. Як перевіряється основне рівняння динаміки обертального руху?
ЛАБОРАТОРНА РОБОТА №1.4 ВИЗНАЧЕННЯ ПОТЕНЦІАЛЬНОЇ ТА КІНЕТИЧНОЇ ЕНЕРГІЇ КУЛЬКИ
Мета роботи: перевірити закон збереження енергії кульки. Прилади: прилад Грімзеля, лінійка, стальна кулька, ванночка з піском. ТЕОРЕТИЧНІ ВІДОМОСТІ
Енергія – фізична величина, яка характеризує здатність тіла або системи тіл здійснювати роботу. Вона вимірюється кількістю роботи, яку за певних умов може здійснити система тіл. До механічної енергії відносять два види енергії – кінетичну
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 288; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.165.234 (0.006 с.) |

 математичного маятника, фіксуючи її. Відводять кульку вбік
математичного маятника, фіксуючи її. Відводять кульку вбік  , заміряють час t, за який здійснюється 20 – 100 коливань, визначають час одного коливання – період
, заміряють час t, за який здійснюється 20 – 100 коливань, визначають час одного коливання – період  . Такі ж виміри повторюють для другої довжини
. Такі ж виміри повторюють для другої довжини  . Вимірювання повторюють не менше 3-х разів.
. Вимірювання повторюють не менше 3-х разів. , де
, де  – маса Землі,
– маса Землі,  – радіус Землі в даному місці (прийняти
– радіус Землі в даному місці (прийняти  км), G – гравітаційна стала
км), G – гравітаційна стала  обчислюють масу Землі. За підрахованою масою і знайденим об’ємом Землі визначають густину Землі
обчислюють масу Землі. За підрахованою масою і знайденим об’ємом Землі визначають густину Землі  .
. ;
; 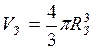 ;
;  . (1.2.5)
. (1.2.5) .
. та
та  ;
;  .
.

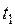 , с
, с
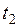 , с
, с
 , с
, с
 , с
, с


 , запишеться
, запишеться ,
, – сума моментів усіх сил, які діють на систему; J – момент інерції тіла;
– сума моментів усіх сил, які діють на систему; J – момент інерції тіла;  – кутове прискорення,
– кутове прискорення,  – кут повороту,
– кут повороту,  – час повороту.
– час повороту.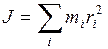 ,
,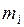 – маса і -тої матеріальної точки,
– маса і -тої матеріальної точки,  – відстань від і -тої матеріальної точки до осі обертання.
– відстань від і -тої матеріальної точки до осі обертання.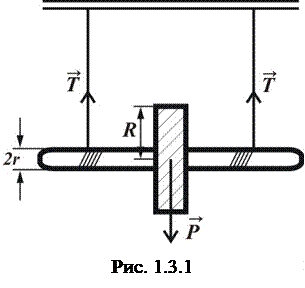 Невеликий диск (маховичок), насаджений на вісь, опускається під дією сили тяжіння на двох нитках, які розмотуються на всю довжину. Маховик продовжує обертальний рух у зворотному напрямку, в результаті чого сам підіймається вгору, і при цьому гальмує свій рух. Дійшовши до верхньої точки, диск знову опускатиметься вниз і т.д. Маховик здійснюватиме коливання вгору і вниз, тому він і називається маятником. На рис. 1.3.1 зображений маятник Максвелла.
Невеликий диск (маховичок), насаджений на вісь, опускається під дією сили тяжіння на двох нитках, які розмотуються на всю довжину. Маховик продовжує обертальний рух у зворотному напрямку, в результаті чого сам підіймається вгору, і при цьому гальмує свій рух. Дійшовши до верхньої точки, диск знову опускатиметься вниз і т.д. Маховик здійснюватиме коливання вгору і вниз, тому він і називається маятником. На рис. 1.3.1 зображений маятник Максвелла. ,
,
 ,
,
 – кутове прискорення,
– кутове прискорення,  – кутова швидкість, r – радіус валика. Момент інерції маятника складається з моменту інерції валика і диска. Причому, момент інерції валика рівний
– кутова швидкість, r – радіус валика. Момент інерції маятника складається з моменту інерції валика і диска. Причому, момент інерції валика рівний  , а момент інерції диска має вигляд:
, а момент інерції диска має вигляд:  , де
, де  – маса валика,
– маса валика,  – маса диска, R – радіус диска.
– маса диска, R – радіус диска. .
.
 .
.
 ,
,
 , де V – об’єм валика;
, де V – об’єм валика;  – густина матеріалу; l – довжина валика.
– густина матеріалу; l – довжина валика.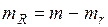 .
. .
. та
та  . Зробити висновок.
. Зробити висновок. , кг
, кг

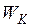 і потенціальну
і потенціальну  . Якщо відсутнє розсіювання енергії системи і взаємодія відбувається за допомогою консервативних сил, то сума кінетичної і потенціальної енергії в усіх проміжних точках шляху залишається незмінною
. Якщо відсутнє розсіювання енергії системи і взаємодія відбувається за допомогою консервативних сил, то сума кінетичної і потенціальної енергії в усіх проміжних точках шляху залишається незмінною  .
.


