
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вимірювання штангенциркулем іСодержание книги
Поиск на нашем сайте Обробка результатів вимірів Штангенциркулем вимірюють висоту h і діаметр d циліндра. Виміри проводять так: 1. Циліндр розміщують між ніжками B і D штангенциркуля (легко торкаючись його) і закріплюють гвинт рухомої ніжки гвинтом Е. 2. Вимірюють довжину і діаметр циліндра, проводячи за шкалою лінійки А відлік кількості цілих міліметрів k, розташованих зліва від нульової поділки ноніуса і кількості поділок n шкали ноніуса. За формулою (1.1.4) роблять підрахунки. Виміри проводять три рази, трохи прокручуючи циліндр між ніжками. 3. Розраховують абсолютну і відносну похибки вимірювань. Результати вимірювань та розрахунків заносять у таблиці 1.1.1 і 1.1.2. Таблиця 1.1.1
Таблиця 1.1.2
Вимірювання мікрометром і Обробка результатів вимірів
1. Предмет, який потрібно виміряти (товстий дріт або металева пластинка), поміщають між упором Е і кінцем мікрометричного гвинта А. 2. Знаходять значення k і n на шкалі стебла D і барабана С. За формулою (1.1.6) підраховують шукану величину. 3. Виміри діаметра дроту 4. Обчислюють абсолютну і відносну похибки вимірів. Результати вимірювань та обчислень заносять у таблиці 1.1.3 і 1.1.4. Таблиця 1.1.3
Таблиця 1.1.4
КОНТРОЛЬНІ ЗАПИТАННЯ 1. Для чого використовується ноніус? Які бувають ноніуси? 2. Ціна поділки ноніуса штангенциркуля, мікрометра. 3. Пояснити методику вимірювань. 4. Що значить абсолютна і відносна похибки? Яка різниця між ними? 5. Дійсне значення вимірюваної величини. Як воно записується? ЛАБОРАТОРНА РОБОТА № 1.2
ВИЗНАЧЕННЯ ПРИСКОРЕННЯ ВІЛЬНОГО ПАДІННЯ І ГУСТИНИ ЗЕМЛІ ЗА ДОПОМОГОЮ МАТЕМАТИЧНОГО МАЯТНИКА
Мета роботи: використовуючи гармонічні коливання математичного маятника, визначити прискорення вільного падіння та густину Землі. Прилади: математичний маятник, секундомір, лінійка.
ТЕОРЕТИЧНІ ВІДОМОСТІ
Коливаннями або коливальними рухами називаються рухи або зміни стану, що повторюються з часом. Коливання бувають різними за своєю фізичною природою: механічні коливання тіла, підвішеного на пружині (пружинний маятник); гойдання маятників; коливання струн; вібрація фундаментів конструкцій; електромагнітні коливання тощо. Коливання називаються періодичними, якщо значення фізичних величин, які змінюються в процесі коливань, повторюються через рівний проміжок часу. Періодом коливань Частотою періодичних коливань
Циклічною (круговою) частотою періодичних коливань називається число повних коливань, що здійснюються за
Математичний маятник – це прилад, що складається з металевої кулі, яка підвішена на тонкій довгій нерозтяжній нитці (масою нитки можна знехтувати). Для невеликих кутів відхилення
Перед силою F стоїть мінус, оскільки вона напрямлена проти додатного напрямку координати зміщення x. Рівняння (1.2.1) можна записати, якщо
На рис. 1.2.1 показано напрямки цих сил. Періодичні коливання – це гармонічні коливання, у яких фізична величина
де тоді
Період коливань математичного маятника у цьому випадку визначається:
де Досліди для визначення прискорення вільного падіння проводять для різних довжин маятника. Для двох різних довжин маятника
Отже, для визначення прискорення
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 492; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 , мм
, мм

 , мм
, мм






 Середнє
значення
Середнє
значення


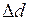 , мм
, мм

 , мм
, мм




 Середнє
значення
Середнє
значення



 і товщини пластинки
і товщини пластинки  повторюють не менше трьох разів у різних місцях.
повторюють не менше трьох разів у різних місцях. , мм
, мм
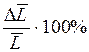
 , мм
, мм





 Середнє
значення
Середнє
значення


 h, мм
h, мм





 Середнє
значення
Середнє
значення


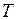 називається той найменший проміжок часу, через який повторюються значення всіх величин, які характеризують коливальні рухи. За цей час здійснюється одне повне коливання.
називається той найменший проміжок часу, через який повторюються значення всіх величин, які характеризують коливальні рухи. За цей час здійснюється одне повне коливання. називається число повних коливань, які здійснюються за одиницю часу:
називається число повних коливань, які здійснюються за одиницю часу:
 одиниць часу:
одиниць часу: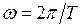 , тоді
, тоді  .
. рух такого маятника є прикладом гармонічного коливного руху матеріальної точки, якщо знехтувати силами тертя. Сила, яка діє на кульку масою m є рівнодійною двох сил: сили тяжіння
рух такого маятника є прикладом гармонічного коливного руху матеріальної точки, якщо знехтувати силами тертя. Сила, яка діє на кульку масою m є рівнодійною двох сил: сили тяжіння  і сили натягу нитки
і сили натягу нитки  . Рівнодійна сила
. Рівнодійна сила  , яка діє вздовж дуги, за величиною рівна
, яка діє вздовж дуги, за величиною рівна  і в разі малих кутів
і в разі малих кутів  буде дорівнювати:
буде дорівнювати:  . Тоді рівняння руху кульки запишеться:
. Тоді рівняння руху кульки запишеться: .
.
 :
: , або
, або  .
.
 , що є розв’язком диференціального рівняння (1.2.2), змінюється в часі за законом:
, що є розв’язком диференціального рівняння (1.2.2), змінюється в часі за законом: ,
, ,
, ,
, де
де  ,
,  і
і  ,
,  . Величина А дорівнює найбільшому абсолютному значенню фізичної величини
. Величина А дорівнює найбільшому абсолютному значенню фізичної величини  визначає значення
визначає значення 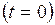 фаза дорівнює початковій фазі
фаза дорівнює початковій фазі  , (1.2.3)
, (1.2.3) –довжина маятника.
–довжина маятника. і
і  одержуємо:
одержуємо: .
.
 достатньо виміряти різницю довжин
достатньо виміряти різницю довжин 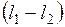 , не вимірюючи
, не вимірюючи 


