
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Короткі відомості про вимірювання фізичних величин та похибки 8Содержание книги
Поиск на нашем сайте
ЛАБОРАТОРНИЙ ФІЗИЧНИЙ ПРАКТИКУМ
Рекомендовано Міністерством освіти і науки України як навчальний посібник для студентів вищих навчальних закладів
Чернівці “Рута”
ББК 22.3я7 Д 279 УДК 53(076.5)
Рекомендовано Міністерством освіти і науки України як навчальний посібник для студентів вищих навчальних закладів (Лист №1.4/18 – Г-1623 від 7.07.2008 р.)
Рецензенти: Кідалов В. В., доктор фізико-математичних наук, професор, завідувач кафедри фізики Бердянського державного педагогічного університету; Шайко-Шайковський О. Г., доктор технічних наук, професор кафедри загальної фізики Чернівецького національного університету імені Юрія Федьковича; Дідора Т.Д., кандидат фізико-математичних наук, доцент, завідувач кафедри фізики і методики її викладання Тернопільського національного педагогічного університету імені В. Гнатюка.
Д 279 Дейбук В. Г., Кшевецький О. С. Лабораторний фізичний практикум: Навчальний посібник. – Чернівці: Рута, 2008. – 210 с.
ISBN 978–966–568–992–8
У посібнику наведено лабораторні роботи з основних розділів фізики. До першої частини увійшли двадцять вісім стендових робіт. Друга частина містить тринадцять віртуальних (комп’ютерних) лабораторних робіт. До кожної роботи подано контрольні запитання, а віртуальні роботи включають також тестові запитання для допуску до виконання практикуму. Для викладачів та студентів вищих навчальних закладів, що вивчають курс фізики. Може бути також використаний студентами середніх технічних навчальних закладів. ББК 22.3я7 УДК 53(076.5) ISBN 978–966–568–992–8
© “Рута”, 2008 © Дейбук В.Г., Кшевецький О.С., 2008
ЗМІСТ
Передмова 7 Короткі відомості про вимірювання фізичних величин та похибки 8
І. СТЕНДОВІ ЛАБОРАТОРНІ РОБОТИ
Фізичні основи механіки. Механічні коливання
Молекулярна фізика та термодинаміка
Електрика та магнетизм
Оптика
Ядерна фізика
ІІ. ВІРТУАЛЬНІ ЛАБОРАТОРНІ РОБОТИ
Вказівки щодо виконання комп’ютерних лабораторних робіт 116
Фізичні основи механіки. Механічні коливання
Електрика та магнетизм
Додаток 197 Рекомендована література 209 ПЕРЕДМОВА
Фізика – фундаментальна дисципліна, яка закладає наукове підґрунтя для вивчення всіх інженерно-технічних дисциплін, оволодіння нею сприяє розвитку мислення, формуванню світогляду студентів на основі сучасних досягнень науки і техніки, глибокому розумінню явищ і процесів у навколишньому середовищі. Знання теоретичного матеріалу фізики є не достатньо повними без уміння застосувати фізичні закони на практиці. Лабораторні роботи дають можливість зрозуміти і запам’ятати основні закони і формули фізики, а також особливості і межі їх застосування. На лабораторних заняттях студенти поглиблюють знання, які вони отримали на лекціях та практичних заняттях, ознайомлюються з деякими основними приладами, оволодівають різними методами вимірювань і технікою експерименту. Останнім часом значно зросла роль і розширились можливості застосування нових інформаційних технологій під час вивчення курсу фізики, внаслідок чого зовсім по-новому стали будуватися практичні і лабораторні заняття. Саме тому автори поряд з класичними лабораторними роботами включили й віртуальні (комп’ютерні) роботи, які виконуються на базі спеціально розробленого програмного забезпечення. В основу посібника покладені лабораторні роботи, які впродовж останніх років пропонувалися студентам спеціальностей «Харчові технології та інженерія», «Товарознавство і торговельне підприємництво» Чернівецького торговельно-економічного інституту Київського національного торговельно-економічного університету під час проведення лабораторного фізичного практикуму. Книжка складається з двох частин. До першої увійшли двадцять вісім стендових лабораторних робіт, які виконуються безпосередньо у фізичній лабораторії. Друга частина – це тринадцять віртуальних лабораторних робіт, виконання яких пов’язане з використанням комп’ютерного моделювання фізичних процесів. Ці лабораторні роботи виконуються в комп’ютерному класі. До кожної лабораторної роботи сформульовано мету, подано короткі теоретичні відомості з описом будови приладів і установок, вказано послідовність виконання і описано методику обробки експериментальних даних. Наведено контрольні запитання та список рекомендованої літератури. Виконанню кожної лабораторної роботи має передувати значна самостійна підготовка студентів (вивчення відповідного теоретичного матеріалу, знайомство з описом роботи тощо). Пропонований посібник буде корисним студентам також і для набуття навичок в організації самостійної роботи. Автори висловлюють вдячність рецензентам за зауваження та рекомендації, кандидату фізико-математичних наук, доценту О.О. Боднарук за корисні поради під час підготовки рукопису, а також старшому лаборанту Л.В.Ворошиловій за вагому допомогу у підготовці рукопису до видання. КОРОТКІ ВІДОМОСТІ СТЕНДОВІ ЛАБОРАТОРНІ РОБОТИ
ФІЗИЧНІ ОСНОВИ МЕХАНІКИ. МЕХАНІЧНІ КОЛИВАННЯ
ЛАБОРАТОРНА РОБОТА №1.1 ТЕОРЕТИЧНІ ВІДОМОСТІ Для вимірювання лінійних та кутових величин користуються різноманітними приладами та інструментами. Найпростіші з них: штангенциркуль, мікрометр, мікроскоп, кутомір та ін. Довжини вимірюють масштабними лінійками, рулетками. Величина найменшої поділки такої лінійки зветься ціною однієї поділки. Зазвичай ціна однієї поділки лінійки рівна 1 мм. Перша риска вважається нулем (нульова риска). Якщо вимірювання проводять з точністю до долі міліметра, то користуються допоміжною шкалою вимірювального інструмента – ноніусом. Ноніус буває лінійний – для вимірювання лінійних величин, та кутовий – для вимірювання кутових величин. Штангенциркуль Лінійний ноніус є невеликою лінійкою С зі шкалою, m поділок якої дорівнюють m – 1 поділкам шкали масштабної лінійки А. Ноніус С можна переміщувати по лінійці А (рис. 1.1.1).
Отримана з формули (1.1.1) різниця  називається точністю ноніуса, тобто точність ноніуса називається точністю ноніуса, тобто точність ноніуса  рівна відношенню ціни найменшої поділки масштабної лінійки до кількості поділок на ноніусі. Точність ноніуса часто буває 1/10 мм або 1/20 мм. рівна відношенню ціни найменшої поділки масштабної лінійки до кількості поділок на ноніусі. Точність ноніуса часто буває 1/10 мм або 1/20 мм.
Виміри за допомогою ноніуса виконують так: до нульової риски шкали лінійки прикладають один кінець вимірюваного тіла В, до другого кінця – ноніус С (рис. 1.1.2) З рис. 1.1.2 бачимо, що шукана довжина тіла В (заштрихованого на рис. 1.1.2)
де k – ціле число поділок масштабної лінійки в мм, яке вкладається у вимірювану довжину; Визначаємо, які поділки ноніуса та лінійки збігаються. Позначаємо n той номер поділки ноніуса, який збігається з певною поділкою масштабної лінійки, тоді
З формули (1.1.2) і (1.1.3) знаходимо шукану довжину
Якщо припустити
Отже, довжина вимірюваного тіла рівна цілому числу k мм масштабної лінійки плюс n десятих часток мм. З рис. 1.1.2 видно, що:
Штангенциркуль (рис. 1.1.3) складається зі сталевої міліметрової лінійки А, з одного кінця якої є нерухома ніжка В. Друга ніжка D має ноніус С і може переміщатись вздовж лінійки А. Коли ніжки В і D стискаються, нуль лінійки і нуль ноніуса мають збігатися. Для того, щоб виміряти довжину предмета М, його розміщують між ніжками, які торкаються предмета М (без сильного натиску), і закріплюють положення рухомої ніжки гвинтом Е. Після цього знімають покази на лінійці і ноніусі та розраховують розміри предмета М за формулою (1.1.4). Мікрометр Мікрометричний гвинт використовується у вимірювальних приладах вищої точності (мікрометр, мікроскоп) і дає можливість визначати розміри тіл до сотої частки міліметра. Мікрометричний гвинт являє собою стрижень, який має точну гвинтову нарізку. Висота підйому гвинтової нарізки за один оберт називається кроком мікрометричного гвинта.
Для того, щоб мікрометричний гвинт А перемістився на 1 мм, необхідно зробити два оберти барабана С. Таким чином, крок мікрометричного гвинта дорівнює 0,5 мм. У мікрометрі на барабані С є шкала, яка має 50 поділок. Якщо крок гвинта
Для вимірювання мікрометром предмет поміщають між упором Е і мікрометричним гвинтом А (рис. 1.1.4) і обертають гвинт А за головку М до тих пір, поки вимірюваний предмет не буде затиснутий між упором Е і кінцем гвинта А (гвинт А обертають тільки за головку М, тому що в іншому випадку легко збити збіг нулів шкали стебла D і барабана С). Довжину
де На рис. 1.1.5 маємо
ПОРЯДОК ВИКОНАННЯ РОБОТИ Обробка результатів вимірів Штангенциркулем вимірюють висоту h і діаметр d циліндра. Виміри проводять так: 1. Циліндр розміщують між ніжками B і D штангенциркуля (легко торкаючись його) і закріплюють гвинт рухомої ніжки гвинтом Е. 2. Вимірюють довжину і діаметр циліндра, проводячи за шкалою лінійки А відлік кількості цілих міліметрів k, розташованих зліва від нульової поділки ноніуса і кількості поділок n шкали ноніуса. За формулою (1.1.4) роблять підрахунки. Виміри проводять три рази, трохи прокручуючи циліндр між ніжками. 3. Розраховують абсолютну і відносну похибки вимірювань. Результати вимірювань та розрахунків заносять у таблиці 1.1.1 і 1.1.2. Таблиця 1.1.1
Таблиця 1.1.2
Вимірювання мікрометром і Обробка результатів вимірів
1. Предмет, який потрібно виміряти (товстий дріт або металева пластинка), поміщають між упором Е і кінцем мікрометричного гвинта А. 2. Знаходять значення k і n на шкалі стебла D і барабана С. За формулою (1.1.6) підраховують шукану величину. 3. Виміри діаметра дроту 4. Обчислюють абсолютну і відносну похибки вимірів. Результати вимірювань та обчислень заносять у таблиці 1.1.3 і 1.1.4. Таблиця 1.1.3
Таблиця 1.1.4
КОНТРОЛЬНІ ЗАПИТАННЯ 1. Для чого використовується ноніус? Які бувають ноніуси? 2. Ціна поділки ноніуса штангенциркуля, мікрометра. 3. Пояснити методику вимірювань. 4. Що значить абсолютна і відносна похибки? Яка різниця між ними? 5. Дійсне значення вимірюваної величини. Як воно записується? ЛАБОРАТОРНА РОБОТА № 1.2
ТЕОРЕТИЧНІ ВІДОМОСТІ
Коливаннями або коливальними рухами називаються рухи або зміни стану, що повторюються з часом. Коливання бувають різними за своєю фізичною природою: механічні коливання тіла, підвішеного на пружині (пружинний маятник); гойдання маятників; коливання струн; вібрація фундаментів конструкцій; електромагнітні коливання тощо. Коливання називаються періодичними, якщо значення фізичних величин, які змінюються в процесі коливань, повторюються через рівний проміжок часу. Періодом коливань Частотою періодичних коливань
Циклічною (круговою) частотою періодичних коливань називається число повних коливань, що здійснюються за
Математичний маятник – це прилад, що складається з металевої кулі, яка підвішена на тонкій довгій нерозтяжній нитці (масою нитки можна знехтувати). Для невеликих кутів відхилення
Перед силою F стоїть мінус, оскільки вона напрямлена проти додатного напрямку координати зміщення x. Рівняння (1.2.1) можна записати, якщо
На рис. 1.2.1 показано напрямки цих сил. Періодичні коливання – це гармонічні коливання, у яких фізична величина
де тоді
Період коливань математичного маятника у цьому випадку визначається:
де Досліди для визначення прискорення вільного падіння проводять для різних довжин маятника. Для двох різних довжин маятника
Отже, для визначення прискорення
МЕТОДИКА ВИМІРЮВАНЬ
На рис. 1.2.1 показано математичний маятник. Ниткою задають певну довжину Із закону всесвітнього тяжіння Ньютона
ПОРЯДОК ВИКОНАННЯ РОБОТИ
1. Виміряти довжину математичного маятника 2. Для знайденої довжини визначити час 20 – 100 повних коливань і підрахувати період коливань 3. Змінити довжину маятника, визначити період. Вимірювання повторити не менше 3-х разів. 4. Обчислити прискорення земного тяжіння g за формулою (1.2.4). 5. Визначити масу та густину Землі (1.2.5). 6. Розрахувати абсолютні та відносні похибки визначення
7. Всі обчислені і виміряні величини занести в таблицю 1.2.1:
Таблиця 1.2.1
КОНТРОЛЬНІ ЗАПИТАННЯ 1. Що таке прискорення і сила? 2. Сформулювати ІІ-й закон Ньютона. 3. Сформулювати закон всесвітнього тяжіння. 4. Вивести рівняння гармонічного коливного руху математичного маятника. 5. Дати визначення параметрів коливного руху: амплітуди, фази, частоти, періоду. 6. Як залежить прискорення вільного падіння від географічної широти? ЛАБОРАТОРНА РОБОТА №1.3 ТЕОРЕТИЧНІ ВІДОМОСТІ
Основний закон динаміки обертального руху твердого тіла, для якого
де Момент сили відносно нерухомої осі чисельно дорівнює добутку сили на її плече, тобто найкоротшу відстань від осі обертання до лінії дії сили. Момент інерції тіла відносно будь-якої осі дорівнює сумі моментів інерції всіх матеріальних точок тіла відносно цієї осі
де
МЕТОДИКА ВИМІРЮВАНЬ
Запишемо рівняння поступального руху маховика в проекції на вертикальну вісь:
де Р – сила тяжіння маятника; Т – сила натягу нитки; m – маса маятника; а – прискорення центра тяжіння валика. Рівняння обертального руху маятника запишеться
де J – момент інерції маятника, Прискорення центра мас пов’язане з кутовою швидкістю співвідношенням
Розв’язавши рівняння (1.3.1), (1.3.2), (1.3.3) відносно прискорення центра мас, знаходимо:
Прискорення а можна також визначити з рівняння рівноприскореного поступального руху маятника:
де S – шлях, що пройшов центр мас маятника із верхнього крайнього положення в нижнє; t – час одного повного розкручування маятника. Відомо, що величина прискорення і сили тяжіння не залежать від напрямку руху маятника (вгору чи вниз). Під час коливань маятника швидкість змінює свій знак, а прискорення не змінює, як і рівнодійна сила.
ПОРЯДОК ВИКОНАННЯ РОБОТИ 1. Зважити маятник (валик і диск) m. 2. Визначити масу валика за формулою | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |





 .
.

 ,
,
 – відрізок довжини, який є часткою міліметра.
– відрізок довжини, який є часткою міліметра. .
.
 .
.
 мм,
мм,  поділок, то шукана довжина
поділок, то шукана довжина мм.
мм.
 мм
мм  мм, оскільки
мм, оскільки  мм,
мм,  .
.
 Мікрометр (рис. 1.1.4 і 1.1.5) складається з двох основних частин: скоби В і мікрометричного гвинта А. Мікрометричний гвинт А проходить крізь отвір скоби В з внутрішньою різьбою. Напроти мікрометричного гвинта, на скобі, є упор Е. На мікрометричному гвинті закріплений порожнистий циліндр (барабан) С з поділками по колу. Під час обертання мікрометричного гвинта барабан ковзає по лінійній шкалі, нанесеній на стеблі D.
Мікрометр (рис. 1.1.4 і 1.1.5) складається з двох основних частин: скоби В і мікрометричного гвинта А. Мікрометричний гвинт А проходить крізь отвір скоби В з внутрішньою різьбою. Напроти мікрометричного гвинта, на скобі, є упор Е. На мікрометричному гвинті закріплений порожнистий циліндр (барабан) С з поділками по колу. Під час обертання мікрометричного гвинта барабан ковзає по лінійній шкалі, нанесеній на стеблі D. Найбільш розповсюджений мікрометр з ціною поділки лінійної шкали стебла
Найбільш розповсюджений мікрометр з ціною поділки лінійної шкали стебла  мм. Верхні і нижні риски шкали зсунуті одна відносно одної на половину міліметра; цифри проставлені тільки для поділок нижньої шкали (рис. 1.1.5).
мм. Верхні і нижні риски шкали зсунуті одна відносно одної на половину міліметра; цифри проставлені тільки для поділок нижньої шкали (рис. 1.1.5). мм, а число поділок барабана
мм, а число поділок барабана  , то точність мікрометра складає:
, то точність мікрометра складає:
 предмета знаходять за формулою
предмета знаходять за формулою ,
,
 – число найменших поділок шкали,
– число найменших поділок шкали,  – ціна найменшої поділки шкали,
– ціна найменшої поділки шкали,  – число всіх поділок на шкалі барабана,
– число всіх поділок на шкалі барабана,  – номер поділки барабана, яка в момент відліку збіглася з віссю шкали стебла D.
– номер поділки барабана, яка в момент відліку збіглася з віссю шкали стебла D. мм
мм  мм
мм  мм.
мм. , мм
, мм

 , мм
, мм






 Середнє
значення
Середнє
значення


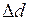 , мм
, мм

 , мм
, мм




 Середнє
значення
Середнє
значення



 повторюють не менше трьох разів у різних місцях.
повторюють не менше трьох разів у різних місцях.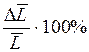
 , мм
, мм





 Середнє
значення
Середнє
значення


 h, мм
h, мм





 Середнє
значення
Середнє
значення


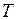 називається той найменший проміжок часу, через який повторюються значення всіх величин, які характеризують коливальні рухи. За цей час здійснюється одне повне коливання.
називається той найменший проміжок часу, через який повторюються значення всіх величин, які характеризують коливальні рухи. За цей час здійснюється одне повне коливання. називається число повних коливань, які здійснюються за одиницю часу:
називається число повних коливань, які здійснюються за одиницю часу:
 одиниць часу:
одиниць часу: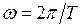 , тоді
, тоді  .
. рух такого маятника є прикладом гармонічного коливного руху матеріальної точки, якщо знехтувати силами тертя. Сила, яка діє на кульку масою m є рівнодійною двох сил: сили тяжіння
рух такого маятника є прикладом гармонічного коливного руху матеріальної точки, якщо знехтувати силами тертя. Сила, яка діє на кульку масою m є рівнодійною двох сил: сили тяжіння  і сили натягу нитки
і сили натягу нитки  . Рівнодійна сила
. Рівнодійна сила  , яка діє вздовж дуги, за величиною рівна
, яка діє вздовж дуги, за величиною рівна  і в разі малих кутів
і в разі малих кутів  буде дорівнювати:
буде дорівнювати:  . Тоді рівняння руху кульки запишеться:
. Тоді рівняння руху кульки запишеться: .
.
 :
: , або
, або  .
.
 , що є розв’язком диференціального рівняння (1.2.2), змінюється в часі за законом:
, що є розв’язком диференціального рівняння (1.2.2), змінюється в часі за законом: ,
, ,
, ,
, де
де  ,
,  і
і  ,
,  . Величина А дорівнює найбільшому абсолютному значенню фізичної величини
. Величина А дорівнює найбільшому абсолютному значенню фізичної величини  визначає значення
визначає значення 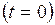 фаза дорівнює початковій фазі
фаза дорівнює початковій фазі  , (1.2.3)
, (1.2.3) –довжина маятника.
–довжина маятника. і
і  одержуємо:
одержуємо: .
.
 достатньо виміряти різницю довжин
достатньо виміряти різницю довжин 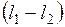 , не вимірюючи
, не вимірюючи  , заміряють час t, за який здійснюється 20 – 100 коливань, визначають час одного коливання – період
, заміряють час t, за який здійснюється 20 – 100 коливань, визначають час одного коливання – період  . Такі ж виміри повторюють для другої довжини
. Такі ж виміри повторюють для другої довжини  , де
, де  – маса Землі,
– маса Землі,  – радіус Землі в даному місці (прийняти
– радіус Землі в даному місці (прийняти  км), G – гравітаційна стала
км), G – гравітаційна стала  обчислюють масу Землі. За підрахованою масою і знайденим об’ємом Землі визначають густину Землі
обчислюють масу Землі. За підрахованою масою і знайденим об’ємом Землі визначають густину Землі  .
. ;
; 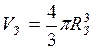 ;
;  . (1.2.5)
. (1.2.5) .
. ;
;  .
.

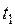 , с
, с
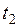 , с
, с
 , с
, с
 , с
, с


 , запишеться
, запишеться ,
, – сума моментів усіх сил, які діють на систему; J – момент інерції тіла;
– сума моментів усіх сил, які діють на систему; J – момент інерції тіла;  – кутове прискорення,
– кутове прискорення,  – кут повороту,
– кут повороту,  – час повороту.
– час повороту.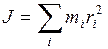 ,
,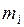 – маса і -тої матеріальної точки,
– маса і -тої матеріальної точки,  – відстань від і -тої матеріальної точки до осі обертання.
– відстань від і -тої матеріальної точки до осі обертання.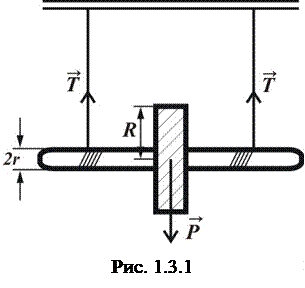 Невеликий диск (маховичок), насаджений на вісь, опускається під дією сили тяжіння на двох нитках, які розмотуються на всю довжину. Маховик продовжує обертальний рух у зворотному напрямку, в результаті чого сам підіймається вгору, і при цьому гальмує свій рух. Дійшовши до верхньої точки, диск знову опускатиметься вниз і т.д. Маховик здійснюватиме коливання вгору і вниз, тому він і називається маятником. На рис. 1.3.1 зображений маятник Максвелла.
Невеликий диск (маховичок), насаджений на вісь, опускається під дією сили тяжіння на двох нитках, які розмотуються на всю довжину. Маховик продовжує обертальний рух у зворотному напрямку, в результаті чого сам підіймається вгору, і при цьому гальмує свій рух. Дійшовши до верхньої точки, диск знову опускатиметься вниз і т.д. Маховик здійснюватиме коливання вгору і вниз, тому він і називається маятником. На рис. 1.3.1 зображений маятник Максвелла. ,
,
 ,
,
 – кутове прискорення,
– кутове прискорення,  , а момент інерції диска має вигляд:
, а момент інерції диска має вигляд:  , де
, де  – маса валика,
– маса валика,  – маса диска, R – радіус диска.
– маса диска, R – радіус диска. .
.
 .
.
 ,
,
 , де V – об’єм валика;
, де V – об’єм валика; 


