
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кореляційне відношення ПірсонаСодержание книги Поиск на нашем сайте Для вимірювання тісноти зв’язку між двома явищами використовується кореляційне відношення Процедури обчислень кореляційного відношення та індекса кореляції дуже схожі. Відмінність полягає в тому, що при обчисленні кореляційного відношення виходять із частинних середніх, а не з відповідних значень регресії. Кореляційне відношення Пірсона
gj – частота j- ї групи (інтервала) значень змінної х, j=1,2,…,t.
уkj - k -те значення залежної змінної у в j -й групі (інтервалі) значень пояснювальної змінної х, k=1,2,…,5. Якщо числовий матеріал поданий у вигляді кореляційної таблиці, то на практиці зручно користуватись формулою:
. Частіше всього кореляційне відношення тим більше, чим більш дифиренційоване групування по залежній змінній. Оскільки при обчисленні виходять із середніх, тому очевидно, що 4. Коефіцієнт конкордації. В економіці існує велике число явищ, ознаки яких не піддаються точній кількісній оцінці. Це так звані атрибутні ознаки. Наприклад, професія, форма власності, якість виробу, техноолгічні операції і так далі. Дослідник ранжирує елементи сукупності, приписуючи кожному з них порядковий номер, що відповідає підсумкам порівнянь по даній ознаці з іншими елементами. Якщо кількість ознак- змінних більше двох, то в результаті ранжировок п елементів (підприємств чи установ) мають справу з т послідовностями рангів. Для перевірки, чи добре узгоджуються ці т ранжировок одна з одною, використовують коефіцієнт конкордації Кендела:
При наявності зв’язних (об’єднаних рангів) коефіцієнт конкордації W обчислюється за формулою:
де j – сума рангів, приписаних всіми експертами і -му елементу вибірки, мінус середнє значення цих сум рангів; т – число експертів чи ознак, зв’язок між якими оцінюється; п - об’єм вибірки (кількість підприємств чи установ), іншими словами, це кількість членів послідовності рангів;
Коефіцієнт W приймає значення: Тема: „Регресійний аналіз”. Поняття регресії. Регресія – це одностороння стохастична залежність. Вона встановлює відповідність між випадковими змінними. Одностороння стохастична залежність виражається за допомогою функції, яка, для відмінності її від строго математичної функції, називається функцією регресії або просто регресією. видирегресії: I. Відносно числа явищ (змінних), що враховуються в регресії, розрізняють: · просту регресію (між двома змінними); · множинну чи частинну регресію (між залежною змінної у і декількома (пояснювальними) незалежними змінними х1,х2,...,хm). II. Відносно форми залежності розрізняють: · лінійну регресію, що виражається лінійною функцією; · нелінійну регресію, виражається нелінійною функцією. III. В залежності від характеру регресії розрізняють: · додатну регресію (якщо із збільшенням чи зменшенням значень пояснювальної змінної значення залежної змінної також відносно від’ємну регресію збільшуються чи зменшуються). IV. Відносно типу з’єднань явищ розрізняють: · безпосередню регресію (явища з’єднані безпосередньо між собою); · опосередковану регресію (пояснювальна змінна діє на результативну змінну через деяку третю або через ряд інших змінних); · нонсенс-регресію (хибна або абсурдна регресія). 1. Регресійнийаналіз – сукупність статистичних методів, що орієнтовані на дослідження стохастичної залежності однієї змінної Y від набору інших змінних Його основними задачами є: 1) Встановлення форми залежності Y від Додатна регресія:
а) лінійна б) рівноприскорено в) рівносповільнено зростаюча зростаюча Від’ємна регресія:
г) лінійна д) рівноприскорено є) рівносповільнено спадаюча спадаюча 2) Визначення функції регресії (у вигляді математичного рівняння того чи іншого типу). 3) Оцінка невідомих значень залежної змінної. З допомогою функції регресії можна відтворити значення залежної змінної всередині інтервалу заданих значень пояснювальних змінних (тобто розв’язати задачу (інтерполяції) чи оцінити хід процесу за межами заданого інтервалу (тобто розв’язати задачу екстраполяції)). Ці задачі розв’язуються шляхом підстановки у відповідне рівняння регресії значень пояснювальних змінних. Результатом є оцінка значення залежної змінної. 2. Нехай позначимо залежну змінну через у, а пояснювальні змінні через
кількісно оцінюється усереднена залежність між досліджуваними змінними. Випадкова змінна U характеризує відхилення
змінної у від середньої величини у, обчисленої за формулою (1). Змінна U називається збуренням (возмущением). Вона включає вплив неврахованих факторів змінних, випадкових похибок і помилок спостережень. Таким чином, значення у можна представити у вигляді:
або з врахуванням (1):
3.1. Діаграма розсіювання При аналізі залежності між двома змінними застосовують діаграму розсіювання, яка є наглядною формою представлення інформації. За шириною розкидання точок можна зробити висновок про степінь тісноти зв’язку. Якщо точки розміщенні близько один до одної у вигляді вузької полоски, то можна стверджувати про наявність відносно тісного зв’язку. Якщо точки розкидані широко по діагоналі, то маємо слабкий зв’язок. Переваги: простота побудови. Недоліки – неточність і можливість застосувати лише для залежності двох змінних, для трьох змінних можлива, хоч і важче, а при великій кількості змінних геометрично представити неможливо. 3.2. Метод частинних середніх Середнє, зв’язане з деякими припущеннями чи обчислена при визначених умовах, називається частинним умовним чи груповим середнім. Частинні середні змінних х та у, обчислюються за формулами:
Якщо одному значенню хі відповідає тільки одне значення yi, то останнє також є частинним середнім. Якщо одному значенню хі відповідає декілька значень yi, то частинне середнє обчислюється по цьому ряду значень. Таким чином, частинні середні вирівнюють різні значення yi, що відповідають одному значенню хі. Аналогічно отримають частинні середні змінної х.
Під простоюрегресією ми розуміємо односторонню стохастичну залежність результативної змінної тільки від однієї пояснювальної змінної:
Оскільки передбачається лінійний характер залежності усереднених значень результат змінної
Невідомі параметри регресії Стала перетину прямої регресії з віссю ординат. Коефіцієнт
1. Метод найменших квадратів Графічно цю задачу можна представити так – у полі розсіювання (xi, yi) площини хоу необхідно провести пряму так, щоб величина всіх відхилень відповідна умові:
Тому цей метод регресійного аналізу називається методом найменших квадратів (МНК). Для знаходження коефіцієнтів залежності (8), необхідно знайти часткові похідні по b0 та b1 від функції (9) і прирівняти їх до нуля
Після простих перетворень отримаємо систему нормальних рівнянь:
(11)
Визначивши b0 та b1, можна по (8) обчислити значення регресії для заданої області пояснювальної змінної х. Зауваження. На практиці коефіцієнти b0 та b1 частіше знаходять з використанням коефіцієнтів кореляції та коваріації. (1.2.) Алгоритм ручного рахунку: 1) знаходимо середні значення масивів Х та У:
2) знаходимо вибіркові відхилення:
3) знаходимо коефіцієнт коваріації:
4) знаходимо коефіцієнт кореляції:
5) знаходимо коефіцієнт рівняння регресії:
6) знаходимо теоретичні значення змінної У:
7) знаходимо середнє відхилення, смугу відхилення та інтервал довір’я:
(1.3.) Лінеаризації у випадку криволінійних залежностей На практиці дуже часто зв’язок між двома параметрами носить нелінійний(криволінійний) характер. У більшості випадків за допомогою простих перетворень можна нелінійну залежність до лінійної, тобто провести лінеаризацію. (1.4 .) Визначення параметрів парної лінійної регресії для згрупованих даних Для кореляційної таблиці, яку розглянули раніше, мають місце наступні співвідношення:
Середні значення
Шляхом заміни в (12) і (13) окремих значень хі та уі серединами інтервалів, що зважені за відповідними частотами, отримаємо формули для обчислення оцінок параметрів за згрупованими дуними:
Множинна лінійна регресія При існуванні лінійного співвідношення між змінними, загальний вираз рівняння множинної регресії (1) записується у вигляді:
Підставляючи (34) в (30) маємо:
або (35)
З системи нормальних рівняннь отримуємо b0 та b1:
Загальна процедура проведення регресійного аналізу включає в себе наступні етапи: 1. Формулювання економічної проблеми. На даному етапі формулюються гіпотези про залежність економічних явищ. Потім залежність кількісно оцінюється за допомогою методів регресійного аналізу, а саме яку форму і який вид може дана залежність. 2. Ідентифікація змінних. Визначають найбільш оптимальну кількість змінних, і класифікують їх на залежні і пояснювальні змінні. 3. Збір статичних даних. Приймається рішення про проведення досліджень за всією генеральною сукупністю чи за її вибіркою. Після цього приступають до збору даних для кожної змінної, включеної в аналіз. 4. Специфікація функції регресії. На цьому етапі дослідження, висувається конкретна гіпотеза про форму зв’язку. 5. Оцінка функції регресії. Визначаються числові значення параметрів регресії. Крім того, обчислюється ряд статичних показників, що характеризують точність регресійного аналізу. 6. Оцінка точності регресійного аналізу. На цьому етапі повинні бути зроблені висновки про точність результатів. 7. Економічна інтерпретація. Результати регресійного аналізу порівнюються з гіпотезами, що були сформульовані на першому етапі дослідження, і оцінюється їх правдоподібність з економічної точки зору. 8. Передбачення невідомих значень залежної змінної(прогноз). Прогноз отримують шляхом підстановки в регресій не рівняння, з чисельно оціненими параметрами, значень пояснювальної змінної.
|
||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 787; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 запропоноване Пірсоном.
запропоноване Пірсоном.
 (8)
(8) - частинне середнє змінної у для j -ї групи (інтервала) значень пояснювальної змінної х;
- частинне середнє змінної у для j -ї групи (інтервала) значень пояснювальної змінної х;
 (9)
(9)
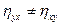 .
. (10)
(10) ,
,  (11)
(11) (12)
(12) , Вk – число зв’язаних рангів, k=1,…,z.
, Вk – число зв’язаних рангів, k=1,…,z. .
. .
. ;
;

 . Таким чином, змінна у є функцією від змінної хк. Оскільки випадкові і другорядні фактори не можуть бути виключені із експериментальних даних, залежність набуває стохастичний характер. З допомогою функції регресії
. Таким чином, змінна у є функцією від змінної хк. Оскільки випадкові і другорядні фактори не можуть бути виключені із експериментальних даних, залежність набуває стохастичний характер. З допомогою функції регресії (1)
(1) (2)
(2) (3)
(3) (4)
(4)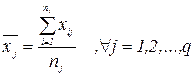 (5)
(5) (6)
(6) (7)
(7) , то цю залежність виражають за допомогою функції лінійної регресії. Формула (7) набуде вигляду:
, то цю залежність виражають за допомогою функції лінійної регресії. Формула (7) набуде вигляду:
 (8)
(8) і
і  підлягають оцінці за визначеною процедурою. Далі будемо називати їх оцінкою параметрів.
підлягають оцінці за визначеною процедурою. Далі будемо називати їх оцінкою параметрів. значення 1(фіктивна змінна, як правило, не записується, але іноді з якоїсь точки зору її зручно виявити в рівняння).
значення 1(фіктивна змінна, як правило, не записується, але іноді з якоїсь точки зору її зручно виявити в рівняння). . Згідно рівняння (8)
. Згідно рівняння (8)  на одну одиницю. Знак
на одну одиницю. Знак 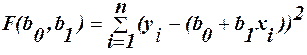 (9)
(9)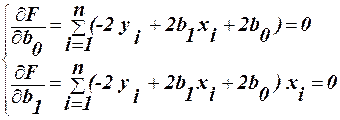 (10)
(10)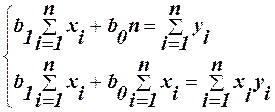
 (12)
(12) (13)
(13) ,
,  (14)
(14) ,
, 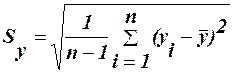 (15)
(15)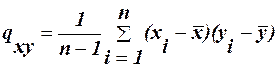 (16)
(16)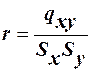 (17)
(17)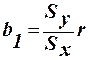
 (18)
(18)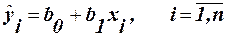 (19)
(19) (20)
(20) - смуга;
- смуга;  (21)
(21)
 (23)
(23)
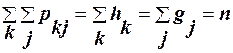 (24)
(24)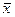 та
та  визначаються, як середні зважені за серединами інтервалів:
визначаються, як середні зважені за серединами інтервалів: (25)
(25) (26)
(26)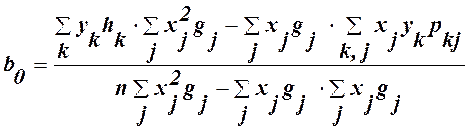 (27)
(27)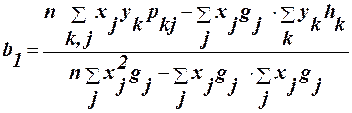
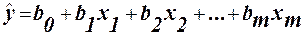 (29)
(29)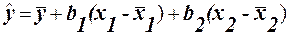
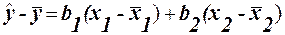
 (36)
(36) (37)
(37)


