
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття класифікації, задача класифікаціїСодержание книги
Поиск на нашем сайте
Під терміном класифікація розум розподіл предметів за заг. класами згідно най б. суттєвих ознак, які притаманні предметам даного типу і які відрізняють їх від предметів інших типів. Класиф провод за наступними правилами: 1. в одній класиф. викор. Одна основа; 2. об’єм класу = сумі об’ємів підкласів коли і підкласи пересікаються; 3. поділ на підкласи пр неперервно. Виявлення природного розподілу вихідних спостережень і розбиття на чіткі групи: кластери, таксони. Типізація – сукупність даних і об’єктів розбив. на порівняно велику областей групув. так щоб елементи однієї області знах. один від одного на невеликій відстані; в кластері дані про близькість. Класиф. об’єктів можна пров. за допомогою якісних, кількісних і інших ознак. Викор-ся формальні мат. Методи розбиття на класи є експериментальним метод, при якому розб. на класи проводять спеціалісти з однієї області, використовуючи проф. знання, доск. Кластерний аналіз – це сукупність методів, але розбиття спостер. на однорідні групи. Техніка класиф. викор. в різних областях. Задачі класт. аналізу є 2-х видів: за об’ємом – класиф. відносно невеликих за об’ємом сукупностей; класиф. великих об’ємів багатовимірних спостережень. Задачі класиф. ділять за типом апріорної інф-ції: 1. кількість класів задана; 2. кількість класів невідана і її треба визнач.; 3. кількість класів непотрібна. Дерева – агломеративне та дивизивне Основні поняття кластерного аналізу; застосування Виділяють 3 основні кластерні процедури: 1. ієрархія алгоритмів ідомезивні; 2. паралельна процедура за допомогою ітераційних алгоритмів; 3. послідовні процедури з малою кількістю спостережень. Кластер – накопичення, група елементів, які хар-ся деякою заг. властивістю, методи їх знаходження і є кластер ний аналіз. Таксон – систематизована група б-я категорії, методи їх знаходження назив. чисельною таксономією. Матричний простір – пара (х,d), яка склад-ся з деякої множини елементів простору Хі і відстані d. Функція відстані – однозначна, невідємна, дійсна ф-ція для якої викон-ся аксіоми: 1. d(xu, xs)≥0; 2. d(xu, xs)=0 – максимальна близькість елементів з самим собою, коли xu=xs; 3. d(xu, xs)= d(xs, xu,) – симетрія; 4. d(xu, xs)≤ d(xu, xz)+ d(xz, xs). Міра подібності - однозначна, невідємна, дійсна ф-я Г(xu, xs), яка визначена для б-я xs, якщо виконується аксіома: а). 0≤ r(xu, xs)<1, б-я Типи відстаней і мір подібностей В ієрархічних схемах групування об’єктів найбільш розповсюдженою формою графічного зображення є дендограма і її двовимірним аналогом дендограф. Одновимірний граф для зображення із заданої множини. Об’єкти розміщені за ієрархічними рівнями так щоб підкреслити їх взаємну подібність на основі вимірювань. 0бєднання елементів групи має зміст в умовах високого ступеня подібності між ними. Компактне групування свідчить про силу зв’язків між об’єктами, компоненти на слабку залежність. Вітки дерева хар-ють ієрархічний порядок об’єктів але не відображають ієрархічну залежність між об’єктами. Дворим. дендограма що описує залежність як в середені так і зовні. Агломеративна кластерна процедура пов’язана з обчисленням міри між всіма парами об’єктів і обєдн. на кожному кроці тієї пари для якої досягається min і max даних ф-й. Кластиризація здійснюється шляхом обєднаня спочатку роз’єднаних к об’єктів. Дивизивна кластерна процедура. пов’язана з обчисленням мір залежності між парами об’єктів і виділенням на кожному кроці тієї пари об’єктів для якої досягається min max даних ф-й. Кластер. здійснюється шляхом розбиття однієї групи об’єктів. Однорідною назив. сукуп. елементів якої формують під дією основних причин і умов а їх закони розподілу мають просту структуру. Неоднорідна- коли її різні елементи формуються під впливом різних причин і умов, або якщо вона представляється у вигляді обєднання деякої кількості однорідних сукупностей з більш простою структурою законів елементів. Оцінювальні індекси кластерного аналізу: а) величина зовнішнього критерію значимості-процент спів падання передбачених експертів з результатами процедур кластрног аналізу; б) в якості внутрішнього критерію значимості допускається кофенетичний коефіцієнт кореляції; в) міра відтворення- спеціальний коефіцієнт кореляції. Коефіцієнт подібності чи відмінності між і-ми спостереженнями діляться на 3 типи: dr (xut,xst)=( -де r додатне ціле число а m- кількість змінних. Коли r =1- манхетська відстань; r =2- томсономічна. Коефіцієнти асоціативності r(xut,xst)= призначені для оцінювання подібності иіж парами багатовимірних спостережень що описуються деякими значеннями у вигляді війкового коду. В коеф. асоціативності представляються коеф. загальної подібності. S- набув від [0;1] подібність між станами ознак xu,xw; W- вага, що приписана даній ознаці. Коефіцієнт кореляції до добутку стандартних відхилень: r = Приклади відстаней Наведемо ф-ї відст. і мір.: 1. 2. Зважена Евклідова відстань. 3. 4. Зважена відстань Махаланобіса 5. Хемінгова відстань:
6.Евристичні міри віддаленості – вони не є метриками через недотримання аксіом. Дискримінант ний аналіз. Методи дискр. аналізу виробл. деякі виріш. правила, що дозв. віднести запропоновані об’єкти до заданих класів. Вирішальні правила можуть бути стр. у вигляді ймов. (метод Баєса); простих функ. класиф. як у лін. дискр. анал. Фішера. Дискримін. ф-цій; у вигляді деяких характеристик; у вигляді ваг і зміщень нейронів. Нехай А1, А2 множина к об’єктів для простоти будемо розглядати два об’єкти причому кожному об’єкту поставимо у відпов. α=(α1, α2, … αn);η=(η1, η2, … ηn); Будемо вважати, що для кожної величини відомі певні параметри Q1=Q2. В більшості випадків під Q1 і Q2 розуміють багат. вибірок об’ємом n1 і n2 відпов. із А елементів xt={ xt1, xt2, …, xtm}; yt={ yt1, yt2, …, ytm} a Є А1, А2. Треба прим. вирішальне правило, яке дозв. віднос. об’єкти. Позначимо результат двовим. спостер. через Z={ zt1, zt2, …, ztm}; вирішальне правило заклечатись в тому, що спостер. Zt віднос. до того, що весь n-вимірний простір, в якому результат представл. буде розд. на 2 області на і R2; причому якщо результат поп. в R1 прийм. рішення про його належ. до А1, а якщо в R2 то до А2. Звичайно не викл. помилки, рішення про належн. об’єкта з А до А1 є помилк. і насправді позн. вартість встрат через С(А1/А2) та С(А2/А1). Припустимо, що ці об’єкти змішані у відпов. співвідн. а Є А2~q2$ a Є A1~q1. Q1+q2=1; як ймов. події яка,що взятий об’єкт буде належ. до А1.
|
||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 364; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.134.165 (0.008 с.) |

 xu≠xs; б). r(xu, xs)=1, xu=xs; в). r(xu, xs)= r(xs, xu), г). d(xs, xv)>d(xu, xs) =>r(xz, xv)≤ r(xu, xs).
xu≠xs; б). r(xu, xs)=1, xu=xs; в). r(xu, xs)= r(xs, xu), г). d(xs, xv)>d(xu, xs) =>r(xz, xv)≤ r(xu, xs).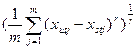 );коеф. відстані
);коеф. відстані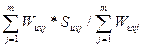 коеф. асоціативності
коеф. асоціативності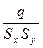 .
.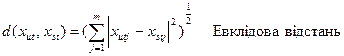
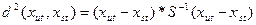 - звичайна відстань Махаланобіса
- звичайна відстань Махаланобіса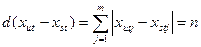 .
.


