
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перевірка лінійної регресії.Содержание книги Поиск на нашем сайте
Позначимо через
де
Показник (48) є мірою розсіювання дослідних даних навколо своїх частинних середніх, тобто мірою, що не залежить від вибраного вигляду регресії. В якості міри розсіювання дослідних даних навколо емпіричної регресійної прямої вибирається середній квадрат відхилень:
Обидва показники Якщо в генеральній сукупності існує лінійна регресія і умовні розподіли змінної y хоч би приблизно нормальні, то відношення середній квадратів
має F розподіл з Значення F пораховане за формулою (50) порівняне з критичним Якщо Розв’язок задач у випадку порушення класичних припущень(мультиколінеарність) При вивченні матричної лінійної регресії часто зустрічаються з наявністю лінійного зв’язку між всіма чи деякими пояснювальними змінними. Це явище називається мультиколінеарністю. 1) Для вимірювання стохастичної мультиколінеарності можна використати коефіцієнт множинної детермінації. При відсутності кореляції між пояснювальними змінними, тобто при відсутності мультиколінеарності, коефіцієнт множинної детермінації дорівнює сумі відповідних коефіцієнтів парної детермінації:
При наявності мультиколінеарності співвідношення (1) не виконується. Тому в якості міри мультиколінеарності можна запропонувати різницю:
Чим менша ця різниця, тим менша мультиколінеарність. 2) Інший показник розроблений А.Е.Хорлом. Він базується на використанні для вимірювання мультиколінеарності чисельника формули коефіцієнта множинної детермінації. А саме, що його можна представити наступним чином:
для Вираз є чисельником формули коефіцієнта парної кореляції між змінними
3) Також в якості показника мультиколінеарності можна також використати вираз (52), розділивши його на Чим більше М3, тим інтенсивніша мультиколінеарність. 4) Відомий показник мультиколінеарності, отримують з формули (5). Розділивши праву і ліву частини формули на
Розроблені ряд методів виключення чи зменшення мультиколінеарності: ü виключення змінних; ü лінійне перетворення змінних; ü виключення тренду; ü використання попередньої інформації; ü покрокова регресія; ü метод головних компонентів. Якщо зменшити мультиколінеарність не вдається, то до оцінок коефіцієнтів регресії і до значень регресії треба відноситись з великою обережністю. Дисперсійний аналіз Дисперсійний аналіз – статистичний метод дослідження вибіркових даних, що проводиться з метою виявлення і оцінки степені впливу на випадкову величину різних, одночасно діючих факторів. Розрізняють три моделі дисперсійного аналізу. Модель 1 – модель з постійними факторами, в якій всі Модель 2 – модель, в якій всі параметри Модель 3 – це модель, в якій хоч би один параметр Модель 1. Однофакторний дисперсійний аналіз Розглянемо випадок, коли на результат вимірювань впливає лише один фактор. Запишемо результати вимірювань деякої ознаки на р об’єктах у вигляді матриці у:
Такий запис матриці у означає, що на кожному об’єкті, що відповідає j -ій градації деякого фактору, проведна однакова кількість спостережень, рівна п. Основне рівняння однофакторного дисперсійного аналізу в умовах моделі 1 має вигляд:
що визначаєтья формулою
Статистична гіпотеза може бути сформульована наступним чином:
Перевірка гіпотези здійснюється за наступною схемою: 1) Обчислюють вибіркові середні
2) Знаходятьсуми квадратів відхилень вибіркових значень від відповідних середніх: а) суму, яка характеризує зміну, обумовлену досліджуваним фактором:
б) суму, яка характеризує зміну всередині кожної градації фактора:
в) суму, яка характеризує загальну зміну ознаки:
Якщо всі допущення про величини Відповідні дисперсії рівні:
Критерій, який використовують для перевірки гіпотези Н0, має вигляд:
При умові, що гіпотеза Н0 – вірна, розподіл критерію підлягає закону Фішера (F-розподіл). Гіпотеза відхиляється, якщо Модель 2. Оденофакторний дисперсійний аналіз Вибір об’єктів, що відповідають деяким градаціям досліджуваного фактору, рандомізований випадковий вибір факторів, що визначає випадковий характер факторних ефектів. Це приводить до зміни структури основного рівняння однофакторного дисперсійного аналізу. Воно набере вигляду де
|
||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 437; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

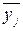 частинне середнє, що відповідає j -тому значенню пояснювальної змінної:
частинне середнє, що відповідає j -тому значенню пояснювальної змінної: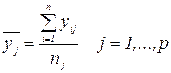 (47)
(47)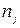 - число значень y, що відносяться до xjk (
- число значень y, що відносяться до xjk (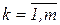 );
);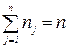 . Знайдемо тепер середній квадрат відхилень yij від їх частинних середніх.
. Знайдемо тепер середній квадрат відхилень yij від їх частинних середніх.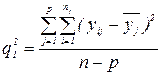 (48)
(48)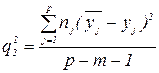 (49)
(49)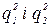 є незалежними статистичними оцінками однієї і тієї ж дисперсії
є незалежними статистичними оцінками однієї і тієї ж дисперсії 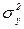 . Якщо
. Якщо 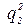 не набагато більше
не набагато більше 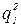 , то в якості гіпотетичної залежності може бути взята лінійна.
, то в якості гіпотетичної залежності може бути взята лінійна.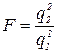 (50)
(50)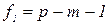 і
і 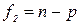 степенями вільності.
степенями вільності.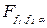 знайденим за таблицею F -розподілу при заданому рівні значущості
знайденим за таблицею F -розподілу при заданому рівні значущості 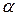 і
і 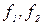 степенями вільності. Якщо
степенями вільності. Якщо 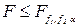 , то різниця між обома середніми квадратами відхилень статистично незначна і вибрана нами лінійна регресійна залежність може бути прийнята, як правдоподібна і як таке, що не протиречить дослідним даним.
, то різниця між обома середніми квадратами відхилень статистично незначна і вибрана нами лінійна регресійна залежність може бути прийнята, як правдоподібна і як таке, що не протиречить дослідним даним.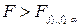 , то різниця між обома середніми квадратами відхилень суттєві і гіпотезу про лінійну залежність між змінними прийняти не можна. Існує інші критерії перевірки гіпотези про лінійність регресії.
, то різниця між обома середніми квадратами відхилень суттєві і гіпотезу про лінійну залежність між змінними прийняти не можна. Існує інші критерії перевірки гіпотези про лінійність регресії.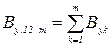 (51)
(51)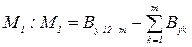 (52)
(52)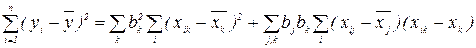
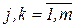 ,
, 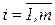 (53)
(53)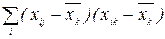 (54)
(54)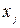 та
та 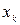 . При відсутності колінеарності загального показника мультиколінеарності можна використовувати різницю М2:
. При відсутності колінеарності загального показника мультиколінеарності можна використовувати різницю М2: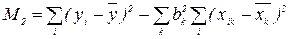 (55)
(55)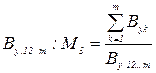 (56)
(56)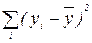 , отримаємо:
, отримаємо: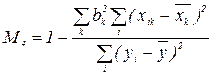 (57)
(57) можуть розглядатись, як невідомі сталі. Величина
можуть розглядатись, як невідомі сталі. Величина 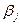 називається адитативною сталою.
називається адитативною сталою.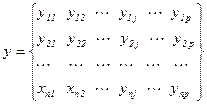 (4)
(4) , де
, де 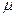 - генеральне середнє, (5)
- генеральне середнє, (5) ; (6)
; (6)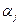 - ефект j- ї градації досліджуваного фактора, що визначається формулою
- ефект j- ї градації досліджуваного фактора, що визначається формулою 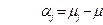 ; (7)
; (7)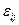 - випадкова незалежна величина, що відображає вплив на результати експеременту неконтрольованих факторів в даному спостереженні.
- випадкова незалежна величина, що відображає вплив на результати експеременту неконтрольованих факторів в даному спостереженні.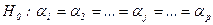 , тобто вплив досліджуваного фактора на всіх рівнях (градаціях) однаковий. Іншими словами, в умовах гіпотези H0 справедлива рівність:
, тобто вплив досліджуваного фактора на всіх рівнях (градаціях) однаковий. Іншими словами, в умовах гіпотези H0 справедлива рівність: 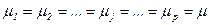 .
.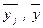 :
: , де N=np (8)
, де N=np (8)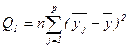 ; (за факторами) (9)
; (за факторами) (9)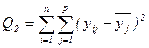 ; (залишкова) (10)
; (залишкова) (10)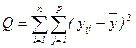 ; (загальна) (11)
; (загальна) (11) виконуються, то справедлива рівність
виконуються, то справедлива рівність 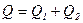 .
. (12)
(12)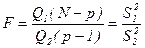 (13)
(13)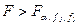 , де
, де 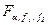 - таблиця значень F-розподілу при відповідному рівні значущості
- таблиця значень F-розподілу при відповідному рівні значущості 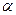 при степенях вільності
при степенях вільності 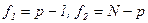 .
. , (14)
, (14)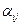 - значення випадкової величини (відхилення середнього значення ознаки на j - му об’єкті (mj) від генерального середнього, тобто
- значення випадкової величини (відхилення середнього значення ознаки на j - му об’єкті (mj) від генерального середнього, тобто  ).
).


