Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числові характеристики вибірки.Содержание книги Поиск на нашем сайте
Залежні змінні і незалежні. Незалежними змінними називаються змінні, які варіюються дослідником, тоді як залежні змінні – це змінні, які вимірюються чи регіструються. Якщо ще раз розглянути приклад з кількістю відвідувачів магазину, то інтенсивність реклами-це є незалежна змінна, а потік відвідувачів – залежна. Якщо в результат експерименту зареєстрували одне число, то відповідну випадкову величину прийнято називати одномірною або скалярною. Якщо ж результатом кожного експерименту (спостереження) є реєстрація цілого набору характеристик, то відповідну випадкову величину називають багатомірною чи векторною. Кількісна випадкова величина дозволяє вимірювати ступінь прояву властивості досліджуваного об'єкта у визначеній шкалі (інтервальна, шкала відношень). Ординальна випадкова величина дозволяє впорядкувати об'єкти, що досліджуються в ході випадкових експериментів по ступеню прояви в них властивостей, що аналізуються. Номінальна випадкова величина дозволяє розбивати об'єкти на однорідні класи, що не підлягають впорядкуванню. Метою будь-якого дослідження чи наукового аналізу є знаходження зв'язків (залежностей) між змінними, що вимірюються. Надійність взаємозалежності менш наглядне поняття, ніж величина залежності, але дуже важливе. Надійність показує наскільки ймовірно те, що залежність, подібна до знайденої, буде знову знайдена (підтвердиться) за даними іншої вибірки. Величина і надійність представляють собою дві різні характеристики між змінними. Але не можна сказати, що вони зовсім незалежні. В загальному можна стверджувати, що чим більша величина залежності (зв'язку) між змінними у вибірці, тим вона надійніша. 5. Групування даних. Описові статистики. Мінімум і максимум – це мінімальне і максимальне значення змінної. Середнє – сума значень змінної, поділене на n (число значень змінної):
Дисперсія вибірки або вибіркова дисперсія Стандартне відношення – Медіана вибірки – значення, що розбиває вибірку на дві рівні частини. Половина спостережень лежать вище медіани, половина – нижче. Обчислюється таким чином: вибірка впорядковується за зростанням, отримана послідовно xk, k=1,…2m+1, називається варіаційним рядом або порядковими статистиками. Якщо число спостережень непарне (2m+1), то медіана береться як xm+1, якщо парне 2т, то як Квантиль – це число хp, нижче якого знаходиться p -а частина (доля) вибірки. Мода – значення, яке найбільш часто зустрічається, тобто найбільш „модне” значення змінної. Асиметрія – це характеристика форми розподілу скошеності. Ексцес – характеристика форми розподілу, а саме міра гостроти піку
1. Етапи попередньої обробки даних. Попередня обробка результатів вимірювань чи спостережень необхідна для того, щоб надалі з найбільшою ефективністю, а головне – коректно, використовувати статистичні методи для побудови емпіричних залежностей. Суть попередньої обробки в основному полягає у відсіюванні грубих похибок вимірювань чи похибок, які виникають в результаті переписування цифрового матеріалу чи при вводі інформації в ЕОМ. Ще одним важливим моментом попередньої обробки є перевірка відповідності розподілу результатів вимірювань закону нормального розподілу. Після цього можна перейти до побудови елементарних формул, застосовуючи, наприклад, метод найменших квадратів В ході ПОД вирішують наступні підзадачі : 1. перетворення змінних описаних текстом номінальну та ординальну шкалу; 2. статичний опис поточних сукупностей з визначенням границь варіацій змінних; 3. аналіз спостережень що різко виділяються; 4. перевірка статистичної незалежності; 5. уніфікація типів змінних; 6. експеримент аналіз закону розподіл закону генеральної сукупності
Перевірка основних гіпотез. Під статистичною гіпотезою будь-яке твердження щодо генеральної сукупності, яке перевіряється на основі вибірки. Зроблений на основі статистичних даних висновок про те, що між кількома генеральними сукупностями або між емпіричним і теоретичним розподілом істотних відмінностей немає називають нульовою (основною) гіпотезою і позначають Н0. Гіпотезу, яка заперечує нульову, називають альтернативною гіпотезою і позначають буквою На. Ймовірність допустити помилку першого виду називають рівнем. Рівень значущості - це та мінімальна ймовірність, починаючи з якої можна вважати подію практично неможливою. Задачі першого типу пов’язані з перевіркою гіпотез про достовірність істотної відмінності між параметрами статистичних сукупностей. Задачі другого типу пов’язані з оцінкою ступеня розбіжності емпіричного і теоретичного розподілів. Перевірка гіпотези полягає в тому, що за вибірковими даними обчислюють значення деякої величини, яка має відомий стандартний розподіл. Цю величину називають статистикоюкритерію або просто значенням критерію. Перевірка статистичної гіпотези складається з наступних етапів: 1) оцінка вихідної інформації і опис статистичної моделі вибіркової сукупності; 2) визначення гіпотези Н0 і Н1; 3) задання рівня значущості "; 4) визначення за таблицями, рівнем значущості " і за альтернативною гіпотезою Н1 критичної області; 5) обчислення за вибіркою значення статистики; 6) порівняння значення статистики з критичною областю; 7) прийняття рішення: якщо значення статистики не входить в критичну область, то приймається гіпотеза Н0 і відкидається гіпотеза Н1, а якщо входить в критичну область, то заперечується гіпотеза Н0 і приймається гіпотеза Н1. 1. Видалення аномальних спостережень. Видалення спостережень, величина яких не порівнюються (узгоджуються) з розподілом основної маси даних. Ідентифікація аномальних спостережень дозволяє ще раз перевірити умови їх реєстрації і тим самим знайти і виправити помилку. Якщо ж помилку виправити не вдається, то дані просто виключаються із подальшої обробки як нетипові. Розглянута задача поділяється на два етапи: 1) Вияв „підозрілих” спостережень; 2) Перевірка статистичної значимості їх відмінності від основного набору даних 2. Перевірка випадковості (стохастичності) вибірки. Для перевірки, чи вибірка випадково вибрана із нормальної генеральної сукупності, чи вибірка випадково вибрана із нормальної генеральної сукупності, чи незалежні нормально розподілені випадкові величини, можна скористатись критерієм Аббе. Статистика критерія підраховується за формулою:
3. Графічне представлення даних. Для кількісного опису відмінностей між групами спостережень розроблені багато чисельні обчислювальні методи, що базуються на групуванні даних (наприклад, дисперсійний аналіз). Проте графічні засоби мають особливі переваги і дозволяють виявити закономірності, що важко піддаються кількісному опису і які важко знайти за допомогою обчислювальних процедур (наприклад, складні взаємозв'язки, виключення і аналогії). Для наглядності варіаційні ряди розподілу можуть бути зображені графічно у вигляді гістограми, полігону, огіви чи кумуляти. Гістограма служить для зображення варіаційного ряду розподілу, полігон – для дискретного варіаційного ряду, огіва – для ранджированого ряду, комулята – для накопичених частот (графік емпіричної функції розподілу). Графік складається з ізольованих точок. Їх можна з'єднати пунктирними прямими, щоб більш наглядно зобразити зміни pk при змінах хk. В проміжках між точками хk, а також поза областю (x1, x3) значення р=0. Такий графік називають ступеневий. У випадку неперервного розподілу на осі абсцис відкладають значення випадкової величини. Графік такого вигляду називається огіва. Для побудови графіка емпіричної щільності ймовірності на кожному інтервалі, як на основі, будують прямокутник, площа якого дорівнює або числу випадків, або відносній частоті. Графіки такого вигляду називають гістограмами. Іноді замість гістограми будують полігон, який отримують із гістограми якщо з'єднати відрізками прямих середини верхніх сторін прямокутника Діаграми розсіювання використовуються для візуального дослідження залежності між двома змінними дослідження залежності між двома змінними X і Y Дані зображаються крапками. Викиди. Ще одна важлива перевага діаграм розсіювання полягає в тому, що вони дозволяють знаходити „викиди” Нормальні ймовірності графіки – дозволяють візуально досліджувати, наскільки розподіл даних близький до нормального. Діаграми діапазонів. На діаграмах діапазонів показані діапазони значень чи стовпці помилок, що відносяться до визначених точок даних, у формі прямокутників чи відрізків. Як правило горизонтальні діаграми діапазонів використовуються для зображення часових проміжків, а не мінливість. Діаграми розмаху. На діаграмах розмаху чи так звані ящики-вуса, діапазони значень вибраної змінної (чи змінних) будуються окремо для груп спостережень, які визначаються значеннями категоріальної чи групової Стовпчикові діаграми – представляють собою послідовність значень у вигляді стовпців. Лінійні графіки – являють собою графіки однієї чи багатьох змінних, на яких окремі точки з'єднані лініями. Кругова діаграма – графік для представлення пропорцій. Діаграми пропущених значень та інтервалів. Трьохвимірний візуальний аналіз дозволяє аналізувати дані в трьох вимірному просторі. Категоризовані графіки дозволяють візуалізувати категоризовані дані, тобто дані розбиті на групи (категорії) за допомогою однієї чи декількох групуючи змінних.
1. Суть кореляційного аналізу Кореляція – це залежність між двома випадковоми величинами. Вона характеризується коефіцієнтами кореляції. Кореляційний аналіз полягає у визначенні тісноти зв’язку між двома випадковими величинами. Тіснота лінійного зв’язку в кореляційному аналізі характеризується спеціальним відносним показником, який називається коефіцієнтом кореляції. Значення коефіцієнта кореляції р належить відрізку [-1,1]. Якщо вибірковим коефіцієнтом кореляції, його позначають r і обчислюють за формулою
Значення rxy=0 говорить про відсутність лінійного зв’язку, можливо існує тісний нелінійний зв’язок, навіть нелінійний функціональний. Для перевірки нульової гіпотези обчислюють статистику Якщо Коефіцієнт детермінації – це є квадрат коефіцієнта кореляції, долю варіації, спільну для двох змінних, іншими словами “степінь” залежності двох змінних. Коефіцієнт множинної кореляції характеризує тісноту зв’язку однієї змінної із сукупністю інших.
де rі – парні лінійні коефіцієнти. По аналогії з парною кореляцією:R2- коефіцієнт детермінації. З допомогою коефіцієнта множинної кореляції не можна зробити висновок про характер взаємозв’язку, тобто про додатність чи від’ємність кореляції між змінними. Формула коефіцієнта множинної кореляції для будь-якого числа змінних має вигляд:
3. Частинні коефіцієнти кореляції. Задача визначення тісноти зв’язку між двома змінними при виключенні впливу інших змінних розв’язується за допомогою коефіцієнтів частинної кореляції. Розглянемо задачі дослідження частинної кореляції на прикладі взаємозв’язку трьох змінних а) для трьох змінних: 1. Між у та х1 при виключенні впливу х2: 2. Між у та х2 при виключенні впливу х1: 3. Між х1 та х2 при виключенні впливу у: 4. Нелінійна кореляція. Якщо між досліджувальними явищами існують нелінійні співвідношення, то так як і у випадку лінійного зв’язку, цікавляться тіснотою залежності і її сили. І коефіцієент кореляції, в прийнятій для лінійного зв’язку форми, не зможе відображати інтенсивність зв’язку. Тому виникає необхідність у розгляді показника інтенсивності зв’язку при нелінійних співвідношеннях. Таким показником зв’язку служить індекс кореляції.
а) для незгрупованих даних:
Індекс кореляції приймає значення в інтервалі Для згрупованих даних:
Множинна нелінійна кореляція. При нелінійних співвідношеннях індекс кореляції для трьох змінних запишеться так:
Коефіцієнт рангової кореляції. Поряд з розглядуваними лінійними і нелінійними коефіцієнтами кореляції існує ще ряд показників тісноти зв’язку, що широко застосовуються в економіці у тих випадках, коли ознакам деякого не можна однозначно приписати ті чи інші абсолютні значення. До них відноситься коефіцієнт рангової кореляції Спірмена При застосуванні методів рангової кореляції виходять не із точних кількісних оцінок значень ознак-змінних, а із рангів. Для цього елементи сукупності упорядковують у визначеному порядку у відповідності з деякими ознаками, що притаманні їм у неоднаковій мірі. Отриманий ряд елементів називають впорядкованим, а сам процес впорядкування називають “ ранжування ”, а кожному члену ряду присвоюється ранг, чи рангове число (порядковий номер). Якщо елемент володіє не однією, а двома ознаками х та у, то для дослідження їх впливу один на одного кожному елементу приписується два порядкових номери у відповідності з правилами рангування. Оскільки вивчається зв’язок між двома змінними, то коефіцієнт рангової кореляції Спірмена, який використовується назиавється парним. Коефіцієнт рангової кореляції Спірмена обчислюється за формулою:
На практиці трапляються випадки, коли два чи більше елементи сукупності мають однакові значення однієї і тієї ж ознаки і не можна знайти суттєву відмінність між ними. Елементи, називаються зв’язними, а а утворена з них група називається ланкою. Метод, який застосовується для приписування порядкового номера зв’язаним елементам, називається метод середніх рангів. При наявності об’єднаних рангів в коефіцієнт кореляції Спірмена вводиться поправка:
Тут А і В – поправочні коефіцієнти для зв’язок відповідно в послідовностях рангів v і w:
Коефіцієнт рангової кореляції може приймати значення в межах інтервалу Якщо rs=-1, то елементи двох послідовностей розміщені у зворотньому порядку і між ними повна неузгодженність. Це означає певну від’ємну кореляцію рангів. І коли rs=0, кореляція між рангами відсутня. Коефіцієнт рангової кореляції тим більше наближається до коефіцієнта парної кореляції, чим менше кореляційний зв’язок між змінними відрізняються від лінійного і чим сильніший цей зв’язок. Для нормально розподіленої генеральної сукупностіі при досить великому об’ємі вибірки
Метод рангової кореляції не потребує лінійної кореляції між змінними, Але необхідно, щоб функція регесії була монотонною. Коефіцієнт рангової кореляції Кендела. Інший коефіцієнт рангової кореляції
Коефіцієнт рангової кореляції Кендела можна обчислити за однією із еквівалентних формул:
Із (6) видно, що для визначення Величина 2. Індекс Фехнера. Ще одним простим показником ступеня взаємозв’язку між двома статистичними рядами є індекс Фехнера. Для його визначення по кожному ряду обчислюють середні
Відхилення, що дорівнюють 0, відносять пополам до v і до w. Легко переконатись, що Первага індекса Фехнера- простота обчислень. Але великий недолік в тому, що він враховує тільки кількість співвідношень і неспівпадань знаків відхилень. Тому рекомендується лише для приблизної оцінки зв’язку. Множинна лінійна регресія При існуванні лінійного співвідношення між змінними, загальний вираз рівняння множинної регресії (1) записується у вигляді:
Підставляючи (34) в (30) маємо:
або (35)
З системи нормальних рівняннь отримуємо b0 та b1:
Загальна процедура проведення регресійного аналізу включає в себе наступні етапи: 1. Формулювання економічної проблеми. На даному етапі формулюються гіпотези про залежність економічних явищ. Потім залежність кількісно оцінюється за допомогою методів регресійного аналізу, а саме яку форму і який вид може дана залежність. 2. Ідентифікація змінних. Визначають найбільш оптимальну кількість змінних, і класифікують їх на залежні і пояснювальні змінні. 3. Збір статичних даних. Приймається рішення про проведення досліджень за всією генеральною сукупністю чи за її вибіркою. Після цього приступають до збору даних для кожної змінної, включеної в аналіз. 4. Специфікація функції регресії. На цьому етапі дослідження, висувається конкретна гіпотеза про форму зв’язку. 5. Оцінка функції регресії. Визначаються числові значення параметрів регресії. Крім того, обчислюється ряд статичних показників, що характеризують точність регресійного аналізу. 6. Оцінка точності регресійного аналізу. На цьому етапі повинні бути зроблені висновки про точність результатів. 7. Економічна інтерпретація. Результати регресійного аналізу порівнюються з гіпотезами, що були сформульовані на першому етапі дослідження, і оцінюється їх правдоподібність з економічної точки зору. 8. Передбачення невідомих значень залежної змінної(прогноз). Прогноз отримують шляхом підстановки в регресій не рівняння, з чисельно оціненими параметрами, значень пояснювальної змінної. Дисперсійний аналіз Дисперсійний аналіз – статистичний метод дослідження вибіркових даних, що проводиться з метою виявлення і оцінки степені впливу на випадкову величину різних, одночасно діючих факторів. Розрізняють три моделі дисперсійного аналізу. Модель 1 – модель з постійними факторами, в якій всі Модель 2 – модель, в якій всі параметри Модель 3 – це модель, в якій хоч би один параметр Модель 1. Однофакторний дисперсійний аналіз Розглянемо випадок, коли на результат вимірювань впливає лише один фактор. Запишемо результати вимірювань деякої ознаки на р об’єктах у вигляді матриці у:
Такий запис матриці у означає, що на кожному об’єкті, що відповідає j -ій градації деякого фактору, проведна однакова кількість спостережень, рівна п. Основне рівняння однофакторного дисперсійного аналізу в умовах моделі 1 має вигляд:
що визначаєтья формулою
Статистична гіпотеза може бути сформульована наступним чином:
Перевірка гіпотези здійснюється за наступною схемою: 1) Обчислюють вибіркові середні
2) Знаходятьсуми квадратів відхилень вибіркових значень від відповідних середніх: а) суму, яка характеризує зміну, обумовлену досліджуваним фактором:
б) суму, яка характеризує зміну всередині кожної градації фактора:
в) суму, яка характеризує загальну зміну ознаки:
Якщо всі допущення про величини Відповідні дисперсії рівні:
Критерій, який використовують для перевірки гіпотези Н0, має вигляд:
При умові, що гіпотеза Н0 – вірна, розподіл критерію підлягає закону Фішера (F-розподіл). Гіпотеза відхиляється, якщо Модель 2. Оденофакторний дисперсійний аналіз Вибір об’єктів, що відповідають деяким градаціям досліджуваного фактору, рандомізований випадковий вибір факторів, що визначає випадковий характер факторних ефектів. Це приводить до зміни структури основного рівняння однофакторного дисперсійного аналізу. Воно набере вигляду де
Двофактоний ДА Складнішою моделлю дисперсійного аналізу є вивчення впливу на результати експерименту кількох факторів. Зокрема при аналізі впливу двох факторів структура моделі набуває вигляду:
де,
В двофакторному аналізі розрізняють багатосторонню (перехресну) класифікацію, коли таблиці вхідних даних В умовах моделі 1 фактори А, В, Загальна схема двофакторного дисперсійного аналізу (перехідна класифікація з повтореннями) 1. обчислюються вибіркові середні:
стовпцями;
рядками;
де 2. Визначаються суми квадратів відхилень, що обумовлені впливом різних факторів: а) б) в) г) д) Справедлива рівність
3.Тепер неважко знайти середні квадрати відхилень:
Перевірка гіпотез Модель 1.
Перевірка гіпотез здійснюється за критерієм:
Якщо Якщо виконується Модель ІІ Нульові гіпотези, що перевіряються запишемо так:
Відповідні критерії мають вигляд:
В умовах нульової гіпотези відношення
Модель ІІI. Перевіряються нульові гіпотези:
| ||
|
| Поделиться: |



 ,
,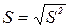 - корінь квадратний з дисперсії.
- корінь квадратний з дисперсії.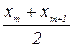 .
.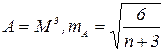 .
.
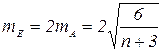 ;
; моментами розподілу
моментами розподілу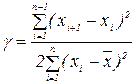 .
.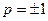 , то між випадковими величинами існує лінійний функціональний зв’язок. Якщо р=0, то між величинами x і y кореляції немає і їх називають некорельованими. Якщо р=1, то зв’язок називається функціональним. Для нормально розподіленої сукупності x і y некорельованість означає, що величини x і y незалежні. Додатний знак р вказує на прямий зв’язок між x і y, а від’ємний – на обернений зв’язок. Чим ближче коефіцієнт кореляції до одиниці, тим зв’язок між x і y тісніший.
, то між випадковими величинами існує лінійний функціональний зв’язок. Якщо р=0, то між величинами x і y кореляції немає і їх називають некорельованими. Якщо р=1, то зв’язок називається функціональним. Для нормально розподіленої сукупності x і y некорельованість означає, що величини x і y незалежні. Додатний знак р вказує на прямий зв’язок між x і y, а від’ємний – на обернений зв’язок. Чим ближче коефіцієнт кореляції до одиниці, тим зв’язок між x і y тісніший.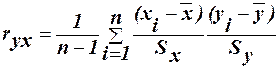 (1)
(1) , де п -обсяг вибірки. Статистика t має розподіл Стьюдента з
, де п -обсяг вибірки. Статистика t має розподіл Стьюдента з 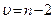 степенями вільності. Обчислене за формулою (3) значення t -критерію порівнюють порівнюють з критичним значенням
степенями вільності. Обчислене за формулою (3) значення t -критерію порівнюють порівнюють з критичним значенням  , знайденим за таблицею розподілу Стьюдента при заданому рівні значущості
, знайденим за таблицею розподілу Стьюдента при заданому рівні значущості  і числі ступенів вільності
і числі ступенів вільності 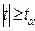 , то кульову гіпотезу про те, що між змінними x і y немає кореляційного зв’язку, відхиляють. Змінні x і y вважають залежними. Якщо
, то кульову гіпотезу про те, що між змінними x і y немає кореляційного зв’язку, відхиляють. Змінні x і y вважають залежними. Якщо 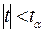 , то випадкові величини x і y не корельовані.
, то випадкові величини x і y не корельовані.
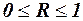 (7)
(7) , де (9)
, де (9) ,
, 
 (10)
(10)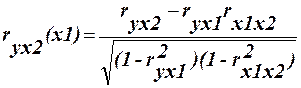 (11)
(11)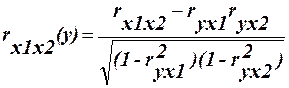 (12)
(12)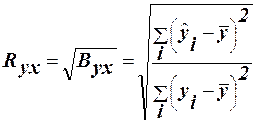 де
де 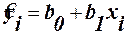 (14)
(14)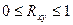 .
.
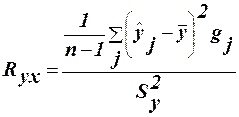 (16)
(16)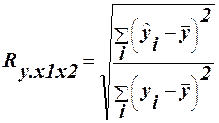 (18)
(18) тут – це значення регресії, обчислене за двома пояснювальними змінними. Показник Ry,12 вимірює тісноту нелінійної залежності змінної у одночасно від двох змінних х1 і х2 і дозволяє оцінити відповідність множинної нелінійної регресії емпіричним даним.
тут – це значення регресії, обчислене за двома пояснювальними змінними. Показник Ry,12 вимірює тісноту нелінійної залежності змінної у одночасно від двох змінних х1 і х2 і дозволяє оцінити відповідність множинної нелінійної регресії емпіричним даним.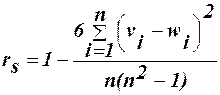 ` (1)
` (1)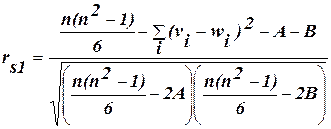 , (2)
, (2)
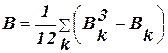 , k=1,2,….,p
, k=1,2,….,p . Якщо vi=wi, то rs=1. В цьому випадку є повна узгодженність між елементами двох послідовностей, кожний елемент займає одне і теж місце в обох рядах, що означає повну додатню кореляцію рангів.
. Якщо vi=wi, то rs=1. В цьому випадку є повна узгодженність між елементами двох послідовностей, кожний елемент займає одне і теж місце в обох рядах, що означає повну додатню кореляцію рангів.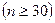 між двома коефіцієнтами існує наступне асимптотичне співвідношення:
між двома коефіцієнтами існує наступне асимптотичне співвідношення: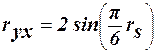 (3)
(3)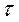 , не зв’язний з передумовою нормальності генеральної сукупності, був запропонований Кенделом. Він обчислюється за рангами vi і wi. При цьому елементи вибірки розміщують так, щоб послідовність рангів однієї із змінних являла собою натуральний ряд 1,2,...,п. Для кожного і -го члена послідовності рангів другій змінній встановлюємо числа рі та qi, що відображають прямий (1,2,...,10) та зворотній порядок розміщення наступних рангів. Потім підраховуємо суми цих чисел
, не зв’язний з передумовою нормальності генеральної сукупності, був запропонований Кенделом. Він обчислюється за рангами vi і wi. При цьому елементи вибірки розміщують так, щоб послідовність рангів однієї із змінних являла собою натуральний ряд 1,2,...,п. Для кожного і -го члена послідовності рангів другій змінній встановлюємо числа рі та qi, що відображають прямий (1,2,...,10) та зворотній порядок розміщення наступних рангів. Потім підраховуємо суми цих чисел  ,
,  ,а також різницю S=P-Q. Коефіцієнт рангової кореляції
,а також різницю S=P-Q. Коефіцієнт рангової кореляції 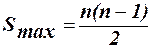 (4)
(4) (5)
(5)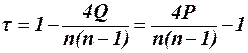 (6)
(6)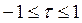 . Тяжко дати рекомендації, який коефіцієнт краще використовувати на практиці. Вони (rs і
. Тяжко дати рекомендації, який коефіцієнт краще використовувати на практиці. Вони (rs і 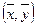 , і визначають знаки відхилень
, і визначають знаки відхилень  та
та 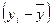 . Позначимо через v кількість співпадань, а через w - кількість неспівпадань знаків різниць. Індекс Фехнера і визначається за формулою
. Позначимо через v кількість співпадань, а через w - кількість неспівпадань знаків різниць. Індекс Фехнера і визначається за формулою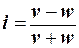 (7)
(7)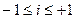 . При і>0 маємо додатню кореляцію, а при і<0 – від’ємну, а при і=0 зв’язок відсутній.
. При і>0 маємо додатню кореляцію, а при і<0 – від’ємну, а при і=0 зв’язок відсутній.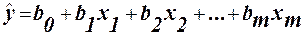 (29)
(29)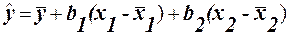
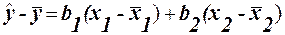
 (36)
(36) (37)
(37) можуть розглядатись, як невідомі сталі. Величина
можуть розглядатись, як невідомі сталі. Величина 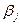 називається адитативною сталою.
називається адитативною сталою.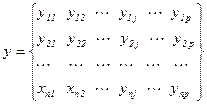 (4)
(4) , де
, де 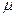 - генеральне середнє, (5)
- генеральне середнє, (5) ; (6)
; (6)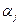 - ефект j- ї градації досліджуваного фактора, що визначається формулою
- ефект j- ї градації досліджуваного фактора, що визначається формулою 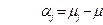 ; (7)
; (7)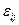 - випадкова незалежна величина, що відображає вплив на результати експеременту неконтрольованих факторів в даному спостереженні.
- випадкова незалежна величина, що відображає вплив на результати експеременту неконтрольованих факторів в даному спостереженні.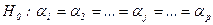 , тобто вплив досліджуваного фактора на всіх рівнях (градаціях) однаковий. Іншими словами, в умовах гіпотези H0 справедлива рівність:
, тобто вплив досліджуваного фактора на всіх рівнях (градаціях) однаковий. Іншими словами, в умовах гіпотези H0 справедлива рівність: 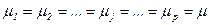 .
.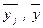 :
: , де N=np (8)
, де N=np (8)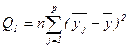 ; (за факторами) (9)
; (за факторами) (9)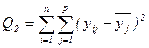 ; (залишкова) (10)
; (залишкова) (10)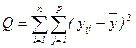 ; (загальна) (11)
; (загальна) (11) виконуються, то справедлива рівність
виконуються, то справедлива рівність 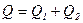 .
. (12)
(12)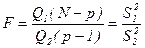 (13)
(13)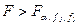 , де
, де 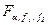 - таблиця значень F-розподілу при відповідному рівні значущості
- таблиця значень F-розподілу при відповідному рівні значущості 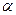 при степенях вільності
при степенях вільності 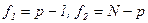 .
. , (14)
, (14)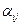 - значення випадкової величини (відхилення середнього значення ознаки на j - му об’єкті (mj) від генерального середнього, тобто
- значення випадкової величини (відхилення середнього значення ознаки на j - му об’єкті (mj) від генерального середнього, тобто  ).
). (27)
(27)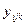 - значення ознаки y в і -му експеременті j -му рівні впливу фактора А і на k -му рівні впливу фактора В;
- значення ознаки y в і -му експеременті j -му рівні впливу фактора А і на k -му рівні впливу фактора В; 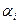 -ефект впливу факторів А на і -му рівні,
-ефект впливу факторів А на і -му рівні,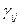 -ефект одночасного впливу факторів А і В;
-ефект одночасного впливу факторів А і В;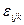 -випадкова компонента (варіація в середині окремої групи).
-випадкова компонента (варіація в середині окремої групи).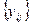 кожний j -й стовпець (j -та градація фактора В) містить однакову кількість груп, що відповідають градаціям і -го фактора А, та ієрахічну класифікацію, коли фактор В (другосторонній в рамках даної задачі) згрупований всередині головного А. В ієрархічній класифікації число градацій фактора В, що фіксуються всередині різних градацій фактора А, може бути поодиноким.
кожний j -й стовпець (j -та градація фактора В) містить однакову кількість груп, що відповідають градаціям і -го фактора А, та ієрахічну класифікацію, коли фактор В (другосторонній в рамках даної задачі) згрупований всередині головного А. В ієрархічній класифікації число градацій фактора В, що фіксуються всередині різних градацій фактора А, може бути поодиноким. розглядаються, як фіксовані, щодо моделі 2 – як випадкові. Для змішаної моделі одному із факторів приписується систематичний вплив, другому випадковий. Для визначеності, допускають, що в моделі 3 фактор В - фіксований, а фактор А, і їх взаємодія АВ - випадковий.
розглядаються, як фіксовані, щодо моделі 2 – як випадкові. Для змішаної моделі одному із факторів приписується систематичний вплив, другому випадковий. Для визначеності, допускають, що в моделі 3 фактор В - фіксований, а фактор А, і їх взаємодія АВ - випадковий. середнє значення ознаки у для кожного блока; (28)
середнє значення ознаки у для кожного блока; (28) середнє значення ознаки у за (29)
середнє значення ознаки у за (29) середнє значення ознаки у за (30)
середнє значення ознаки у за (30)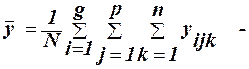 загальна середня ознаки у (31)
загальна середня ознаки у (31) .
. -вплив фактору А; (32)
-вплив фактору А; (32)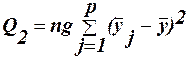 - вплив фактору В; (33)
- вплив фактору В; (33)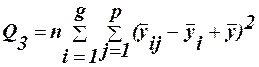 -вплив взаємодії факторів АВ; (34)
-вплив взаємодії факторів АВ; (34)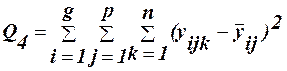 -зміни, пов’язані з (35) відмінностями всеридині комірки;
-зміни, пов’язані з (35) відмінностями всеридині комірки;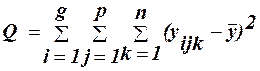 -загальна зміна, даної ознаки. (36)
-загальна зміна, даної ознаки. (36)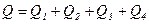 . Величина
. Величина  відповідає (g-1) -степеней вільностей;
відповідає (g-1) -степеней вільностей;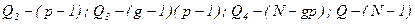 .
.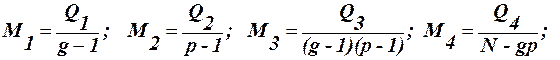 (37)
(37)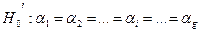

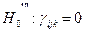
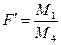

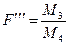
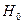 вірна то дані величини підлягають F розподілу.
вірна то дані величини підлягають F розподілу.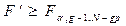

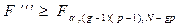 то вплив відповідно факторів а,в і їх взаємодія вважаються суттєвими.
то вплив відповідно факторів а,в і їх взаємодія вважаються суттєвими.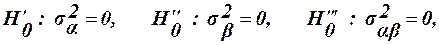 (41)
(41)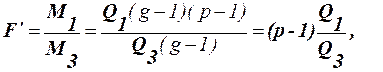
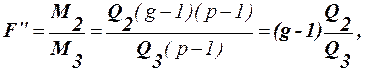 (42)
(42)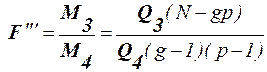 ,
, ,
, 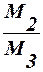 і
і  мають F -розподіл з відповідними степенями вільності. Гіпотези
мають F -розподіл з відповідними степенями вільності. Гіпотези 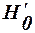 ,
,  ,
,  відхиляються (при заданому рівні значущості
відхиляються (при заданому рівні значущості 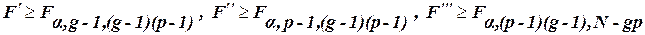 (43)
(43)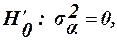
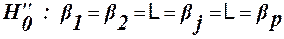 ,
,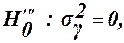 (44)
(44)