
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однофакторний ДА з нерівною кількістю спостереженьСодержание книги
Поиск на нашем сайте
Загальна схема аналізу лишається такою ж, деякі зміни вносяться лише у формули, за якими обчислюються оцінки середніх і суми квадратів відхилень:
Якщо величина F-критерію перевищила критичне значення Більш загальний розв’язок задачі дає метод Шеффе(S- метод). За його допомогою можна побудувати довірчі інтервали для будь-якої лінійної комбінації середніх:
Фунція Як і раніше, будемо допускати, що
Вибірковою оцінкою D(H) є величина
Коли провести
Двофактоний ДА Складнішою моделлю дисперсійного аналізу є вивчення впливу на результати експерименту кількох факторів. Зокрема при аналізі впливу двох факторів структура моделі набуває вигляду:
де,
В двофакторному аналізі розрізняють багатосторонню (перехресну) класифікацію, коли таблиці вхідних даних В умовах моделі 1 фактори А, В, Загальна схема двофакторного дисперсійного аналізу (перехідна класифікація з повтореннями) 1. обчислюються вибіркові середні:
стовпцями;
рядками;
де 2. Визначаються суми квадратів відхилень, що обумовлені впливом різних факторів: а) б) в) г) д) Справедлива рівність
3.Тепер неважко знайти середні квадрати відхилень:
Перевірка гіпотез Модель 1.
Перевірка гіпотез здійснюється за критерієм:
Якщо Якщо виконується Модель ІІ Нульові гіпотези, що перевіряються запишемо так:
Відповідні критерії мають вигляд:
В умовах нульової гіпотези відношення
Модель ІІI. Перевіряються нульові гіпотези:
Прийняття рішення здійснюється так, як і в моделях 1 і 2. Існують ще різновиди перехресної класифікації. А саме: Ø перехресна класифікація (ПК) з одним повторенням в комірці. Ø ПК з нерівною кількістю спостережень в комірках. Ієрархічна класифікація результатів спостережень застосовується в дисперсійному аналізі в тих випадках, коли один фактор згрупований всередині іншого „головного” фактора. основне рівняння прийнятої моделі дисперсійного аналізу мають вигляд:
де
Дисперсію у запишемо у вигляді суми:
Перевіряємо гіпотези:
Визначаємо суми квадратів відхилень:
де
Величина
Статистики при виконанні відповідних нульових гіпотез, мають F -розподіл з степенями вільності
Коваріаційний аналіз. Коваріація між двома вибірками випадкових величин обчислюється за формулою:
де Коваріація вибірки самої з собою називається дисперсією. Коваріація може бути як додатньою, так і від’ємною. В більш широкому змісті коваріацією називають сукупність трьох статичних показників: середніх арифметичних Коваріаційний аналіз включає три основних етапи: 1) дисперсійний аналіз X, Y та добутків XY; 2) розклад залишкової дисперсії Cz за рядом у (залишок 1) на суму квадратів відхилень, обумовлену регресією Y по X, що позначається Cb ісуму квадратів відхилень від регресії
3) приведення фактичних середніх за рядом Y до повного вирівнювання умов експерименту за рядом Х. коваріаційний аналіз (КА) – це статистичний метод оцінки впливу на випадкову величину різних одночасно діючих факторів, одні з яких задані якісно, а інші можуть бути виміряні кількісно. Тобто, КА можна розглядати, як комбінацію дисперсійного та регресійного аналізів. Суму квадратів відхилень, зумовлену регресією Y на X визначають за формулою:
Суму квадратів випадкового змінювання, тобто суму квадратів відхилень від регресії, знаходить як різницю Коеіцієнт регресії Результативну ознаку вирівнюють за співвідношенням
Y1 – коректоваі дані; byx – коефіцієнт регресії; Y – фактичні дані; (2.) Основна модель КА, що узагальнює дисперсійний та регресійний підходи, має вигляд:
де Y, X, β мають той же зміст, що і моделі ДА; а z’γ – визначає вклад факторів, що піддаються кількісному дослідженню, при цьому z – значення факторів (регресорів), γ – коефіцієнти регресії Y на z. Далі будемо допускати, що коефіцієнти регресії не залежать від градацій якісного фактору, що задають розбиття вхідних даних на р груп:
Основні припущення КА: 1) Y має нормальний розподіл з параметрами 2) Y має нормальний розподіл з параметрами Як і в дисперсійному і регресійному аналізах, розподіл e також допускається нормальним з параметрами Припущення (1) відповідає нульовій гіпотезі Якщо ж Основна модель КА зручно розглядати на прикладі одно факторного аналізу з однією незалежною змінною (регресором):
де
Перевірка гіпотези І. Визначаємо суми квадратів і добутків відхилень, що відображають змінювання Y і z, а) Всередині груп (градацій)
де б) Між групами:
де
ІІ. Якщо гіпотеза
має F-розподіл з f1=1, f2=N-p-1 степенями вільності. Гіпотеза про рівність нулю коефіцієнта регресії g відхиляється, якщо обчислене значення критерія перевищить табличне Перевірка гіпотези
Суми квадратів „між групами” і „всередині груп” повинні бути скореговані так, щоб вплив незалежної змінної z було б виключено: а=а1+а2; b=b1+b2; c=c1+c2 (14) Відповідно:
Статистика Розглянуту схему можна узагальнити на випадок, коли класифікація спостережень виконана за двома і більше факторами.
|
||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 263; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.52.26 (0.008 с.) |

 (15)
(15) (16)
(16) (17)
(17) (18)
(18) (19)
(19)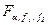 , то нульова гіпотеза відхиляється. В цьому випадку допускають, що існує, в крайньому разі, хоч би одна пара середніх, наприклад,
, то нульова гіпотеза відхиляється. В цьому випадку допускають, що існує, в крайньому разі, хоч би одна пара середніх, наприклад,  і
і  , для яких
, для яких  .
. (20)
(20) , визначена таким чином, називається контрастом. Вибіркову оцінку
, визначена таким чином, називається контрастом. Вибіркову оцінку  величинами
величинами 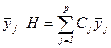 (21)
(21) належні і нормально розподілені, а
належні і нормально розподілені, а 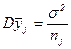 , звідси випливає, що
, звідси випливає, що (23)
(23) , де (24)
, де (24) , (25)
, (25) - об’єм вибірки, що відповідає j- й градації, досліджуваного фактору. Довірчий інтервал велечини
- об’єм вибірки, що відповідає j- й градації, досліджуваного фактору. Довірчий інтервал велечини  , де
, де (26)
(26) таких порівняннь, то можна виділити всі „контрастні” значення
таких порівняннь, то можна виділити всі „контрастні” значення  і тим самим виявити джерело неоднорідності середніх.
і тим самим виявити джерело неоднорідності середніх. (27)
(27)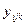 - значення ознаки y в і -му експеременті j -му рівні впливу фактора А і на k -му рівні впливу фактора В;
- значення ознаки y в і -му експеременті j -му рівні впливу фактора А і на k -му рівні впливу фактора В; 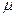 -загальна середня величина ознаки у;
-загальна середня величина ознаки у; 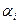 -ефект впливу факторів А на і -му рівні,
-ефект впливу факторів А на і -му рівні,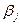 -ефект впливу фактора В на j- му рівні;
-ефект впливу фактора В на j- му рівні;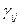 -ефект одночасного впливу факторів А і В;
-ефект одночасного впливу факторів А і В;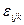 -випадкова компонента (варіація в середині окремої групи).
-випадкова компонента (варіація в середині окремої групи).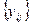 кожний j -й стовпець (j -та градація фактора В) містить однакову кількість груп, що відповідають градаціям і -го фактора А, та ієрахічну класифікацію, коли фактор В (другосторонній в рамках даної задачі) згрупований всередині головного А. В ієрархічній класифікації число градацій фактора В, що фіксуються всередині різних градацій фактора А, може бути поодиноким.
кожний j -й стовпець (j -та градація фактора В) містить однакову кількість груп, що відповідають градаціям і -го фактора А, та ієрахічну класифікацію, коли фактор В (другосторонній в рамках даної задачі) згрупований всередині головного А. В ієрархічній класифікації число градацій фактора В, що фіксуються всередині різних градацій фактора А, може бути поодиноким. розглядаються, як фіксовані, щодо моделі 2 – як випадкові. Для змішаної моделі одному із факторів приписується систематичний вплив, другому випадковий. Для визначеності, допускають, що в моделі 3 фактор В - фіксований, а фактор А, і їх взаємодія АВ - випадковий.
розглядаються, як фіксовані, щодо моделі 2 – як випадкові. Для змішаної моделі одному із факторів приписується систематичний вплив, другому випадковий. Для визначеності, допускають, що в моделі 3 фактор В - фіксований, а фактор А, і їх взаємодія АВ - випадковий. середнє значення ознаки у для кожного блока; (28)
середнє значення ознаки у для кожного блока; (28) середнє значення ознаки у за (29)
середнє значення ознаки у за (29) середнє значення ознаки у за (30)
середнє значення ознаки у за (30)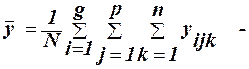 загальна середня ознаки у (31)
загальна середня ознаки у (31) .
. -вплив фактору А; (32)
-вплив фактору А; (32)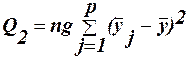 - вплив фактору В; (33)
- вплив фактору В; (33)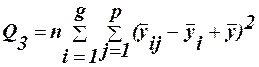 -вплив взаємодії факторів АВ; (34)
-вплив взаємодії факторів АВ; (34)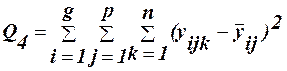 -зміни, пов’язані з (35) відмінностями всеридині комірки;
-зміни, пов’язані з (35) відмінностями всеридині комірки;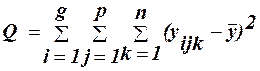 -загальна зміна, даної ознаки. (36)
-загальна зміна, даної ознаки. (36)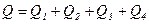 . Величина
. Величина  відповідає (g-1) -степеней вільностей;
відповідає (g-1) -степеней вільностей;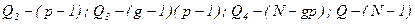 .
.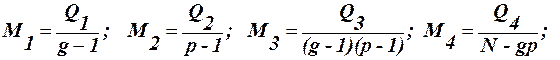 (37)
(37)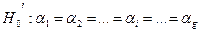


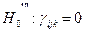
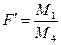

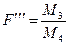
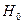 вірна то дані величини підлягають F розподілу.
вірна то дані величини підлягають F розподілу.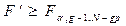

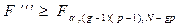 то вплив відповідно факторів а,в і їх взаємодія вважаються суттєвими.
то вплив відповідно факторів а,в і їх взаємодія вважаються суттєвими.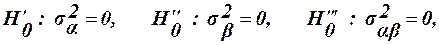 (41)
(41)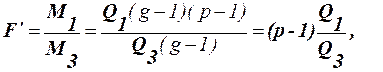
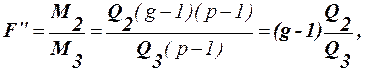 (42)
(42)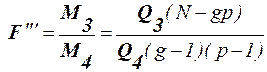 ,
, ,
, 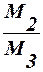 і
і  мають F -розподіл з відповідними степенями вільності. Гіпотези
мають F -розподіл з відповідними степенями вільності. Гіпотези 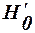 ,
,  ,
,  відхиляються (при заданому рівні значущості
відхиляються (при заданому рівні значущості 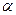 ), якщо
), якщо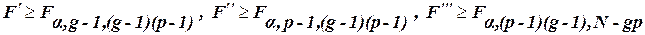 (43)
(43)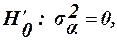
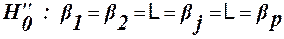 ,
,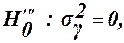 (44)
(44)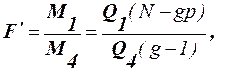
 (45)
(45) .
. (46)
(46) -ефект j -го рівня фактора В в межах і -ої градації фактора А;
-ефект j -го рівня фактора В в межах і -ої градації фактора А; -ефект неконтрольованих факторів.
-ефект неконтрольованих факторів. (47)
(47) (48)
(48) (49)
(49) (50)
(50) (51)
(51) (52)
(52) (53)
(53)  (54)
(54) відображає вплив фктора А,
відображає вплив фктора А,  -вплив фактору В,
-вплив фактору В, 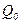 -характеризує зміну всередині комірок. Середні квадрати знаходяться за формулами:
-характеризує зміну всередині комірок. Середні квадрати знаходяться за формулами: (55)
(55) (56)
(56)
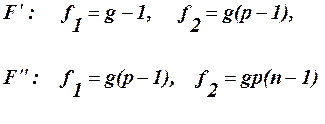 (57)
(57) (1)
(1) компоненти векторів х та у, п - чисельність вибірки.
компоненти векторів х та у, п - чисельність вибірки.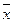 та
та  , сум квадратів відхилень
, сум квадратів відхилень  і
і  і суми добутків відхилень
і суми добутків відхилень  . Паралельний розклад цих величин за факторами змін і складає суть коваріаційного аналізу.
. Паралельний розклад цих величин за факторами змін і складає суть коваріаційного аналізу. (залишок 2);
(залишок 2); (2)
(2) (3)
(3)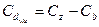 .
. (4)
(4)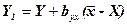 (5)
(5) - різниця між середнім значенням незалежної змінної х та її фактичним значенням.
- різниця між середнім значенням незалежної змінної х та її фактичним значенням. (6)
(6) .
.

 .
. , а припущення (2) – гіпотезі
, а припущення (2) – гіпотезі 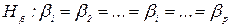 . Якщо
. Якщо  виконується, то перевірка
виконується, то перевірка  зводиться до загального дисперсійного аналізу.
зводиться до загального дисперсійного аналізу.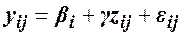 (7)
(7) - ефект і - ї градації фактора А;
- ефект і - ї градації фактора А; - ефект, обумовлений дією змінної z;
- ефект, обумовлений дією змінної z; - коефіцієнт регресії;
- коефіцієнт регресії; - ефект неконтрольованих факторів;
- ефект неконтрольованих факторів;  .
. : g = 0 здійснюється за наступною схемою:
: g = 0 здійснюється за наступною схемою: ;
; 
 (8)
(8) ;
;  (9)
(9) ;
;  (10)
(10) (11)
(11) ;
; 
 (12)
(12) (13)
(13) .
. в умовах
в умовах  ;
;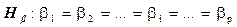 .
. ;
;  ;
;  (15)
(15) в умовах гіпотези
в умовах гіпотези  має F- розподіл з f1=p-1, f2=N-p-1 степенями вільності.
має F- розподіл з f1=p-1, f2=N-p-1 степенями вільності.


