
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: відношення порядку. Впорядковані множини. Точна верхня і точна нижня грані. Дійсні числа.Содержание книги
Поиск на нашем сайте
Необхідні відомості: Визначення бінарного відношення і відношення порядку. Визначення верхньої та нижньої граней, точної верхньої та точної нижньої граней. Визначення дійсних чисел, аксіоми повноти. Теорема о верхній грані.
Задачі 1. Бінарне відношення і відношення порядку 1.1 Нехай Х=[0,1], побудувати бінарне відношення 1.2 Нехай X=N ввести на N відношення порядку на основі подільності чисел і довести, що відношення – відношення порядку. Чи буде N впорядкованою множиною? 2. Точна верхня та точна нижня грані 2.1 2.2 Нехай 3. Визначення дійсних чисел. Теорема о верхній грані. 3.1 Перевірити, що Q задовольняє усім аксіомам дійсних чисел окрім аксіоми повноти. 3.2 Довести, що принцип верхньої грані еквівалентний аксіомі повноти.
Завдання для самостійної роботи. 1. Нехай x=R1 побудувати бінарне відношення 2. Нехай Х – множина усіляких множин. Показати, що відношення включення – відношення порядку. Чи буде Х впорядкованим? 3. Нехай Х=R2. Розглянемо відношення 4. Нехай Х=R3. Розглянемо відношення 5. Ввести відношення порядку подібно до задачі 4 на Rn. 6. 7. Нехай 8. Нехай х, у – множини із задачі 7, то або існує max x, або існує min y. 9. Показати на прикладі, що аксіома повноти не виконується на множині Z. 10.Який вид має мати множина А – підмножина R1, щоб на ньому виконувалася аксіома повноти. 11. Нехай на R3 введено відношення порядку
Практичне заняття № 4 Тема: Верхня та нижня грані множини. Точна нижня та верхня грані. Основні відомості: 1. Аксіома неперервності. 2. Визначення верхньої та нижньої грані множини. 3. Визначення sup та inf множини. 4. Теорема про існування sup та inf обмеженої множини. 5. Принцип Архімеда.
Задачі:
1. Обмеженість. Верхні, нижні грані. Мінімальні, максимальні елементи. 1.1. Довести, що множина всіх 1.2. Довести обмеженість множини X= 1.3. Знайти точні верхні та нижні грані множин Найбільші та найменші елементи цих множин, якщо такі елементи існують. 2. Точні грані. 2.1 Нехай
2.2 Нехай
2.3 Нехай
2.4 Довести, що множина всіх правильних раціональних дробів
Завдання для самостійної роботи. Довести обмеженість множини: 1. 2. 3. 4. Довести, що множина 5. Довести, що множина 6. Довести, що множина Знайти точні верхні і нижні грані множин, найбільші і найменші елементи, якщо такі існують: 7. 8. 9. 10. 11. 12. 13. Нехай 14. Нехай 15. Нехай 16. Нехай 17. Нехай 18. Нехай 19. В умовах задачі 18 довести, що: 20. 21. В умовах задачі 20 довести, що: 22.
Практичне заняття №5 Тема: Дійсні числа. Формули скороченого множення. Основні нерівності. Основні відомості: 1. Визначення множини дійсних чисел. 2. Формули скороченого множення. 3. 4. 5. 6.
Задачі: 1.Розв'зати завдання: 1.1.Представити у вигляді суми трьох радикалів: 1.2.Обчислити: 1.3.Довести 2 В наступних задачах знайти суму: 2.1. 2.2. 3. Довести нерівності: 3.1. 3.2. Вказівка: взяти 3.3
Завдання для самостійної роботи. 1. Довести: 2. Спростити: 3.
4. Спростити: 5. Довести:
6. Довести a3+b3+c3=3abc, якщо a+b+c=0. 7. Довести, що якщо 8. Показати, що при непарному 9. Знайти суму 10.Знайти суму 11.Знайти суму: 12.Знайти суму: 13.Чому дорівнює 14.Знайти доданок:
Довести нерівності: 15. 17. 18. 19. 20. 21.
22. 23. 24. 25. Нехай Вказівка: показати, що Практичне заняття №6
|
||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 364; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.13.194 (0.008 с.) |

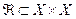 зобразити його на площині.
зобразити його на площині.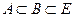 , де Е- впорядкована множина, довести
, де Е- впорядкована множина, довести 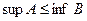
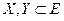 , де Е- впорядкована множина для будь-яких
, де Е- впорядкована множина для будь-яких 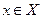 ,
, 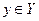 ,
, 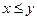 то
то 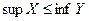 .
. на R2 таке, що (х, у)
на R2 таке, що (х, у) 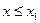 . Чи буде це відношення відношенням порядку?
. Чи буде це відношення відношенням порядку?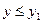 ,
, 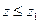 . Чи буде це відношення відношенням порядку, а множина Х - впорядкованою?
. Чи буде це відношення відношенням порядку, а множина Х - впорядкованою?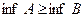 .
.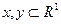 і для будь-яких
і для будь-яких 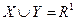 , то
, то  .
.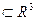 і будь-який елемент із А знаходиться в відношенні з будь-яким елементом із В, то існує елемент (x0, y0, z0)
і будь-який елемент із А знаходиться в відношенні з будь-яким елементом із В, то існує елемент (x0, y0, z0) 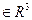 такий, що
такий, що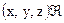
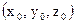
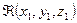 для
для 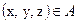 і
і 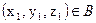 .
.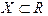 обмежена, тоді і тільки тоді, коли існує таке
обмежена, тоді і тільки тоді, коли існує таке 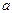 , що для
, що для виконується нерівність
виконується нерівність 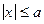 .
.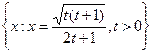 .
.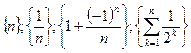 ,
,  .
.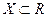 та – X - множина чисел, протилежних числам
та – X - множина чисел, протилежних числам 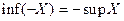 .
.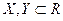 та X+Y=
та X+Y= 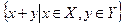 . Довести
. Довести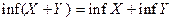
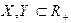 та
та 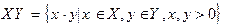 .Довести, що
.Довести, що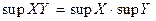
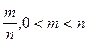
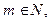
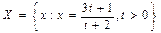
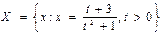

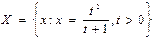 необмежена зверху.
необмежена зверху.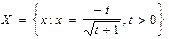 необмежена знизу.
необмежена знизу.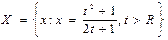 необмежена зверху і знизу.
необмежена зверху і знизу.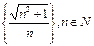
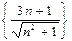 ,
, 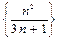 ,
, 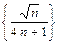 ,
, 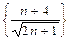 ,
, 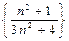 ,
, 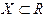 і
і 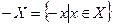 .Довести, що
.Довести, що 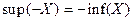 .
. і
і 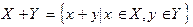 . Довести, що
. Довести, що  .
.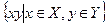 .Довести, що
.Довести, що 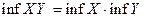 .
. і
і 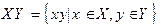 .Довести, що
.Довести, що 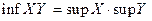 .
.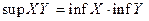 .
.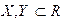 і
і 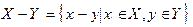 .Довести, що
.Довести, що 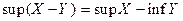 .
.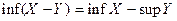 .
. обмежено і
обмежено і 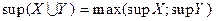 .
.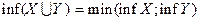 .
.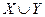 обмежено і
обмежено і 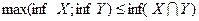
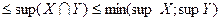 .
.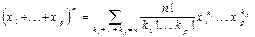
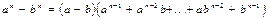
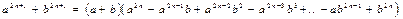
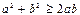 7.
7. 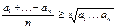 8.
8. 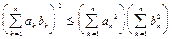
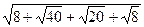
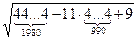
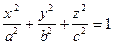 , якщо
, якщо  і
і 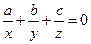
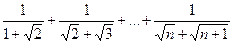
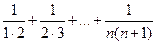 2.3.
2.3. 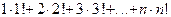
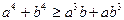
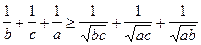
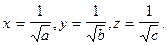
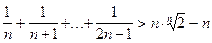
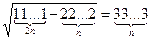
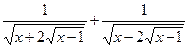
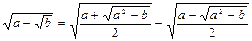

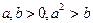
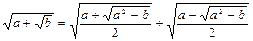

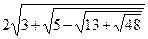
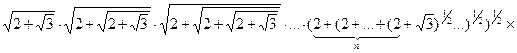
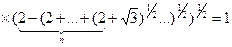
 задовольняють співвідношенню
задовольняють співвідношенню 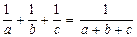 , то серед a, b, c знайдуться два числа, сума яких дорівнює 0.
, то серед a, b, c знайдуться два числа, сума яких дорівнює 0. з рівності
з рівності 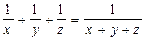 виходить, що
виходить, що 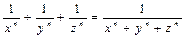
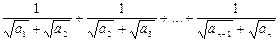 де
де  - арифметична прогресія.
- арифметична прогресія.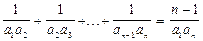 де
де 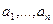 - арифметична прогресія.
- арифметична прогресія.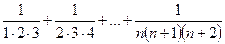
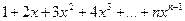
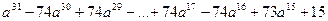 при
при 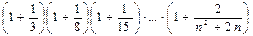
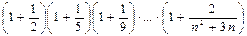
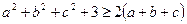 16.
16. 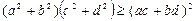
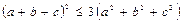
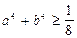 , якщо
, якщо 
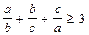 ,
, 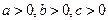
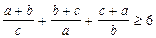 ,
, 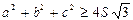 , де
, де  - площа трикутника.
- площа трикутника.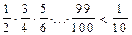
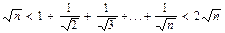
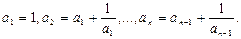 . Довести 14<a100<15.
. Довести 14<a100<15.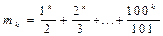
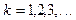 довести, що
довести, що 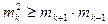
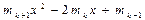 приймає невід'ємні значення при всіх
приймає невід'ємні значення при всіх 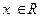 .
.


