
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Властивості замкнених множин.Содержание книги
Поиск на нашем сайте 1. Множини Е, Ø - замкнені; 2. 3. Доведення провести самостійно. Зауваження. Існують підмножини, що не є ні замкненими ні відкритими. Наприклад: Означення. Околом точки Теорема. Для того, щоб підмножина А простору Доведення. Нехай А - окіл кожної своєї точки. Тоді разом з точкою Означення. Замиканням
Приклад: Означення. Точка Теорема. Замкнена множина містить усі свої граничні точки. Доведення. Нехай Теорема. Нижче Лекція №7. Неперервні функції. Гомеоморфізми. Означення неперервної функції та її властивості
Означення. Функція Іншими словами це означення можна перефразувати: Означення. Функція Означення. Для будь-якого околу Іншими словами: Прообраз при відображенні Приклад. 1. 2. Е = F = R1 3. E = R2 F = Rl Зауваження. В першому означенні використовується метрика, а в означеннях 2, З - тільки відкриті множини і околи. Теорема. Для того, щоб відображення Доведення. Необхідність: нехай відображення Достатність: нехай Зауваження. Теорема справедлива, якщо замінити відкриту множину на замкнену. Зауваження. Прообрази у теоремі не можна заміняти на образ. Наприклад, Теорема. Норма в нормованому векторному просторі Е, яка розглядається як відображення Доведення. Враховуючи нерівність тобто Теорема. Композиція двох неперервних відображень - неперервна. Доведення. Нехай Гомеоморфізми. Означення. Гомеоморфізмом метричного простору Е на метричний простір F називається бієкція Е на F, неперервна разом зі своєю оберненою функцією. Теорема. Для того, щоб бієктивне і неперервне відображення Метричні простори Е і F гомеоморфні, якщо існує хоча б один гомеоморфізм просторів Е і F. У цьому випадку обидва простори мають однакові топологічні властивості, тобто властивості, що стосуються відкритих, замкнених множин та околів. Приклад. Лекція №8.
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 684; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 - замкнена, якщо Ві – замкнені;
- замкнена, якщо Ві – замкнені; - замкнена, якщо Ві – замкнені;
- замкнена, якщо Ві – замкнені;
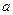
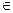 Е називається довільна підмножина Е, яка містить точку
Е називається довільна підмножина Е, яка містить точку  була відкритою необхідно і достатньо, щоб вона була околом кожної своєї точки.
була відкритою необхідно і достатньо, щоб вона була околом кожної своєї точки. підмножини А називається перетин усіх замкнених підмножин Е, які містять А.
підмножини А називається перетин усіх замкнених підмножин Е, які містять А. .
. - відкрита множина. Тоді існує відкрита куля з центром в
- відкрита множина. Тоді існує відкрита куля з центром в  - множина граничних точок множини А.
- множина граничних точок множини А.
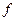 : E
: E  F (E, F - метричні простори з відповідними метриками
F (E, F - метричні простори з відповідними метриками  )
) така, що для будь-якого х
така, що для будь-якого х  випливає, що
випливає, що  .
. точки
точки 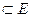 точки
точки  .
.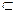 F відкрита множина і
F відкрита множина і  . Якщо
. Якщо  А, то, так як відображення
А, то, так як відображення  - відкрита множина,
- відкрита множина,  окіл
окіл  з природною метрикою, є неперервною функцією.
з природною метрикою, є неперервною функцією. маємо, що
маємо, що  з нерівності
з нерівності  випливає
випливає  ,
, неперервна
неперервна 
 . Нехай
. Нехай  (W) окіл b в F, а так як
(W) окіл b в F, а так як  (V)=
(V)=  випливає неперервність h в
випливає неперервність h в  .
.


