
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Означення та неперервність елементарних функцій.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Як приклад застосування властивостей та теорем доведених у минулих лекціях означимо елементарні функції на Степенева функція. Розглянемо функцію Крім того, функція Отже степенева функція Не складно довести, що функція Крім того, виконуються всі властивості степенів, доведення котрих ми залишаємо для самостійної роботи. Показникова функція. Нехай 1. Якщо Доведення. Оскільки
2. Доведення. Спочатку покажемо, що
Покажемо, що
Оскільки Введемо означення показникової функції для Якщо Означення. Для будь-якого Властивості показникової функції. 1. При
2. Функція Покажемо, що значення Оскільки з нерівності Якщо За теоремою про монотонну функцію, яка заповнює значеннями проміжок, маємо що Якщо Логарифмічна функція. Функція обернена до функції Степенева функція з довільним показником. Нехай
Лекція № 17 Повні простори. Зв'язок повноти і компактності. Ознака Коші. Теорема про нерухому точку. Означення і ознаки повноти. Означення. Нехай в метричному просторі Е задана послідовність
Властивості. 1) Якщо послідовність { 2) Будь-яка послідовність Коші обмежена. 3) Будь-яка підпослідовність послідовності Коші сама є послідовністю Коші. 4) Якщо послідовність Коші має граничну точку, то вона збігається до неї. Означення. Метричний простір Е називається повним, якщо будь-яка послідовність Коші збіжна в даному просторі. Теорема. Будь-який метричний простір Е, усі замкнуті кулі якого компактні, повний. В частинному випадку: повний, будь-який метричний, компактний простір; будь-який скінчено вимірний нормований векторний простір. Доведення. Оскільки кожна послідовність Коші обмежена, то міститься в деякій замкнутій кулі В, тобто в деякому компакті. За теоремою Больцано-Вейєрштрасса вона має граничну точку. Отже, послідовність збігається до цієї граничної точки і простір Е повний. Наприклад. 1. 2. Будь-який метричний простір можна доповнити до повного. Тому, як правило, розглядаються тільки повні простори. 2. Ознаки Коші для границі послідовності і функції в R1. Повнота R1, Rn. Для R1 з попередньої теореми маємо: Теорема (Критерій Коші). Для того, щоб { Аналогічна властивість справедлива в Rn. Критерій Коші для границі функції: Теорема. Нехай
Доведення провести самостійно. Аналогічна властивість справедлива для 3. Теорема про нерухому точку. Означення. Відображення Наприклад: гомотетія з коефіцієнтом k < 1. Легко бачити, стискаюче відображення - рівномірно неперервне відображення. Означення. Точка Теорема. Кожне стискаюче відображення повного метричного простору в себе має нерухому точку, і до того ж єдину. Доведення. Покажемо єдність: нехай Покажемо існування нерухомої точки. Нехай довільна точка
Припустимо, що
Таким чином, {
Зауваження. Оцінка Практичне заняття № 16
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 545; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.153.240 (0.006 с.) |

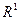 та доведемо їх неперервність.
та доведемо їх неперервність. яка, згідно з властивостями неперервних функцій, неперервна як добуток n неперервних функцій
яка, згідно з властивостями неперервних функцій, неперервна як добуток n неперервних функцій  .
. як композиція неперервних функцій
як композиція неперервних функцій  теж є неперервною на всій множині.
теж є неперервною на всій множині. з раціональним показником
з раціональним показником 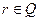 (якщо
(якщо  то
то  і
і  означена вище, якщо
означена вище, якщо  , то
, то  і
і  ) - коректно означена на
) - коректно означена на 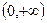 і неперервна на всій множині.
і неперервна на всій множині. строго зростаюча, а
строго зростаюча, а  строго спадаюча.
строго спадаюча. довільне число. Тоді для будь-якого
довільне число. Тоді для будь-якого  і виконуються властивості:
і виконуються властивості:
 , то
, то  .
. для будь-якого
для будь-якого  . Тоді для будь-якого
. Тоді для будь-якого 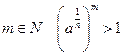 , тобто
, тобто  або
або  для будь-якого
для будь-якого  . Отже
. Отже .
.
 .
. (за нерівністю Бернуллі). Отже
(за нерівністю Бернуллі). Отже  при
при  і з властивості граничних переходів в нерівностях маємо, що
і з властивості граничних переходів в нерівностях маємо, що  при
при  .
. при
при  таке, що
таке, що  при
при 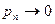 ). Тоді
). Тоді .
. при
при  . Оскільки рівність доведена для будь-якої послідовності
. Оскільки рівність доведена для будь-якої послідовності  ,
,  при
при  .
. такі, що
такі, що 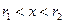 , отже
, отже  . Для будь-яких
. Для будь-яких  і
і  . Таким чином множина
. Таким чином множина  обмежена зверху, а множина
обмежена зверху, а множина  обмежена знизу, отже існують числа
обмежена знизу, отже існують числа  (з означень точної верхньої та нижньої границі). Покажемо, що
(з означень точної верхньої та нижньої границі). Покажемо, що  . За означенням
. За означенням  маємо
маємо  , де
, де 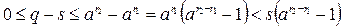 . Оскільки при
. Оскільки при  , маємо:
, маємо:  таке, що якщо
таке, що якщо 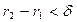 , то
, то  , звідки
, звідки  Таким чином, для будь-якого
Таким чином, для будь-якого  .
. строго зростаюча. Дійсно, якщо
строго зростаюча. Дійсно, якщо  , то існують
, то існують  і
і  та попередньо доведеної властивості 1, маємо
та попередньо доведеної властивості 1, маємо .
. заповнюють множину
заповнюють множину  і
і  Ø.
Ø. , то для
, то для  маємо
маємо  . З аксіоми повноти, існує
. З аксіоми повноти, існує  такий, що
такий, що  для
для  то, оскільки
то, оскільки  при
при  , але з нерівності
, але з нерівності  (у зв’язку з тим, що
(у зв’язку з тим, що  розділяє множини А і В). Однак, за означенням множин А і В, маємо
розділяє множини А і В). Однак, за означенням множин А і В, маємо  Ø, це протирічить вище отриманим включенням. Отже наше припущення невірне, тобто
Ø, це протирічить вище отриманим включенням. Отже наше припущення невірне, тобто  . Аналогічно отримаємо, протиріччя, якщо припустимо
. Аналогічно отримаємо, протиріччя, якщо припустимо  , тобто
, тобто  .
. то
то  , де
, де  і функція
і функція  визначена і неперервна (за властивостями неперервних функцій) та спадаюча на
визначена і неперервна (за властивостями неперервних функцій) та спадаюча на  називається логарифмічною функцією
називається логарифмічною функцією 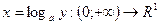 . За теоремою про обернену функцію вона існує та неперервна і монотонна (в залежності від
. За теоремою про обернену функцію вона існує та неперервна і монотонна (в залежності від 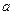 ). З властивостей степенів виконується відповідні властивості логарифмів, які ми залишаємо на самостійне вивчення.
). З властивостей степенів виконується відповідні властивості логарифмів, які ми залишаємо на самостійне вивчення. , тоді степеневою функцією з показником
, тоді степеневою функцією з показником 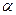 визначимо функцію
визначимо функцію 
 яка існує та неперервна, за теоремою про композицію неперервних функцій.
яка існує та неперервна, за теоремою про композицію неперервних функцій. . Говорять, що це послідовність Коші (фундаментальна), якщо:
. Говорять, що це послідовність Коші (фундаментальна), якщо: (властивість метрична, а не топологічна).
(властивість метрична, а не топологічна). } збіжна, то вона є послідовність Коші.
} збіжна, то вона є послідовність Коші. -повний за теоремою.
-повний за теоремою. - не є повною множиною.
- не є повною множиною. .
.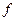 (
( R1, тоді для того, щоб вона мала границю при
R1, тоді для того, щоб вона мала границю при  необхідно і достатньо, щоб
необхідно і достатньо, щоб 

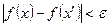
 , де Е - метричний простір, називається стискаючим відображенням, якщо
, де Е - метричний простір, називається стискаючим відображенням, якщо  що для
що для  .
. .
. такі, що
такі, що  - це можливе коли
- це можливе коли  (оскільки k<1)
(оскільки k<1)  .
. . Покладемо
. Покладемо ,…. Покажемо, що {
,…. Покажемо, що {  } - послідовність Коші.
} - послідовність Коші. . Тоді
. Тоді

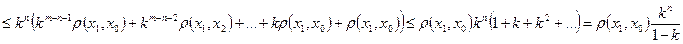 . Отже
. Отже  при
при 
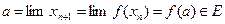 , тобто
, тобто 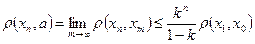 дає швидкість збіжності
дає швидкість збіжності 


