
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: відношення, функції. Дії над функціямиСодержание книги
Поиск на нашем сайте Основні відомості: Означення відношень, функцій. Обернена функція. Композиція функцій. Образ, прообраз. Бієкція. Задачі 1. Відношення, функції. 1.1 Нехай Х=[0, 1] Y=[0, 1]. Побудувати відношення в 1.2 Нехай X=R2, Y=R1. Побудувати функцію в 2. Дії над функціями. Образ, прообраз функції. 2.1 Нехай 1). якщо 2.2 Нехай 1). якщо 2). 2.3 Нехай 2.4 Довести, що якщо 2.5 Найти f(f(x)), якщо 2.6 Знайти Задачі для самостійного розв’язування. 1. Побудувати функціональне відношення в 2. Нехай Х= 3. Довести 4. Довести 5. Побудувати приклад, коли 6. Нехай 7. Довести, що відображення 8. Довести, що відображення 9.Показати, що 10. 11. 12. Навести приклад 14. Навести приклад 16. 18. Лекція №3. Властивості дійсних чисел. Принцип Архімеда. Класи чисел Означення. Множина Приклад. Означення. Множиною натуральних чисел N називається найменша індуктивна множина, що містить 1(1,2,3,...). Принцип математичної індукції. Якщо підмножина Е Означення. Об'єднання множини N, множини чисел, протилежних N і {0} називається множиною цілих чисел Z. Означення. Числа виду Означення. Дійсні числа, які не є раціональними називаються ірраціональними. Загалом отримали: N Алгебраїчне число - корінь рівняння аохn + a1xn-1 +... + аn =0 ai ( Покажемо, що Доведемо, що Розглянемо дві множини X, Y такі, що
І. Покажемо, що s2 = 2. 1) Припустимо, що s2 < 2. Розглянемо s+
Отже 2) Припустимо s2 >2, тоді Залишається єдине – s2 =2. II. Доведемо, що s - ірраціональне. Припустимо, що s - раціональне. Тоді за означенням
Принцип Архімеда. Наслідки. Теорема 1. У будь-якій не порожній підмножині множини N існує максимальний елемент. Доведення. Нехай A Наслідок. Множина N необмежена зверху.
Теорема 2. У будь-якій не порожній обмеженій зверху підмножині множини Z існує максимальний елемент, Доведення. Аналогічно доведенню теореми 1. Наслідок. Множина Z необмежена зверху. Самостійно сформулювати та довести властивості аналогічні теоремам 1,2 для мінімального елемента.
Принцип Архімеда. Нехай х - довільне дійсне число, a h- довільне додатне число. Тоді існує єдине ціле число k, для якого Доведення. Розглянемо множину Наслідки. 1. Доведення. За принципом Архімеда при х=1 і h= 2. Якщо у - довільне дійсне невід'ємне число, і для будь-якого натурального числа n маємо
Доведення. Якщо y>0, то h=y, x=1 одержуємо, що
3. Для будь-яких дійсних чисел а і b таких, що a<b існує число r Доведення. Візьмемо n Практичне заняття №3
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 483; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 , яке не є функцією і функціональним відношенням.
, яке не є функцією і функціональним відношенням. . Довести:
. Довести: ; 2).
; 2).  .
. ;
; .
.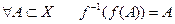 .
. - бієкції, то
- бієкції, то  - бієкція і
- бієкція і  .
. .
. якщо
якщо 
 , в якому будуть використані всі елементи
, в якому будуть використані всі елементи  .
. .
. .
. .
.
 задане співвідношення
задане співвідношення  - бієкція.
- бієкція. відображення
відображення  задане рівняння F(x)=(x, f(x)) –ін’єктивне.
задане рівняння F(x)=(x, f(x)) –ін’єктивне.

 f(x)=ax+b. Знайти
f(x)=ax+b. Знайти  .
. f(x, y)=ax+by+c. Чи має f(x, y) обернену функцію.
f(x, y)=ax+by+c. Чи має f(x, y) обернену функцію. - сюр’єкція 15. Нехай f(x)=ax2+bx+c:
- сюр’єкція 15. Нехай f(x)=ax2+bx+c:  (a>0) – бієкція.
(a>0) – бієкція.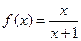 . Знайти f(f(x)). 17.
. Знайти f(f(x)). 17.  . Знайти f
. Знайти f  f(x).
f(x). . Знайти f(f(f(x))).
. Знайти f(f(f(x))).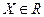 називається індуктивною, якщо
називається індуктивною, якщо 

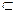 N така, що 1
N така, що 1 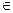 Е і разом з х
Е і разом з х  , m
, m  - трансцендентне число (1882 p.);
- трансцендентне число (1882 p.); 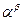 - трансцендентне,
- трансцендентне, 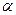 - алгебраїчне,
- алгебраїчне,  - ірраціональне (проблема Гілберта)).
- ірраціональне (проблема Гілберта)). Ø
Ø існує, і
існує, і  ,
, 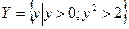 , 1
, 1 
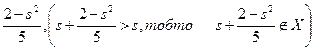 . Відомо, що
. Відомо, що  , розглянемо
, розглянемо де
де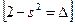 ,
,  .
. , прийшли до суперечності, припущення s2<2 – невірне.
, прийшли до суперечності, припущення s2<2 – невірне.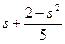 <s. Міркуючи аналогічно як і в попередньому прийдемо до суперечності, тобто припущення s2 > 2 знову невірне.
<s. Міркуючи аналогічно як і в попередньому прийдемо до суперечності, тобто припущення s2 > 2 знову невірне. нескоротний дріб.
нескоротний дріб. - парне число, значить m - парне: m = 2к;
- парне число, значить m - парне: m = 2к;  ;
;  ; 2k2=n2; отже n-парне, n=2p
; 2k2=n2; отже n-парне, n=2p  - скоротний дріб, отже припущення невірне, тобто s - ірраціональне.
- скоротний дріб, отже припущення невірне, тобто s - ірраціональне.
 . Маємо: n =max A, оскільки усі натуральні числа, які більші n, не менші n+1, тобто n+1> c і не містяться у множині А.
. Маємо: n =max A, оскільки усі натуральні числа, які більші n, не менші n+1, тобто n+1> c і не містяться у множині А. .
. - не порожня (оскільки Z - необмежена зверху) обмежена знизу підмножина множини цілих чисел. В ній існує єдиний мінімальний елемент k, тобто
- не порожня (оскільки Z - необмежена зверху) обмежена знизу підмножина множини цілих чисел. В ній існує єдиний мінімальний елемент k, тобто  , тоді
, тоді  .
.
 1<n
1<n  .
. , то у = 0.
, то у = 0. тобто
тобто  , що суперечить даній властивості. Маємо невірне припущення, отже у=0.
, що суперечить даній властивості. Маємо невірне припущення, отже у=0. . Тоді існує k таке, що
. Тоді існує k таке, що  (за принципом Архімеда). При цьому
(за принципом Архімеда). При цьому  , так як в протилежному випадку
, так як в протилежному випадку  і
і  , що суперечить вибору n. Тоді
, що суперечить вибору n. Тоді  буде шуканим, a<r<b.
буде шуканим, a<r<b.


