
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Властивості і ознаки компактності.Содержание книги
Поиск на нашем сайте
Теорема. Для того, щоб топологічний простір Е був компактним, необхідно і достатньо, щоб з будь-якої множини замкнених підмножин Е, перетин яких порожній, можна було вибрати скінченну множину підмножин з порожнім перетином. Доведення. Нехай Наслідок. Якщо простір Е - компактний, а У випадку Е= Теорема. Нехай Е - метричний простір, а F- компактна підмножина Е. Тоді F є замкненою множиною в Е. Доведення. Нехай Зауваження. Замкненість не гарантує компактності. Прикладом є простір R1. Теорема. Будь-яка замкнена підмножина компактного простору є компактним простором. Доведення здійснюється за допомогою необхідної та достатньої умови у термінах замкнених множин. Повернемося до ситуації нормованого простору. Теорема. Для того, щоб підмножина скінченовимірного векторного нормованого простору Е була компактною, необхідно і достатньо, щоб вона була замкненою і обмеженою. Доведення. Необхідність випливає з доведених властивостей в загальній ситуації. Достатність. Припустимо спочатку, що Повторюючи все, що було сказане вище, у випадку простору Е з нормою Теорема Больцано-Вєйерштрасса. Теорема. Для того, щоб метризований простір Е був компактним, необхідно і Доведення. Доведемо необхідність (котру будемо застосовувати нижче). Нехай простір Е компактний і Позначимо Нехай У випадку Е=R1 або Rn теорема звучить наступним чином: Теорема. Больцано-Вєйерштрасса. Із будь-якої обмеженої послідовності в R1 (або Rn) можна виділити збіжну підпослідовність. Це зрозуміло, оскільки обмежена послідовність у R1 (Rn) належить Практичне заняття №14 Тема: Компактні простори Основні відомості: 1.Визначення компактного простору. 2. Необхідні та достатні умови компактності топологічного, метричного та нормованого просторів.. Задачі. 1. Нехай Е компактний простір, а F – замкнена множина в Е. Довести, що F – компактний простір. 2. Довести за допомогою задачі 1, що будь-яка замкнена обмежена множина в R2 компактна. 3. Довести, що об’єднання кінцевого числа компактів є компактом. 4. Показати, що множина 5. Довести, що якщо метричний простір Е – компактен, то з будь-якої послідовності Е можна виділити підпослідовність, що сходиться. Задачі для самостійного розв’язання 1. Довести компактність в R2 множина 2. Довести, що перетин будь-якої сукупності компактів є компактом. 3. Нехай 4. Довести, що відрізок 5. Розглянемо простір 6. Довести, що з будь-якої послідовності точок одиничної окружності в 7. Довести компактність 8. Навести приклад послідовності з якої неможна відокремити підпослідовність, що сходиться, у множині 9. Нехай 1. 2. Довести, що 10. Показати на прикладі, що ствердження задачі 9 не вірне, якщо замінити умову 2 із задачі 9 на: Лекція № 14
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 452; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.2.6 (0.009 с.) |

 замкнені множини такі, що
замкнені множини такі, що  Ø.
Ø.  - відкриті множини. Оскільки
- відкриті множини. Оскільки  - відкрите покриття Е. Тоді компактність Е означає існування скінченого числа
- відкрите покриття Е. Тоді компактність Е означає існування скінченого числа  , таких що
, таких що  =
=  Ø і навпаки.
Ø і навпаки. спадна послідовність замкнених множин Е, перетин яких порожній, то
спадна послідовність замкнених множин Е, перетин яких порожній, то  , що множина
, що множина  - порожня.
- порожня.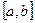 ця властивість називається лемою про вкладені відрізки: Нехай є система вкладених відрізків
ця властивість називається лемою про вкладені відрізки: Нехай є система вкладених відрізків 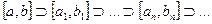 , тоді існує
, тоді існує 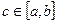 таке, що
таке, що  . Якщо при цьому
. Якщо при цьому  , то таке
, то таке  - єдине.
- єдине.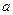 - гранична точка F. Покажемо, що
- гранична точка F. Покажемо, що  Позначимо
Позначимо  , де
, де  — замкнена куля з центром в
— замкнена куля з центром в  Ø. Однак,
Ø. Однак,  , тобто
, тобто  .
. і норма
і норма  . Будь-яка обмежена підмножина міститься в деякій кулі, в нашому випадку замкненому обмеженому паралелепіпеді, тобто міститься в деякому компакті. Оскільки підмножина замкнена, то за попередньою теоремою вона - компактна. Нехай Е - довільний нормований скінченовимірний простір. Обираючи в Е базис
. Будь-яка обмежена підмножина міститься в деякій кулі, в нашому випадку замкненому обмеженому паралелепіпеді, тобто міститься в деякому компакті. Оскільки підмножина замкнена, то за попередньою теоремою вона - компактна. Нехай Е - довільний нормований скінченовимірний простір. Обираючи в Е базис  , одержимо, що
, одержимо, що 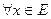 однозначно відповідає точка
однозначно відповідає точка  . Нехай
. Нехай  - норма в Е. Розглянемо в Е норму
- норма в Е. Розглянемо в Е норму  означену вище, вона еквівалентна нормі
означену вище, вона еквівалентна нормі  (див. попередні лекції), отже поняття (замкнений, обмежений, компактний) одні і ті ж для цих норм.
(див. попередні лекції), отже поняття (замкнений, обмежений, компактний) одні і ті ж для цих норм. , маємо, що замкнена і обмежена підмножина Е компактна у топології, що задана нормою
, маємо, що замкнена і обмежена підмножина Е компактна у топології, що задана нормою  .
.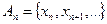 і
і  - його замикання.
- його замикання.  Ø.
Ø. , з іншого боку
, з іншого боку 
 , тобто
, тобто  , значить
, значить  - гранична
- гранична 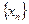 .
. не є компактною в R1.
не є компактною в R1. за допомогою означення.
за допомогою означення. і
і  , причому А і В не порожні, де
, причому А і В не порожні, де  - метричні простори. Довести, що для компактності
- метричні простори. Довести, що для компактності  в
в  з метрикою
з метрикою  , необхідно і достатньо, щоб А і В були компактні.
, необхідно і достатньо, щоб А і В були компактні. , де
, де  довільне, наперед задане число.
довільне, наперед задане число. з нормою
з нормою  . Показати, що в
. Показати, що в  замкнена обмежена множина
замкнена обмежена множина 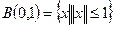 не є компактною.
не є компактною.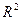 можна виділити підпослідовність, яка сходиться.
можна виділити підпослідовність, яка сходиться. з допомогою теореми Больцано-Вєйерштрасса.
з допомогою теореми Больцано-Вєйерштрасса. .
. послідовність множин в метричному просторі Х таких, що
послідовність множин в метричному просторі Х таких, що - компактна множина для кожного і.
- компактна множина для кожного і. для кожного i >1.
для кожного i >1. Ø.
Ø. для кожного i>1.
для кожного i>1.


