
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Топологічні простори. Еквівалентні метрики і топології.Содержание книги
Поиск на нашем сайте
Еквівалентні метрики і норми, Для означення систем відкритих і замкнених множин, околів, неперервних функцій не обов'язково мати метрику. Все це можна визначити виходячи з систем відкритих множини. Може статися, що дві різні метрики визначають одну і ту ж систему відкритих множин, тоді вони визначають однакові системи замкнених множин, околів і т.д. Наприклад, Означення. Дві метрики у просторі Е називаються еквівалентними, якщо вони визначають одну і ту ж систему відкритих множин (топологію). Це означення можна перефразувати слідуючим чином, тотожне відображення Е (наділене однією метрикою) на Е (наділене другою метрикою) є гомеоморфізмом. У векторному просторі дві норми еквівалентні, якщо еквівалентні відповідні їм метрики. Теорема. Дві норми || ||1 і || ||2 на деякому векторному просторі Е еквівалентні тоді і тільки тоді, коли існують такі додатні сталі k1, k2, що
Доведення. Необхідність. Позначимо через B1(R) (B2 (R)) замкнену кулю з центром в точці 0 радіуса R у розумінні || ||1 (|| ||2). Нехай норми еквівалентні. Тоді В1(1) - окіл 0 одночасно в обох метриках, отже За допомогою гомотетії з коефіцієнтом k2R отримуємо включення Достатність. Якщо умова теореми виконується, то із нерівності ||х||2 Нехай А Наслідок. Усі три норми, визначені вище у Rn - еквівалентні. Довести самостійно. Має місце більш загальне твердження. Теорема. В скінченовимірному векторному просторі над полем дійсних або комплексних чисел будь-які дві норми еквівалентні. Існує єдина система відкритих множин для будь-яких введених у ньому норм. Зауваження. 1. Ця властивість не переноситься на нескінченновимірні векторні простори. 2. Якщо властивість топологічна (тобто залежить від системи відкритих множин, а не від метрики) у нормованому скінченновимірному просторі, то в незалежності від того, яку конкретну норму обрано, вона виконується. Топологічні простори. Існує два види властивостей: метричні, які залежать від метрики; топологічні, що не залежать від метрики, а залежать тільки від системи відкритих і замкнених множин. Зрозуміло, що топологію можна ввести, не використовуючи метрику. Означення. Е називається топологічним простором, якщо в ньому виділено клас підмножин, відкритих у цій топології, які задовольняють властивостям відкритих множин (властивості 1-3 відкритих множин лекція №6). Нижче ми будемо допускати (без додаткових застережень), що система відкритих множин у просторі Е задовольняє також аксіомі Хаусдорфа. Ця вимога завжди буде виконуватися у прикладах, що будуть розглядатися. Приклад. E=R1 відкриті множини – множини, що за допомогою властивостей 1-3 побудовані з будь-яких інтервалів (a, b) Отже, відкрита множина в R1, буде представлятися як об’єднання, не більше ніж зліченної кількості, попарно не перетинаючих інтервалів (довести самостійно або знайти доведення у літературі). Нормовані простори є метричними, а ці – топологічними просторами. Топологічний простір - метризований, якщо існує метрика, що породжує топологію. В основному ми будемо мати справу з метризованими просторами (R1, Rn, функційні простори). Нехай Е - топологічний простір, a F Приклад. Е = R1, F= Зауважимо, що, наприклад, відкрита множина у F -
Практичне заняття № 8 Тема: Елементи топології Необхідні відомості: 1. Визначення метричного і нормованого просторів 2. Визначення відкритих і замкнутих множин і їхньої властивості. 3. Еквівалентність метрик і норм. Задачі 1. Метричні і нормовані простори 1.1 ρ1 (x,y) = arctg│x-y│ на R1 – метрика? 1.2. Чи буде метричним простором сімейство всіх не порожніх підмножин метричного простору Х, якщо відстані між множинами Е 1.3 Нехай Х – множина усіх точок окружності С; приймемо за відстань між точками х є Х і у є Х, візьмемо довжину найкоротшої дуги окружності С, що з'єднує х і у. Чи є ця відстань метрикою? 1.4. Показати, що Rn є векторним простором над полем дійсних чисел. Чи є функція 1.5. Нехай Е - нормований простір. Довести, що 1.6. Привести приклад метрики в R1 не володіє властивостями достатніми для визначення її нормою. 2. Відкриті і замкнуті множини і їхні властивості. Еквівалентні метрики і норми. 2.1. Побудувати ε – куля з центром у точці (0,0) у просторі R2 з метрикою ρ(( 2.2. Чи буде відкритою множина, яка містить кінцеве число точок у просторі R2. 2.3. Довести, що внутрішність множини – відкрита множина. 2.4. Довести властивості відкритих і замкнутих множин. 2.5. Побудувати множину Е, для якої Е' 2.6. Довести, що Е' – завжди замкнуто (для будь-якого Е). 2.7. Нехай на Е задані метрики ρ1 і ρ2. Якщо існують k, k1>0 такі, що для будь-яких х, у є Е виконуються нерівності: ρ1(х,у) ρ2(х,у) то метрики еквівалентні. 2.8. Довести еквівалентність у R3 норм Задачі для самостійного рішення. 1. Нехай Х=R1, ρ (x, y)= sin2(x-y). Чи є (х, ρ) метричним простором? 2. Нехай Х=R1, ρ (x, y)= 3. Нехай Х – довільна не порожня множина ρ (x, y)=1 при 4. Нехай Х – множина усіх прямих на площині, що не проходять через початок координат. Визначите метрику, якщо: l1: x cosα1 + y sin α1 - с1 =0; l2: x cosα2 + y sin α2 - с2 =0; ρ (l1,l2) = Чи буде ρ – метрикою? 5. Нехай у R2 задана 6. Нехай Х- довільний векторний простір. Розглянемо функцію
Чи буде це нормою? 7. Довести, що внутрішність перетинання двох множин дорівнює перетинанню їх внутрощів 8. Нехай Х=[0,1] 9.Нехай Х- простір із задачі 4. Побудувати Вr(х), коли r<1 і r 10. Довести, що внутрішність 11. Довести, що для будь-якого А 12. Привести приклад зліченої множини на площині, що не має граничних точок. 13. Привести приклад зліченої множини на відрізку [0,1] такої, щоб множина її граничних точок збігалася з відрізком [0,1]. 14. Довести, що замкнуте об'єднання двох множин дорівнює об'єднанню їхніх замикань. 15. Довести, що границя 16. Побудувати незлічену множину Е на площині таку, що Е= 17. Привести приклад еквівалентних метрик на площині R2, для яких не виконується мова задачі 2.7.
Послідовності. Лекція №9.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 439; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.39.85 (0.011 с.) |

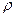 (х,у) і 2
(х,у) і 2  мають місце нерівності:
мають місце нерівності: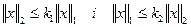
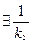 таке, що В1(1)
таке, що В1(1) 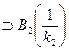 .
. , що означає: з нерівності || х||2
, що означає: з нерівності || х||2  R
R  . Так як перша нерівність справедлива для ||х||2=R, то друга дає при цьому
. Так як перша нерівність справедлива для ||х||2=R, то друга дає при цьому  . Міняючи місцями || ||1 і || ||2 одержимо другу нерівність.
. Міняючи місцями || ||1 і || ||2 одержимо другу нерівність.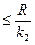 і другої нерівності випливає
і другої нерівності випливає  тобто
тобто 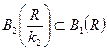 . Звідси випливає, що будь-яка куля у першій метриці заздалегідь містить деяку кулю у другій метриці, і навпаки. За допомогою паралельного перенесення включення переносяться на кулі з довільним центром.
. Звідси випливає, що будь-яка куля у першій метриці заздалегідь містить деяку кулю у другій метриці, і навпаки. За допомогою паралельного перенесення включення переносяться на кулі з довільним центром.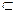 Е відкрита у розумінні метрики 1, тоді
Е відкрита у розумінні метрики 1, тоді  але тоді слідує:
але тоді слідує: 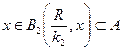 , тобто А - окіл кожної своєї точки у розумінні метрики
, тобто А - окіл кожної своєї точки у розумінні метрики  , тобто відкрита у другій метриці. Аналогічно в обернену сторону, якщо поміняти
, тобто відкрита у другій метриці. Аналогічно в обернену сторону, якщо поміняти 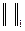 і
і  , відкриті множини в F, це множини побудовані за допомогою властивостей 1-3 з множин виду
, відкриті множини в F, це множини побудовані за допомогою властивостей 1-3 з множин виду 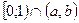 , де (
, де (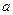 ,b) будь-який інтервал з R1.
,b) будь-який інтервал з R1. , з точки зору Е, не є відкрита множина.
, з точки зору Е, не є відкрита множина.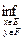 ρ (x,y)?
ρ (x,y)?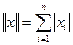 нормою в Rn?
нормою в Rn? для будь-яких х і у.
для будь-яких х і у. ,у), (
,у), (
 Ø, а Е''= Ø.
Ø, а Е''= Ø. ,
, 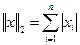 ,
,  .
.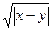 . Чи є (х, ρ) метричним простором?
. Чи є (х, ρ) метричним простором? , ρ (x, y)=0 при х = у. Чи буде (Х, ρ) метричним простором. Чи можна метрику ρ задати нормою?
, ρ (x, y)=0 при х = у. Чи буде (Х, ρ) метричним простором. Чи можна метрику ρ задати нормою? , с1, с2
, с1, с2  .
. Побудувати Вε(0).
Побудувати Вε(0).

 [0,1)
[0,1)  1. Яка множина є околицею точки х є Х.
1. Яка множина є околицею точки х є Х. множини Е є об'єднанням усіх відкритих множин, що містяться в Е.
множини Е є об'єднанням усіх відкритих множин, що містяться в Е. ρ (x,y) <
ρ (x,y) <  , – відкрита.
, – відкрита.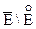 довільної множини Е – завжди замкнута.
довільної множини Е – завжди замкнута.


