Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Границя послідовності та її властивостіСодержание книги
Поиск на нашем сайте Нехай Означення. Послідовність { Якщо Е - нормований простір з нормою Якщо: 1. E = R, означення має вигляд: 2. Е = Rn х=(
Приклад. Доведення. Розглянемо нерівність для якого виконується твердження:
Загальне визначення границі послідовності можна сформулювати в геометричному стилі. Означення. Для будь-якого околу V точки х існує номер N(V), Останнє означення знадобиться коли Е - топологічний простір, але коли Е - метричний простір, то збіжність (існування границі) послідовності - властивість топологічна, а не метрична. Приклад. Нехай E = R1 Властивості границі. Теорема 1. Якщо послідовність має границю у топологічному просторі Е, то вона єдина. Доведення. Припустимо, що Означення. Нехай n1<n2<… будь-яка зростаюча послідовність натуральних чисел. Частину елементів послідовності Теорема 2. Нехай Е - топологічний простір, тоді для того, щоб Доведення слідує з означення границі. (Провести самостійно). Теорема 3. Нехай Е - метризований простір і послідовність Доведення. Нехай Нехай Зауваження. 1. Якщо E=R1, то збіжна послідовність 2. Якщо E=Rn, то обмеженість Теорема 4. Для того, щоб точка Доведення. Достатність. У випадку виконання умови для будь-якого околу V точки Необхідність. Нехай Лекція №10 Послідовності в R1 та в Rn Властивості пов’язані з діями над послідовностями дійсних чисел. Нижче розглянемо властивості числових послідовностей, тобто послідовностей Теорема. Нехай Доведення. Доведемо рівність Маємо:
Отже Доведення інших рівностей провести самостійно. Приклад. Обчислити
Означення. Послідовність Властивості: 1. Скінчена сума нескінченно малих послідовностей — нескінченно мала послідовність. 2. Добуток нескінченно малої послідовності на обмежену послідовність - нескінченно мала послідовність. Означення. Послідовність Властивості. 1. Послідовність, обернена до нескінченно малої є нескінченно велика. 2. Послідовність обернена до нескінченно великої є нескінченно мала. Доведення властивостей нескінченно малих та великих послідовностей слідує з означеної вище властивості та означення границі.
Теорема Вєйєрштрасса про монотонну послідовність. Число е. Теорема. Для того, щоб монотонно зростаюча (спадна) числова послідовність мала скінчену границю необхідно і достатньо, щоб вона була обмежена зверху (знизу). Доведення. Необхідність. Слідує з властивостей послідовностей, що збігаються. Достатність. Нехай зростаюча числова послідовність обмежена зверху, тоді існує 1. 2. Отже: Приклад. Число е. Покажемо, що існує Розглянемо послідовність
(Нерівність За теоремою Вєйєрштрасса існує скінчена границя послідовності
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 469; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 метричний простір. Послідовність в Е, це функція
метричний простір. Послідовність в Е, це функція 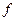 : N→E i
: N→E i  n =
n = 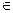 E, яку будемо позначати {
E, яку будемо позначати {  у просторі
у просторі  .
. , то означення має вигляд: послідовність {
, то означення має вигляд: послідовність {  .
. .
. , означення має вигляд: х=
, означення має вигляд: х=  якщо:
якщо: .
. , довести, що
, довести, що  =0.
=0. , тоді
, тоді  , тобто існує
, тобто існує 
 . Отже
. Отже 
 n>N: xn
n>N: xn  .
.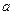 і b. За аксіомою Хаусдорфа
і b. За аксіомою Хаусдорфа  Ø, V i W околи
Ø, V i W околи 
 і
і 

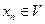 і
і  , що суперечить
, що суперечить 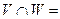 Ø. Таким чином наше припущення невірне.
Ø. Таким чином наше припущення невірне. послідовності
послідовності  .
. (x, x1),...,
(x, x1),...,  ), тоді
), тоді 
 , тобто
, тобто  .
. означає, що існує М, таке що
означає, що існує М, таке що 
 .
. метризованого простору Е була граничною для А, необхідно і достатньо, щоб
метризованого простору Е була граничною для А, необхідно і достатньо, щоб 
 . У ній існує
. У ній існує  . Послідовність
. Послідовність  .
.
 і
і  , тоді
, тоді  - збіжні і
- збіжні і  ,
, 
 =
=  ,
,  =
=  .
. М,
М,  .
.

 .
. =
=  =
= 
 =0:
=0: 
 .
. 
 .
. . З означення
. З означення  виконується властивості:
виконується властивості: .
.
 , тобто виконується означення границі послідовності і
, тобто виконується означення границі послідовності і  . Аналогічно доводиться випадок спадаючої числової послідовності.
. Аналогічно доводиться випадок спадаючої числової послідовності.
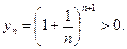 Покажемо, що вона – спадна:
Покажемо, що вона – спадна:
 випливає з нерівності Бернуллі)
випливає з нерівності Бернуллі) . Тоді
. Тоді  - існує. Позначимо
- існує. Позначимо