
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Принцип математичної індукції.Содержание книги
Поиск на нашем сайте Основні відомості: 1. Формули скороченого множення. 2. Принцип математичної індукції. 3. Властивості подільності чисел.
Задачі: 1. Довести тотожність: 1.1. 1.2. Вказівка: помножити 1.3. 2. Довести нерівність: 2.1. 2.2. 3. Довести, що будь-яку суму грошей, більшу 7 копійок, можна обміняти лише трьох копійочними і п’яти копійочними монетами.
Завдання для самостійної роботи. Довести тотожності: 1. 2. 3. 4. 5. 6. Знайти Довести нерівності для 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. Нехай
Довести: 18. Дана послідовність 1. 2. 19. Лекція №4. Кардинальні числа. Означення кардинального числа (потужності множини). Означення. Множини X і Y називаються еквівалентними (X~Y) якщо існує бієкція
Введене відношення Теорема. Нехай при кожному n множини Bn еквівалентні множинам An тоді Доведення. З метою спрощення сприйняття доведення будемо припускати, що множина Bn та An попарно не перетинаються. Нехай
Відношення еквівалентності розбиває сукупність усіх множин на класи еквівалентності. Множини одного класу еквівалентності мають однакову кількість елементів (рівнопотужні), а різних класів - різну кількість. Приклад. 1. Множини точок двох відрізків - рівнопотужні. Взаємно-однозначно співставити елементи цих множин слід так
2. Множини точок півінтервалів Рівнопотужними є множини натуральних чисел і парних натуральних чисел: N~{2n}, n↔2n. Означення. Клас, якому належить множина X називається потужністю множини X або кардинальним числом множини X(card X). Множини одного класу мають однакове кардинальне число, а різних класів -різне. У класі кардинальних чисел існує відношення порядку: якщо Іншими словами: cardX Подібно відношенню порядку на числовій прямій, введене відношення упорядковує потужності, А саме: 1. card X 2. card X 3. Таким чином, клас кардинальних чисел впорядкований. Теорема про множину як завгодно великої потужності. Означення. Потужність X менша за потужність Y (card X < card Y), якщо card X і card X Для будь-якої множини Х. Позначимо P(X)- множину всіх підмножин множини Х. Теорема (Кантор). Потужність не порожньої множини Х менша потужності множини усіх її підмножин: card X < card P (X). Доведення. Оскільки Р(Х) містить одноелементні підмножини, то card X
Тоді: 1. якщо 2. якщо Отримали протиріччя, що й доводить теорему.
Розглянемо найбільш важливі трансфінітні (потужності нескінчених множин) потужності.
Зчисленні множини. Означення. Множина Х називається зчисленною, якщо вона еквівалентна множині натуральних чисел N, тобто card X = card N = а. Теорема (необхідна і достатня умова зчисленності). Для того, щоб множина А була зчисленною необхідно і достатньо, щоб її елементи можна було представити у вигляді послідовності. Доведення. Необхідна умова. Нехай card A=a Достатня умова. Нехай
Приклад 1. Z~N, оскільки
Розглянемо теореми про властивості зчисленних множин. Теорема 1. У будь-якій нескінченій множині можна вибрати зчисленну підмножину. Доведення. Нехай А – нескінченна множина. Візьмемо будь-яке
Теорема 2. Об’єднання скінченної або зчисленної множин – зчисленне. Доведення. Нехай Множину А можливо представити у вигляді
Теорема 3. Декартовий добуток скінченого числа зчисленних множин - зчисленний. Доведення. Нехай А= Нехай при n=k (А= А= Приклад 2 Множина алгебраїчних чисел - зчисленна. Нехай А – множина алгебраїчних чисел, тоді Множина наборів (а0, …, an), аі Приклад 3. card Q=a. Дійсно Теорема 4. Нехай X- нескінчена множина і card А = а, тоді Х Доведення. Оскільки Х – нескінченна, то існує зчисленна множина М
Лекція №5.
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |


 ,
, 
 на
на  .
.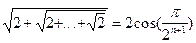 ,
, 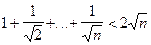 ,
, 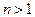
 ,
, 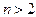



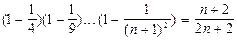
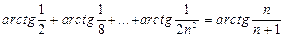


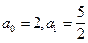
 -й член послідовності.
-й член послідовності.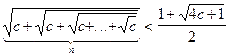 ,
, 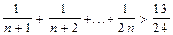
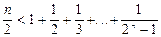
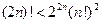
 ,
,  (нерівність Бернуллі)
(нерівність Бернуллі)




 .
.
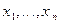 - будь-які невід’ємні числа, при чому
- будь-які невід’ємні числа, при чому  .Довести, що
.Довести, що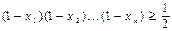
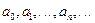
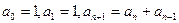 .Довести:
.Довести: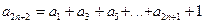
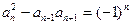
 . Довести, що
. Довести, що 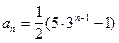
 , (тобто
, (тобто  співставляється елемент у
співставляється елемент у 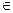 Y, причому різним х співставленні різні у і кожен у
Y, причому різним х співставленні різні у і кожен у  є відношенням еквівалентності (воно задовольняє умовам рефлексивності, симетричності і транзитивності).
є відношенням еквівалентності (воно задовольняє умовам рефлексивності, симетричності і транзитивності). .
. - бієкція і Bn →An, тоді
- бієкція і Bn →An, тоді  , якщо
, якщо 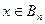 буде бієкцією:
буде бієкцією: 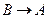 . Тобто В~А.
. Тобто В~А.
 - рівнопотужні. Взаємно-однозначно співставлення елементів цих множин відбувається за допомогою функції y=tg x.
- рівнопотужні. Взаємно-однозначно співставлення елементів цих множин відбувається за допомогою функції y=tg x.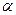 - кардинальне число деякої підмножини множини потужності
- кардинальне число деякої підмножини множини потужності  , то
, то  .
. cardY
cardY 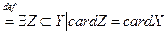 .
. card X
card X  x,
x,  card Y.
card Y. Р(Х). Припустимо супротивне
Р(Х). Припустимо супротивне 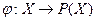 - бієкція. Розглянемо
- бієкція. Розглянемо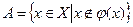 . Оскільки А
. Оскільки А  такий, що
такий, що  (а) =А.
(а) =А. (за означенням А);
(за означенням А); (за означенням А).
(за означенням А). Для будь-якого а
Для будь-якого а  , тобто елемент а розташуємо на n-му місці у послідовності. Таким чином всі елементи множини А розташуються у послідовності.
, тобто елемент а розташуємо на n-му місці у послідовності. Таким чином всі елементи множини А розташуються у послідовності. тоді an↔n, тобто
тоді an↔n, тобто  , бієкція: A→N. Отже A~N, що і доводить теорему.
, бієкція: A→N. Отже A~N, що і доводить теорему.
 і позначимо а1. Оскільки А нескінченна, то у множині А\
і позначимо а1. Оскільки А нескінченна, то у множині А\ 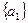 є елементи. Візьмемо будь-який елемент з А\
є елементи. Візьмемо будь-який елемент з А\  є елементи. Продовжуючи процес отримуємо множину
є елементи. Продовжуючи процес отримуємо множину 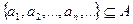 , що й треба довести.
, що й треба довести.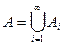 , де card Ai=a, i =1,…. Покажемо, що card A=a, тобто А~N. Оскільки Аі~N то для кожного i =1,… множини Аі можливо представити у вигляді послідовності:
, де card Ai=a, i =1,…. Покажемо, що card A=a, тобто А~N. Оскільки Аі~N то для кожного i =1,… множини Аі можливо представити у вигляді послідовності:  , i =1, 2, ….
, i =1, 2, …. , тоді
, тоді 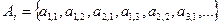 , де розташування елементів у порядку зросту суми індексів. Згідно теореми A~N, що і треба було довести.
, де розташування елементів у порядку зросту суми індексів. Згідно теореми A~N, що і треба було довести. , де Аі – зчисленні. Доведемо по індукції. Нехай n=2
, де Аі – зчисленні. Доведемо по індукції. Нехай n=2  , де
, де  - зчисленна оскільки А1 – зчисленна. Оскільки А2 – зчисленна, то
- зчисленна оскільки А1 – зчисленна. Оскільки А2 – зчисленна, то 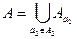 - зчисленне об’єднання зчисленних множин – тобто зчисленна множина, згідно з властивістю 2.
- зчисленне об’єднання зчисленних множин – тобто зчисленна множина, згідно з властивістю 2.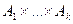 ), А – зчисленна. Доведемо, що при n=k+1 А=
), А – зчисленна. Доведемо, що при n=k+1 А=  - зчисленна. Отже
- зчисленна. Отже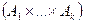
 , множина
, множина  , де Аn множина коренів многочленів порядку n з раціональними коефіцієнтами. Позначимо
, де Аn множина коренів многочленів порядку n з раціональними коефіцієнтами. Позначимо  - множина коренів многочленна а0хn+…+an (вона скінченна), тоді
- множина коренів многочленна а0хn+…+an (вона скінченна), тоді  .
. , і=0,…n зчисленна згідно властивості 3, тобто об’єднання
, і=0,…n зчисленна згідно властивості 3, тобто об’єднання  - зчисленна.
- зчисленна. А ~ X.
А ~ X.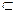 Х, тоді
Х, тоді
 (card A
(card A  , тобто
, тобто 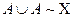 .
.


