
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: повні простори. Ознака Коші. Теорема про нерухому точку.Содержание книги
Поиск на нашем сайте
1. Повні простори. Ознака Коші. 1.1. Довести що збіжна послідовність є послідовністю Коші. 1.2. Послідовність Коші у метричному просторі обмежена. 1.3. Довести повноту 1.4. Довести ознаку Коші для границі функції. 1.5. За ознакою Коші довести, що послідовність збіжна: 1. 2. Теорема про нерухому точку. 2.1. Довести, що стискаюче відображення - рівномірно неперервне. 2.2. Довести, що рівняння 2.3. Довести, що відображення 2.4. Нехай Завдання для самостійної роботи 1. Якщо послідовність Коші має граничну точку, то вона збігається до неї. 2. Розглянемо метричний простір 3. За ознакою Коші довести збіжність послідовності 4. За ознакою Коші довести збіжність послідовності 5. Нехай А і В – повні підпростори метричного простору Х. Довести, що 6. Нехай Х і Y повні метричні простори з метриками 7. Довести, що рівняння 8. Нехай 9. Знайти границю послідовності 10. Довести, що відображення
Лекція №18. Початкові відомості про ряди. Числові ряди. Нехай дана числова послідовність Означення. Символ Позначимо Означення. Границя Приклад. 1. 2. 1-1+1-1+..., Критерій Коші. Ряд
Доведення випливає з ознаки Коші для послідовності. Наслідок 1. Якщо ряд збіжний, то Наслідок 2. Збіжність ряду не залежить від кінцевого числа доданків. Приклад. Гармонічний ряд Дійсно Додатні ряди. Означення. Ряд
Теорема. Для того, щоб додатній ряд був збіжним необхідно і достатньо, щоб послідовність частинних сум була обмежена зверху. Доведення теореми випливає з теореми про границю монотонної послідовності та того, що Теорема порівняння. Нехай Доведення. Позначимо Нехай ряд Ознака Д’аламбера. Нехай Доведення. За умовою Якщо Наслідок. Нехай Якщо q< 1 - ряд збіжний; q>1 – ряд розбіжний. Довести самостійно. Ознака Коші. Нехай Доведення аналогічне доведенню ознаки Д’аламбера. Наслідок. Нехай Якщо q< 1 - ряд збіжний; q>1 – ряд розбіжний. Знакозмінні ряди. Означення. Ряд виду Ознака Лейбніца. Для того, щоб знакозмінний ряд був збіжним достатньо щоб: 1. 2. Доведення. Таким чином за теоремою про монотонну послідовність Наприклад. Ряд Абсолютно збіжні ряди. Означення. Ряд Теорема. Якщо ряд збіжний абсолютно, то він збіжний в звичайному смислі. Доведення. Доведення випливає з ознаки Коші, оскільки виконується Означення. Якщо ряд збіжний, але не збіжний абсолютно, то він називається умовно збіжним. Наприклад. Самостійно розглянути переставну властивість збіжних рядів і добуток за Коші абсолютно збіжних рядів. Практичне заняття № 17
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 365; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.18.73 (0.006 с.) |

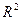 за означенням.
за означенням. 2.
2.  .
. на відрізку
на відрізку  має тільки один корінь.
має тільки один корінь. сжимаюче та знайти точку нерухомості послідовним наближенням.
сжимаюче та знайти точку нерухомості послідовним наближенням. , за теоремою про нерухому точку, довести що існує
, за теоремою про нерухому точку, довести що існує  і знайти його.
і знайти його.
 . Довести, за означенням, що Е не є повним.
. Довести, за означенням, що Е не є повним. .
. .
. - повні.
- повні. і
і  відповідно. Довести, що
відповідно. Довести, що  з метрикою
з метрикою  теж повний простір.
теж повний простір. на відрізку
на відрізку  . Довести за допомогою теореми про нерухому точку, що
. Довести за допомогою теореми про нерухому точку, що  існує і знайти його.
існує і знайти його. (скористатися задачею 9).
(скористатися задачею 9). сжимаюче та знайти точку нерухомості, розв’язуючи відповідну систему рівнянь.
сжимаюче та знайти точку нерухомості, розв’язуючи відповідну систему рівнянь. .
. називається рядом.
називається рядом.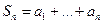 n - частинну суму.
n - частинну суму. послідовності частинних сум називається сумою ряду.
послідовності частинних сум називається сумою ряду.
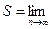
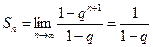 .
. - не існує.
- не існує. збіжний тоді і тільки тоді, коли
збіжний тоді і тільки тоді, коли 

 .
.
 розбігається.
розбігається. отже для
отже для  і
і  критерій Коші не виконується, тобто ряд розбіжний.
критерій Коші не виконується, тобто ряд розбіжний. називається додатнім, якщо
називається додатнім, якщо  .
. - зростаюча.
- зростаюча. додатні ряди. Якщо
додатні ряди. Якщо  , то із збіжності ряду
, то із збіжності ряду 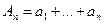 , а
, а  . За умовою теореми
. За умовою теореми  ,
,  . Якщо ряд
. Якщо ряд  - обмежена зверху, тоді і послідовність
- обмежена зверху, тоді і послідовність  - обмежена зверху (за нерівністю) отже, ряд
- обмежена зверху (за нерівністю) отже, ряд  , то ряд збіжний, а якщо
, то ряд збіжний, а якщо 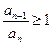 , то ряд розбіжний.
, то ряд розбіжний. . Ряд
. Ряд 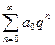 - збіжний (
- збіжний ( ) отже і
) отже і  , то послідовність
, то послідовність  зростаюча і
зростаюча і  , то
, то  , отже ряд
, отже ряд  .
. , то ряд збіжний, а якщо
, то ряд збіжний, а якщо  , то ряд розбіжний.
, то ряд розбіжний. .
. - знакозмінний ряд.
- знакозмінний ряд. ;
;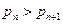 .
. , оскільки
, оскільки  , то
, то  , отже
, отже  - зростаюча послідовність. Крім того,
- зростаюча послідовність. Крім того,  - обмежена зверху.
- обмежена зверху. . Оскільки
. Оскільки 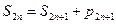 , то
, то  відповідно збігаються до
відповідно збігаються до  – збіжний.
– збіжний. .
.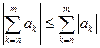 , та ознака Коші для ряду
, та ознака Коші для ряду  .
.


