
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частина 1. Вступ до аналізу.Содержание книги
Поиск на нашем сайте
Лекційно-практичний курс З математичного аналізу. Частина 1. Вступ до аналізу. Зміст Зміст. 2 Передмова. 4 Елементи теорії множин. 5 Лекція №1 Відношення. Функції. 5 Практичне заняття № 1 Тема: Множини. Дії над множинами ………………………… 7 Лекція №2 Відношення порядку. Множина дійсних чисел. Точна верхня (нижня) границя. 8 Практичне заняття № 2 Тема: Відношення, функції. Дії над функціями. 10 Лекція №3 Властивості дійсних чисел. Принцип Архімеда. 11 Практичне заняття №3 Тема: Відношення порядку. Впорядковані множини. Точна верхня і точна нижня грані. Дійсні числа. 13 Практичне заняття № 4 Тема: Верхня та нижня грані множини. Точна нижня та верхня грані. 14 Практичне заняття №5 Тема: Дійсні числа. Формули скороченого множення. Основні нерівності. 16 Практичне заняття №6 Тема: Принцип математичної індукції. 18 Лекція №4. Кардинальні числа. 20 Лекція №5. Множини потужності континуум, та їх властивості. ………………… ……….23 Практичне заняття № 7 Тема: Еквівалентні множини. Зчислені множини. Множини потужності континуум. 25 Елементи топології. 26 Лекція №6 Метричні, нормовані простори. Відкриті, замкнені множини. 26 Лекція №7 Неперервні функції. Гомеоморфізми. 29 Лекція №8. Топологічні простори. Еквівалентні метрики і топології. 31 Практичне заняття № 8 Тема: Елементи топології 33 Послідовності. 35 Лекція №9. Границя послідовності та її властивості 35 Лекція №10. Послідовності в R1 та в Rn 37 Практичне заняття №9. Тема: Границя послідовності. 40 Практичне заняття №10. Тема: Обчислення границі послідовності. Число е. 42 Лекція №11. Границя функції. Означення по Коші і Гейне. Чудові границі. 44 Лекція №12. Властивості границь. Неперервність. Розриви функцій Практичне заняття №11. Тема: Границя функції 50 Практичне заняття №12. Тема: 1а, 2а чудові границі. 52 Практичне заняття №13. Тема: Неперервні функції. Точки розриву функції та їх класифікація. 54 Компактні та зв’язні простори. Властивості неперервних функцій на компактних та зв’язних просторах. 56 Лекція № 13. Компактні простори. Компактні множини в R1 і Rn 56 Практичне заняття №14. Тема: Компактні простори. 59 Лекція № 14. Властивості неперервних функцій на компактних просторах. 60 Лекція № 15. Зв'язні простори. Теорема Больцано-Коші в R1. Існування і неперервність оберненої функції для строго монотонної неперервної функції. 62
Практичне заняття № 15. Тема: Зв’язні множини. Властивості функцій неперервних на відрізку. Рівномірна неперервність. 64 Лекція № 16. Означення та неперервність елементарних функцій. 66 Лекція № 17. Повні простори. Зв'язок повноти і компактності. Ознака Коші. Теорема про нерухому точку. 69 Практичне заняття № 16. Тема: Повні простори. Ознака Коші. Теорема про нерухому точку. 71 Лекція №18. Початкові відомості про ряди. Числові ряди. 72 Практичне заняття № 17. Тема: Числові ряди, їх збіжність. 75 Література. 78
Пропонований посібник призначений для студентів фізико-математичного факультету спеціальності «Математика», а також може використовуватися студентами суміжних спеціальностей, у яких читається курс математичного аналізу. Виклад матеріалу оснований на підході, який використовує елементи топології та функціонального аналізу. Це дозволяє викладати матеріал за принципом: від загального до окремого. Крім того, такий підхід набагато спрощує доведення ряду властивостей, також більш яскраво демонструє причинно-наслідкові зв’язки матеріалу, який викладається. Відзначимо, що для ряду властивостей не наводяться доведення, це стосується тих стверджень, які не важко знайти у загальнодоступній літературі (а також довести самостійно). Протягом всього посібника розташовуються практичні заняття, які, з одного боку, носять тренувальний характер, а з іншого доповнюють викладений теоретичний матеріал. Крім того, відзначимо, що поділ матеріалу на лекції носить умовний характер і зроблений у відповідності з курсом лекцій прочитаних у студентів фізико-математичного факультету. Більш того, студент в кінці знайде список основної літератури по теорії і практиці в сполученні з якими, ми сподіваємося, даний посібник допоможе освоїти предмет більш глибше. Елементи теорії множин. Лекція №1 Відношення. Функції. Властивості. 1). 2). Доведення 1. 1. Нехай
Нехай Доведення 2. (аналогічне доведенню 1)
Означення. Добутком При цьому пари (х, у) і (у, х) з
Образ, прообраз. Композиція Нехай Означення. Образом множини
Множину Властивості: 1. 2. 3. 4. 5.
Доведення провести самостійно.
Нижче будемо використовувати наступну термінологію: 1. f – сюр’єктивне відображення, якщо f(X)=Y 2. f – ін’єктивне відображення, якщо 3. f – бієктивне (взаємно-однозначне) відображення, якщо воно сюр’єктивне і ін’єктивне одночасно. Якщо відображення Відображення Нехай
Практичне заняття № 1 Задачі
1.1. Нехай А, В 1.2 Довести, що А \ В= А 1.3 Довести (В \ С) \ (В \ А) 2. Прямий добуток множин. 2.1 Знайти декартовий добуток множин і описати геометричний образ: а) двох відрізків; б) прямої та окружності; в) побудувати R2, Rn. 2.2. Довести (X 2.3 Довести, що якщо А 3. Відношення. 3.1 Навести приклад відношення, що складається з кінцевого числа елементів. 3.2 Побудувати відношення, яке належить [a,b] Довести
а) прямої і відрізка; б) відрізка й інтервалу; в) двох інтервалів; г) двох прямих. Довести
20. X=[0,1]
Лекція №2. Зростаючі функції. Нехай Е і F - дві впорядковані множини. Означення. Відображення Якщо маємо строгі нерівності, то функція строго зростаюча (спадна). Будемо використовувати ще й наступні терміни: якщо Е впорядкована множина, то [a, b] – замкнений інтервал х: Означення. I. с = sup A, 1. 2. II. с = inf A, 1. 2. Теорема. (про верхню (нижню) границю). Нехай Доведення. Крім множини дійсних чисел R1 ми будемо розглядати простір 1. 2.
3. Приклад. К- кінетична енергія системи n матеріальних частинок залежить від їх швидкостей. Е=К+V – повна енергія – залежить як від конфігурації системи nq, так і від набору швидкостей. Впорядковані пари (q, Практичне заняття № 2 Лекція №3. Класи чисел Означення. Множина Приклад. Означення. Множиною натуральних чисел N називається найменша індуктивна множина, що містить 1(1,2,3,...). Принцип математичної індукції. Якщо підмножина Е Означення. Об'єднання множини N, множини чисел, протилежних N і {0} називається множиною цілих чисел Z. Означення. Числа виду Означення. Дійсні числа, які не є раціональними називаються ірраціональними. Загалом отримали: N Алгебраїчне число - корінь рівняння аохn + a1xn-1 +... + аn =0 ai ( Покажемо, що Доведемо, що Розглянемо дві множини X, Y такі, що
І. Покажемо, що s2 = 2. 1) Припустимо, що s2 < 2. Розглянемо s+
Отже 2) Припустимо s2 >2, тоді Залишається єдине – s2 =2. II. Доведемо, що s - ірраціональне. Припустимо, що s - раціональне. Тоді за означенням
Принцип Архімеда. Наслідки. Теорема 1. У будь-якій не порожній підмножині множини N існує максимальний елемент. Доведення. Нехай A Наслідок. Множина N необмежена зверху.
Теорема 2. У будь-якій не порожній обмеженій зверху підмножині множини Z існує максимальний елемент, Доведення. Аналогічно доведенню теореми 1. Наслідок. Множина Z необмежена зверху.
Самостійно сформулювати та довести властивості аналогічні теоремам 1,2 для мінімального елемента.
Принцип Архімеда. Нехай х - довільне дійсне число, a h- довільне додатне число. Тоді існує єдине ціле число k, для якого Доведення. Розглянемо множину Наслідки. 1. Доведення. За принципом Архімеда при х=1 і h= 2. Якщо у - довільне дійсне невід'ємне число, і для будь-якого натурального числа n маємо
Доведення. Якщо y>0, то h=y, x=1 одержуємо, що
3. Для будь-яких дійсних чисел а і b таких, що a<b існує число r Доведення. Візьмемо n Практичне заняття №3 Практичне заняття № 4 Практичне заняття №5 Практичне заняття №6 Лекція №4. Кардинальні числа. Приклад. 1. Множини точок двох відрізків - рівнопотужні. Взаємно-однозначно співставити елементи цих множин слід так
2. Множини точок півінтервалів Рівнопотужними є множини натуральних чисел і парних натуральних чисел: N~{2n}, n↔2n. Означення. Клас, якому належить множина X називається потужністю множини X або кардинальним числом множини X(card X). Множини одного класу мають однакове кардинальне число, а різних класів -різне. У класі кардинальних чисел існує відношення порядку: якщо Іншими словами: cardX Подібно відношенню порядку на числовій прямій, введене відношення упорядковує потужності, А саме: 1. card X 2. card X 3. Таким чином, клас кардинальних чисел впорядкований. Зчисленні множини. Означення. Множина Х називається зчисленною, якщо вона еквівалентна множині натуральних чисел N, тобто card X = card N = а. Теорема (необхідна і достатня умова зчисленності). Для того, щоб множина А була зчисленною необхідно і достатньо, щоб її елементи можна було представити у вигляді послідовності. Доведення. Необхідна умова. Нехай card A=a Достатня умова. Нехай
Приклад 1. Z~N, оскільки
Розглянемо теореми про властивості зчисленних множин. Теорема 1. У будь-якій нескінченій множині можна вибрати зчисленну підмножину. Доведення. Нехай А – нескінченна множина. Візьмемо будь-яке
Теорема 2. Об’єднання скінченної або зчисленної множин – зчисленне. Доведення. Нехай Множину А можливо представити у вигляді
Теорема 3. Декартовий добуток скінченого числа зчисленних множин - зчисленний. Доведення. Нехай А= Нехай при n=k (А= А= Приклад 2 Множина алгебраїчних чисел - зчисленна. Нехай А – множина алгебраїчних чисел, тоді Множина наборів (а0, …, an), аі Приклад 3. card Q=a. Дійсно Теорема 4. Нехай X- нескінчена множина і card А = а, тоді Х Доведення. Оскільки Х – нескінченна, то існує зчисленна множина М
Лекція №5. Потужність континуума. Теорема. Множина U= Доведення. Припустимо, що U = [0;1] - зчисленна і її елементи можна представити у вигляді послідовності xl,x2,...,xn,.... Розглянемо Числа 0 і 9 не використовуються, так як у противному випадку можливий різний запис числа (0,10200...=0,101999...). Отже, xl,x2,...,хj,... не містить число
Означення. Множини, еквівалентні [0; 1] - множини потужності континуум, нижче це будемо позначати card A=c. Приклад. Враховуючи приклади та властивості з лекції 4 маємо: 1. card 2. card[0;l] = card[0;l) =... = card R = c; 3. Множина трансцендентних чисел нескінчена і має потужність с.
Практичне заняття № 7 Елементи топології. Лекція №6. Приклади. 1. 2. 3. Е – довільна множина, 4. Метрика фізичного простору-часу. Означення. Сферою з центром Означення. Відкритою (замкнутою) кулею з центром Приклади. 1. R: куля – інтервал ( 2. R2: куля – звичайне коло з центром у відповідній точці Означення. Підмножина А Приклад. Множина R і N 2. Нормовані простори. Нехай Е - векторний простір над полем дійсних або комплексних чисел. Означення. Нормою у векторному просторі Е називається будь-яка функція 1. 2. 3. Означення. Якщо у векторному просторі Е задана норма, то Е - нормований векторний простір. Приклади. 1. 3. 5. В інших випадках у метричному просторі відстань не обов'язково задається нормою. В нормованому просторі куля і сфера з центром в Означення. Відрізком з кінцями
Приклад. 1. Довільний інтервал, якщо 2. Якщо E=R2 - прямокутник без границь. 3. Відкриті кулі у довільному метричному просторі Властивості відкритих множин: 1. Множини Е і Ø - відкриті. 2. 3. Доведемо властивість 2. (Доведення 1, 3 самостійно). Нехай 4. Аксіома Хаусдорфа. Для будь-яких Дійсно, А = | |||||||
|
| Поделиться: |

 і
і  ................... 47
................... 47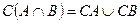

 і
і 
 або В
або В 
 (наприклад)
(наприклад) і звідси маємо, що
і звідси маємо, що  . Таким чином
. Таким чином 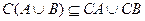 .
. або
або  ,
, 
 . Таким чином
. Таким чином 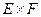 двох множин Е і F називається множина всіх можливих впорядкованих пар (х, у), де
двох множин Е і F називається множина всіх можливих впорядкованих пар (х, у), де  .
. вважаються різними. Аналогічно визначаються
вважаються різними. Аналогічно визначаються  і т.д. Крім того позначимо
і т.д. Крім того позначимо 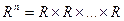 =
=  .
.
 при відображенні
при відображенні  називається множина
називається множина .
. називають прообразом множини
називають прообразом множини  .
.



 ,
, ,
, ,
, 
 , f(х1)=f(x2)
, f(х1)=f(x2)  , таке що: якщо
, таке що: якщо 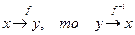 .
.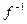 - обернене для
- обернене для 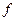 .
. , причому g визначене на f(Х), тоді можна визначити нове відображення
, причому g визначене на f(Х), тоді можна визначити нове відображення  формулою
формулою ,
,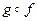 - композиція f і g (g - зовнішнє, а f - внутрішнє відображення).
- композиція f і g (g - зовнішнє, а f - внутрішнє відображення).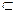 М. Довести еквівалентність включень А
М. Довести еквівалентність включень А  СВ
СВ Y)
Y)  (Z
(Z  (B
(B 
 називається зростаючим, якщо із
називається зростаючим, якщо із  , і відображення
, і відображення  .
. ; (a, b) – відкритий інтервал, a < x < b та ін.
; (a, b) – відкритий інтервал, a < x < b та ін. , якщо:
, якщо:
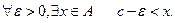


 , В існує оскільки А обмежена. Множини А і В задовольняють аксіому неперервності. Тоді
, В існує оскільки А обмежена. Множини А і В задовольняють аксіому неперервності. Тоді 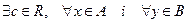 , що
, що 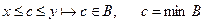 , с – мінімальна верхня границя, тобто с = sup A, причому с – єдине, згідно з раніше доведеним твердженням.
, с – мінімальна верхня границя, тобто с = sup A, причому с – єдине, згідно з раніше доведеним твердженням.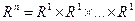 =
=  , а також відображення означенні на цих просторах. Нижче домовимося говорити якщо:
, а також відображення означенні на цих просторах. Нижче домовимося говорити якщо: - функція
- функція  .
. , то маємо дійсну функцію від дійсної змінної.
, то маємо дійсну функцію від дійсної змінної. - то маємо дійсну функцію від n змінних.
- то маємо дійсну функцію від n змінних. ), що відповідають системі, утворюють підмножину Ф в
), що відповідають системі, утворюють підмножину Ф в  , що називається фазовою підмножиною системи частинок.
, що називається фазовою підмножиною системи частинок. 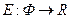 (якщо система замкнена, то Е – const, закон збереження енергії).
(якщо система замкнена, то Е – const, закон збереження енергії).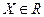 називається індуктивною, якщо
називається індуктивною, якщо 

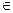 Е і разом з х
Е і разом з х  , m
, m  - трансцендентне число (1882 p.);
- трансцендентне число (1882 p.); 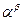 - трансцендентне,
- трансцендентне, 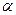 - алгебраїчне,
- алгебраїчне,  - ірраціональне (проблема Гілберта)).
- ірраціональне (проблема Гілберта)). Ø
Ø існує, і
існує, і  ,
, 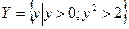 , 1
, 1 
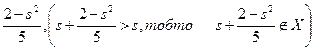 . Відомо, що
. Відомо, що  , розглянемо
, розглянемо де
де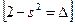 ,
,  .
. , прийшли до суперечності, припущення s2<2 – невірне.
, прийшли до суперечності, припущення s2<2 – невірне.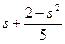 <s. Міркуючи аналогічно як і в попередньому прийдемо до суперечності, тобто припущення s2 > 2 знову невірне.
<s. Міркуючи аналогічно як і в попередньому прийдемо до суперечності, тобто припущення s2 > 2 знову невірне. нескоротний дріб.
нескоротний дріб. - парне число, значить m - парне: m = 2к;
- парне число, значить m - парне: m = 2к;  ;
;  ; 2k2=n2; отже n-парне, n=2p
; 2k2=n2; отже n-парне, n=2p  - скоротний дріб, отже припущення невірне, тобто s - ірраціональне.
- скоротний дріб, отже припущення невірне, тобто s - ірраціональне.
 . Маємо: n =max A, оскільки усі натуральні числа, які більші n, не менші n+1, тобто n+1> c і не містяться у множині А.
. Маємо: n =max A, оскільки усі натуральні числа, які більші n, не менші n+1, тобто n+1> c і не містяться у множині А. .
. - не порожня (оскільки Z - необмежена зверху) обмежена знизу підмножина множини цілих чисел. В ній існує єдиний мінімальний елемент k, тобто
- не порожня (оскільки Z - необмежена зверху) обмежена знизу підмножина множини цілих чисел. В ній існує єдиний мінімальний елемент k, тобто  , тоді
, тоді  .
.
 1<n
1<n  .
. , то у = 0.
, то у = 0. тобто
тобто  , що суперечить даній властивості. Маємо невірне припущення, отже у=0.
, що суперечить даній властивості. Маємо невірне припущення, отже у=0. . Тоді існує k таке, що
. Тоді існує k таке, що  (за принципом Архімеда). При цьому
(за принципом Архімеда). При цьому  , так як в протилежному випадку
, так як в протилежному випадку  і
і  , що суперечить вибору n. Тоді
, що суперечить вибору n. Тоді  буде шуканим, a<r<b.
буде шуканим, a<r<b.
 - рівнопотужні. Взаємно-однозначно співставлення елементів цих множин відбувається за допомогою функції y=tg x.
- рівнопотужні. Взаємно-однозначно співставлення елементів цих множин відбувається за допомогою функції y=tg x. .
. cardY
cardY 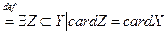 .
. x,
x,  Для будь-якого а
Для будь-якого а  , тобто елемент а розташуємо на n-му місці у послідовності. Таким чином всі елементи множини А розташуються у послідовності.
, тобто елемент а розташуємо на n-му місці у послідовності. Таким чином всі елементи множини А розташуються у послідовності. тоді an↔n, тобто
тоді an↔n, тобто  , бієкція: A→N. Отже A~N, що і доводить теорему.
, бієкція: A→N. Отже A~N, що і доводить теорему.
 і позначимо а1. Оскільки А нескінченна, то у множині А\
і позначимо а1. Оскільки А нескінченна, то у множині А\ 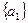 є елементи. Візьмемо будь-який елемент з А\
є елементи. Візьмемо будь-який елемент з А\  є елементи. Продовжуючи процес отримуємо множину
є елементи. Продовжуючи процес отримуємо множину 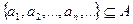 , що й треба довести.
, що й треба довести.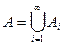 , де card Ai=a, i =1,…. Покажемо, що card A=a, тобто А~N. Оскільки Аі~N то для кожного i =1,… множини Аі можливо представити у вигляді послідовності:
, де card Ai=a, i =1,…. Покажемо, що card A=a, тобто А~N. Оскільки Аі~N то для кожного i =1,… множини Аі можливо представити у вигляді послідовності:  , i =1, 2, ….
, i =1, 2, …. , тоді
, тоді 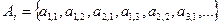 , де розташування елементів у порядку зросту суми індексів. Згідно теореми A~N, що і треба було довести.
, де розташування елементів у порядку зросту суми індексів. Згідно теореми A~N, що і треба було довести. , де Аі – зчисленні. Доведемо по індукції. Нехай n=2
, де Аі – зчисленні. Доведемо по індукції. Нехай n=2  , де
, де  - зчисленна оскільки А1 – зчисленна. Оскільки А2 – зчисленна, то
- зчисленна оскільки А1 – зчисленна. Оскільки А2 – зчисленна, то 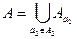 - зчисленне об’єднання зчисленних множин – тобто зчисленна множина, згідно з властивістю 2.
- зчисленне об’єднання зчисленних множин – тобто зчисленна множина, згідно з властивістю 2.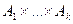 ), А – зчисленна. Доведемо, що при n=k+1 А=
), А – зчисленна. Доведемо, що при n=k+1 А=  - зчисленна. Отже
- зчисленна. Отже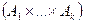
 , множина
, множина  , де Аn множина коренів многочленів порядку n з раціональними коефіцієнтами. Позначимо
, де Аn множина коренів многочленів порядку n з раціональними коефіцієнтами. Позначимо  - множина коренів многочленна а0хn+…+an (вона скінченна), тоді
- множина коренів многочленна а0хn+…+an (вона скінченна), тоді  .
. , і=0,…n зчисленна згідно властивості 3, тобто об’єднання
, і=0,…n зчисленна згідно властивості 3, тобто об’єднання  - зчисленна.
- зчисленна.
 (card A
(card A  , тобто
, тобто 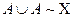 .
.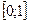 не еквівалентна множині натуральних чисел N.
не еквівалентна множині натуральних чисел N. ,
,  виберемо довільне ціле число від 1 до 8 включно, відмінне від j–го десяткового знака числа хj. Таким чином, що
виберемо довільне ціле число від 1 до 8 включно, відмінне від j–го десяткового знака числа хj. Таким чином, що  - десятковий дріб відмінний від хn,(так як n-й знак відмінний від 0,9 і n-го знака хn).
- десятковий дріб відмінний від хn,(так як n-й знак відмінний від 0,9 і n-го знака хn). , це протиріччя свідчить, що наше припущення невірно, тобто U
, це протиріччя свідчить, що наше припущення невірно, тобто U  N
N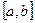 = c;
= c;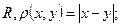
 - евклідова метрика, або природня метрика (приклад 1 маємо при
- евклідова метрика, або природня метрика (приклад 1 маємо при 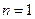 );
);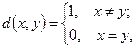 (дискретна метрика);
(дискретна метрика);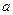 радіуса R > 0 називається множина
радіуса R > 0 називається множина 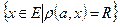
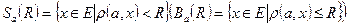
 Е метричного простору (Е,
Е метричного простору (Е, 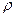 ) називається обмеженою, якщо існує куля в якій вона міститься.
) називається обмеженою, якщо існує куля в якій вона міститься. обмежені.
обмежені.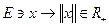 , для якої виконуються умови:
, для якої виконуються умови: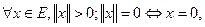
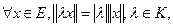
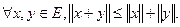
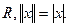 2.
2.  .
.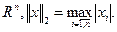 4.
4. 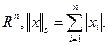
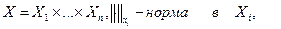
 Якщо Е - нормований простір, то в ньому можна визначити відстань
Якщо Е - нормований простір, то в ньому можна визначити відстань 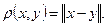 Де
Де 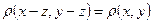 і
і  . Навпаки, якщо
. Навпаки, якщо 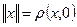 . (Довести самостійно)
. (Довести самостійно)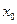 мають вигляд
мають вигляд 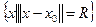 і
і 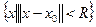 .
.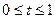 і позначають
і позначають  .
.
 - відкрите, якщо Aі відкриті.
- відкрите, якщо Aі відкриті. - відкрите, якщо Аі відкриті.
- відкрите, якщо Аі відкриті. тоді
тоді 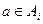 для всіх і=1,…, n. При кожному і
для всіх і=1,…, n. При кожному і  Отже
Отже 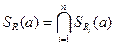 - куля з центром
- куля з центром 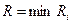 і
і 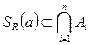 . Таким чином оскільки
. Таким чином оскільки 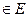 існує дві відкриті непересічні підмножини А, В
існує дві відкриті непересічні підмножини А, В 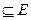 , що включають
, що включають 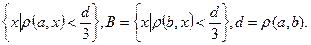 А, В - відкриті і не мають спільних точок, в протилежному випадку, якщо
А, В - відкриті і не мають спільних точок, в протилежному випадку, якщо 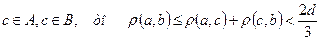 , що невірно.
, що невірно.


