
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: 1а, 2а чудові границі.Содержание книги
Поиск на нашем сайте
Основні відомості: Види 1-ї та 2-ї чудових границь. Задачі: Обчислити, використовуючи першу чудову границю: 1.1. 1.2. 1.3. 1.4. 1.5. Обчислити, використовуючи другу чудову границю: 2.1. 2.2. 2.3. 2.4. Обчислити за допомогою полярних та сферичних координат 3.1. 3.2. 3.3. Завдання для самостійної роботи. 1. 3. 5. 7. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. Практичне заняття №13 Тема: Неперервні функції. Точки розриву функції та їх класифікація. Основні відомості: 1.Визначення неперервності функції в точці. 2.Властивості неперервної функції в точці. 3.Розриви. 4. Класифікація розривів. Задачі 1.1.Довести неперервність в кожній точці за означенням: 1.2.Функція 1.3.Довести, що якщо функція. Дослідити на неперервність та зобразити графічно і з'ясувати характер розриву. 2.1. 2.2. 2.3. Довести, що функція 2.4. 2.5. Завдання для самостійної роботи. Довести неперервність в кожній точці за означенням. 1. y=2x-1 2. y= 3. 4. y=x3 5. y=cosx 6. Нехай 7. 8. 9. 10. 11. 12. 13. Чи існує 14. 15. 16. Чи існують 17. 18. 19. 20. Функція 21.Довести, що якщо у = 22.Нехай 23.Нехай
24.Чи можливо стверджувати, що квадрат розривної функції є також розривна функція. 25.Довести, що якщо функція монотонна, то будь-яка її точка розриву є точка розриву 26. 27. Компактні та зв’язні простори. Властивості неперервних функцій на компактних та зв’язних просторах. Лекція № 13 Компактні простори. Компактні множини в R1 і Rn Означення компактних просторів. Приклади. Нехай Е - топологічний простір. Означення. Множина підмножин Е називається покриттям Е, якщо будь-яка точка x з Е належить хоча б одній з цих підмножин. Покриття скінчене - якщо воно складається з скінченого числа множин. Покриття відкрите - якщо воно складається з відкритих множин. Наприклад Означення. Підпокриттям називається покриття, утворене з множин першого покриття. Означення (властивість Гейне-Бореля-Лебега). Топологічний простір називається компактним, якщо з будь-якого його відкритого покриття можна виділити хоча б одне скінчене підпокриття. Зауваження. Компактність - властивість простору Е. Можливо розглядати компактність Приклади. 1. Простір, що містить скінчене число точок - компактний. 2. R1, R2, векторні нормовані простори - не компактні, так як множина відкритих куль з центром в точці 0 і радіусом більше нуля утворює відкрите покриття. Будь-яке скінчене число цих куль міститься в одній кулі скінченого радіуса і, отже, не покриває всього простору. В загальному вигляді, будь-яка необмежена підмножина метричного простору не компактна. Необхідна умова компактності метричного простору - обмеженість. Теорема. Будь-який відрізок Доведення. Нехай Припустимо, що з
Так як Теорема. В Rn замкнений обмежений паралелепіпед, тобто множина Довести аналогічно доведенню попередньої теореми.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 365; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.189.119 (0.009 с.) |













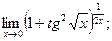




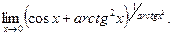


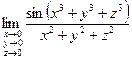
 2.
2. 
 4.
4. 
 6.
6. 
 8.
8. 






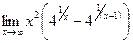
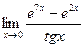









 27.
27.  28.
28. 
 .
.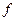 (х) неперервна в точці х0 та в будь-якому околі цієї точки є як значення х, в яких функція додатня, так і значення x, в яких функція від'ємна. Знайти
(х) неперервна в точці х0 та в будь-якому околі цієї точки є як значення х, в яких функція додатня, так і значення x, в яких функція від'ємна. Знайти  є також неперервна
є також неперервна


 та розривна в інших точках.
та розривна в інших точках.


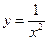
 0. Довести, що існує число c>0 і окіл точки х0 такі, що для будь-якого x з цього околу справедлива нерівність
0. Довести, що існує число c>0 і окіл точки х0 такі, що для будь-якого x з цього околу справедлива нерівність  . Визначити точки розриву функцій та дослідити характер цих точок.
. Визначити точки розриву функцій та дослідити характер цих точок.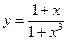






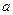 при якому функція
при якому функція 


 при яких
при яких 
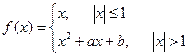


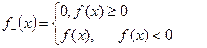 неперервні на Х.
неперервні на Х.
 28.
28. 
 відкрите покриття R1
відкрите покриття R1 з індукованою в
з індукованою в  топологією при цьому Е може бути не компактним простором.
топологією при цьому Е може бути не компактним простором. - компактна множина.
- компактна множина. відкрите покриття
відкрите покриття 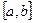 і с - середина
і с - середина  ]. Розділивши його на два, ми одержали [
]. Розділивши його на два, ми одержали [  ], що має ті ж властивості. Таким чином, отримали послідовність [
], що має ті ж властивості. Таким чином, отримали послідовність [  ],... під інтервалів
],... під інтервалів  - зростає і обмежена зверху, тоді
- зростає і обмежена зверху, тоді 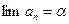 .
. - спадає і обмежена знизу, тоді
- спадає і обмежена знизу, тоді  .
. при
при  , то
, то  Тоді будь-який відкритий інтервал, що містить
Тоді будь-який відкритий інтервал, що містить 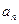 i
i 
 , а значить, містить і всі [
, а значить, містить і всі [  і для достатньо великих n
і для достатньо великих n  . Прийшли до суперечності з тим, що [
. Прийшли до суперечності з тим, що [  є компактним простором.
є компактним простором.


