
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачі для самостійного рішенняСодержание книги
Поиск на нашем сайте 1. Установити взаємно – однозначна відповідність між N і множиною чисел, які поділяються на 3 із залишком 2. 2. Установити взаємно – однозначна відповідність між крапками концентричних окружностей. 3. Установити взаємно – однозначна відповідність між сферою з виколотим полюсом і площиною. 4. Побудувати взаємно – однозначна відповідність окружності одиничного радіуса на відрізок [0,1]. 5. Установити взаємно – однозначну відповідність між відкритим одиничним колом і замкнутим одиничним колом. 6. Знайти взаємно – однозначну відповідність між замкнутим одиничним колом і доповненням до відкритого одиничного кола. 7. Довести, що множина кіл площини з раціональними радіусами і координатами центра – зліченна. 8. Довести, що множина непересічних трикутників площини – зліченна. 9. Довести, що якщо відстань між будь-якими двома крапками множини Е на прямої більше 1, то множина Е кінцева чи зліченна. 10. Нехай Е зліченна множина на 11. Довести, що множина дробова – раціональних функцій 12. Довести, що довільний замкнутий квадрат на площині має потужність континуума. 13. Довести, що множина усіх кінцевих підмножин зліченної множини – зліченна. А множина усіх підмножин зліченної множини має потужність континуума. 14. Яка потужність множини всіх кінцевих послідовностей дійсних чисел. 15. Яка потужність усіх відрізків на числовій прямій? 16. Яка потужність множини всіх кіл на площині? 17. Яка потужність усіх правильних багатокутників на площині? 18. Довести, що множина дробово–раціональних функцій (див. задачу 11) з дійсними коефіцієнтами має потужність континуум. 19. Яка потужність множини всіх послідовностей дійсних чисел. 20. Довести, що множина усіх числових функцій, визначених на [ a,b ] має потужність гіперконтинуума. Елементи топології. Лекція №6. Метричні, нормовані простори. Відкриті, замкнені множини. Метричні простори. Приклади. Шар. Сфера. Означення. На множині Е задана метрика
1. 2. 3. Пара Приклади. 1. 2. 3. Е – довільна множина, 4. Метрика фізичного простору-часу. Означення. Сферою з центром Означення. Відкритою (замкнутою) кулею з центром Приклади. 1. R: куля – інтервал ( 2. R2: куля – звичайне коло з центром у відповідній точці Означення. Підмножина А Приклад. Множина R і N 2. Нормовані простори. Нехай Е - векторний простір над полем дійсних або комплексних чисел. Означення. Нормою у векторному просторі Е називається будь-яка функція 1. 2. 3. Означення. Якщо у векторному просторі Е задана норма, то Е - нормований векторний простір. Приклади. 1. 3. 5. В інших випадках у метричному просторі відстань не обов'язково задається нормою. В нормованому просторі куля і сфера з центром в Означення. Відрізком з кінцями
Відкриті, замкнені множини. Замикання. Означення. Підмножина А метричного простору Приклад. 1. Довільний інтервал, якщо 2. Якщо E=R2 - прямокутник без границь. 3. Відкриті кулі у довільному метричному просторі Властивості відкритих множин: 1. Множини Е і Ø - відкриті. 2. 3. Доведемо властивість 2. (Доведення 1, 3 самостійно). Нехай 4. Аксіома Хаусдорфа. Для будь-яких Дійсно, А = Означення. Множина В - замкнена в Е, якщо Е \ В = СВ — відкрита. Приклади. 1. 2. 3. Замкнена куля у довільному метричному просторі. 4. Скінчена кількість точок у довільному метричному просторі.
|
||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 481; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

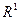 . Чи можна зрушити цю множину на величину а (тобто замінити всі крапки х
. Чи можна зрушити цю множину на величину а (тобто замінити всі крапки х 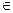 Е на х + а) так, щоб отримана множина Еа не перетиналася з Е?
Е на х + а) так, щоб отримана множина Еа не перетиналася з Е? , де
, де 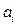 ,b,
,b, 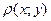 : якщо визначена функція
: якщо визначена функція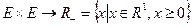 і виконуються умови:
і виконуються умови: ,
, 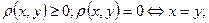

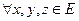

 називається метричним простором.
називається метричним простором.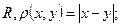
 - евклідова метрика, або природня метрика (приклад 1 маємо при
- евклідова метрика, або природня метрика (приклад 1 маємо при 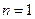 );
);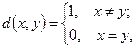 (дискретна метрика);
(дискретна метрика);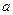 радіуса R > 0 називається множина
радіуса R > 0 називається множина 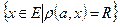
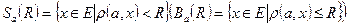
 Е метричного простору (Е,
Е метричного простору (Е, 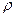 ) називається обмеженою, якщо існує куля в якій вона міститься.
) називається обмеженою, якщо існує куля в якій вона міститься. обмежені.
обмежені.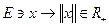 , для якої виконуються умови:
, для якої виконуються умови: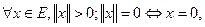
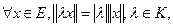
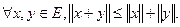
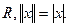 2.
2.  .
.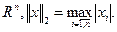 4.
4. 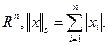
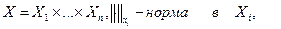
 Якщо Е - нормований простір, то в ньому можна визначити відстань
Якщо Е - нормований простір, то в ньому можна визначити відстань 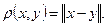 Де
Де 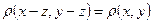 і
і  . Навпаки, якщо
. Навпаки, якщо 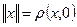 . (Довести самостійно)
. (Довести самостійно)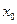 мають вигляд
мають вигляд 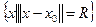 і
і 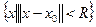 .
.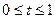 і позначають
і позначають 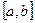 .
. .
. - відкрите, якщо Aі відкриті.
- відкрите, якщо Aі відкриті. - відкрите, якщо Аі відкриті.
- відкрите, якщо Аі відкриті. тоді
тоді 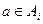 для всіх і=1,…, n. При кожному і
для всіх і=1,…, n. При кожному і  Отже
Отже 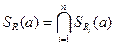 - куля з центром
- куля з центром 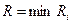 і
і 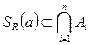 . Таким чином оскільки
. Таким чином оскільки 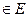 існує дві відкриті непересічні підмножини А, В
існує дві відкриті непересічні підмножини А, В 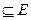 , що включають
, що включають 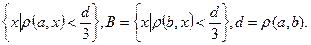 А, В - відкриті і не мають спільних точок, в протилежному випадку, якщо
А, В - відкриті і не мають спільних точок, в протилежному випадку, якщо 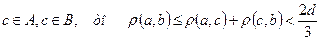 , що невірно.
, що невірно. .
.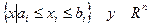 .
.


