
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Означення. Неперервні відображення зв'язаних просторів.Содержание книги
Поиск на нашем сайте
Простори можуть становити дещо ціле (куля, Rn), а можуть складатися з декількох частин (об’єднання двох сфер). В зв’язку з цим домовимося про деяку термінологію. Означення. Топологічний простір називається зв'язаним, якщо його не можна розбити на дві відкриті (замкнуті) підмножини, які не перетинаються, або якщо в Е не існує одночасно відкритої і замкненої множини крім Е та Ø. Теорема. Для того, щоб підмножина Доведення. Необхідність. Нехай Е - зв'язна підмножина R1, а Достатність випливає з означення. Наслідок. Множина Q - не зв'язна. Теорема. Образ зв'язного топологічного простору при неперервному відображені є зв'язним. Доведення. Нехай Якщо б
Наслідок. Якщо неперервна функція Таким чином виконуються теореми: Теорема (Больцано-Коші) 1. Нехай функція Теорема (Больцано-Коші) 2. Нехай функція Властивість проміжних значень ( необхідна умова неперервності функції на відрізку Неперервна на відрізку Приклад того, що ця умова не є достатньою: функція
Теорема про обернену функцію Властивість проміжних значень для монотонних функцій є достатньою умовою для неперервності. Теорема. Нехай Доведення. Рівність Покажемо, що Нехай Покажемо, що необхідна умова неперервності функції на відрізку, для строго монотонної функції, буде і достатньою умовою. Теорема. Нехай Доведення. Припустимо, що Тоді відрізок Приклади. 1. Функція 2. Функція 3. Функція, обернена до функції з приклада 1 Практичне заняття № 15 Тема: Зв’язні множини. Властивості функцій неперервних на відрізку. Рівномірна неперервність. Основні відомості. Зв’язні множини.Теореми Вейерштрасса, Больцано-Коші, Кантора, теорема про неперервність оберненої функції та їх наслідки. Задачі. Зв’язні множини. 1.1. Довести, за означенням, що множина 1.2. Довести, що множина 1.3. Довести, що об’єднання двох зв’язних множин Е1, Е2 є множина зв’язна, якщо Властивості неперервних функцій. 2.1. Довести, що якщо функція 2.2. Нехай функція визначена та монотонна на проміжку і множина її значень - проміжок. Довести, що ця функція неперервна. 2.3.Функції 2.4 Функція 2.5. 3найти всі неперервні на R функції Рівномірна неперервність. 3.1.Довести рівномірну неперервність функції 3.2. Довести, що сума скінченої кількості рівномірно неперервних на інтервалі 3.3. Довести, що якщо обмежена монотонна функція Завдання для самостійної роботи. 1. Функція 2. Довести, що якщо функція визначена та неперервна на проміжку, то множина її значень проміжок (тобто відрізок, або інтервал, або напівінтервал). Вказівка: застосуйте теорему про проміжне значення. 3. Нехай функція, визначена на відрізку функція строго монотонна на Вказівка: показати, що максимум та мінімум функція має на кінцях відрізку (із зворотності). 4. Довести, що рівняння 5. Довести, що будь-який многочлен непарного ступеню має хоча б один дійсний корінь. 6. Довести, що якщо многочлен парного ступеню приймає хоча б одно значення, протилежне по знаку коефіцієнту старшого члену, то він має не менш як два дійсні корні. 7. Довести, що якщо функція
Вказівка: використати теорему про проміжне значення. 8. Нехай функція 9. Неперервні функції Вказівка: розглянути функцію 10. Функція Вказівка: показати що ствердження 11. Функція Довести, що для будь-якого 12. Знайти всі неперервні на R функції, задовольняючі для будь-яких 13. Знайти всі неперервні на 14. Знайти всі неперервні на 15. Довести, що якщо
Довести рівномірну неперервність функцій: 16. Вказівка: використати задачу 3.3. 17. 18. Довести, що у = sin 19 Довести, що у = 20.Довести, що якщо функція рівномірно неперервна на проміжку, то вона неперервна на 21. Довести, що якщо функція задовольняє умові Ліпшица на Х, то вона на X рівномірно 22. Довести, що якщо функція необмежена на обмеженому інтервалі, то вона не є рівномірно неперервною на цьому інтервалі. 23. Довести, що якщо функція 24. Довести, що якщо 25. Довести, що обмежена, монотонна, неперервна на інтервалі функція рівномірно 26. Навести приклад двох зв’язних множин, перетин яких не є зв’язна множина. 27. Довести, що множина з 28. Довести, що якщо Е – зв’язна, то 29. Довести, що відрізок, який з’єднує дві точки площини тривимірного евклідового простору – зв’язна множина. 30. Довести, що множина точок площини, у яких хоча б одна координата раціональна, зв’язна. Лекція № 16
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 447; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.250.115 (0.009 с.) |

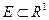 була зв'язним топологічним простором, необхідно і достатньо, щоб вона була відкритим, напіввідкритим, або замкненим інтервалом (можливо і нескінченним).
була зв'язним топологічним простором, необхідно і достатньо, щоб вона була відкритим, напіввідкритим, або замкненим інтервалом (можливо і нескінченним).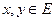 . Покажемо, що
. Покажемо, що 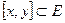 . Якщо це не так, тo
. Якщо це не так, тo 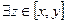 і
і  . Тоді відкриті множини
. Тоді відкриті множини  та
та  перетинаються з Е, ділять Е на дві відкриті множини, які не перетинаються. Отже, множина Е - не зв'язна. Якщо
перетинаються з Е, ділять Е на дві відкриті множини, які не перетинаються. Отже, множина Е - не зв'язна. Якщо 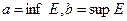 , то Е співпадає з
, то Е співпадає з 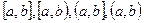 (де
(де  можливо і нескінченні).
можливо і нескінченні).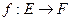 ,
, 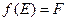 . Покажемо зв'язність F.
. Покажемо зв'язність F. було незв'язним, то
було незв'язним, то 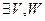 - відкриті.
- відкриті. 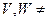 Ø.
Ø. 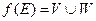 і
і 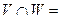 Ø
Ø 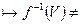 Ø,
Ø, 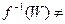 Ø – відкриті,
Ø – відкриті,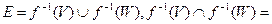 Ø
Ø  - незв'язаний простір, що й доводить теорему.
- незв'язаний простір, що й доводить теорему.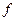 визначена на зв'язному просторі Е, із значеннями в R1, то множина її значень є відкритим, напіввідкритим або замкнутим інтервалом в R1.
визначена на зв'язному просторі Е, із значеннями в R1, то множина її значень є відкритим, напіввідкритим або замкнутим інтервалом в R1.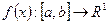 і неперервна на
і неперервна на 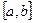 та
та  , то
, то 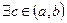 , що
, що 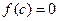 .
. , тоді
, тоді 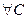 між А і В
між А і В  .
.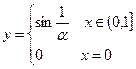 має розрив у
має розрив у  2-го роду, але значеннями заповнює відрізок
2-го роду, але значеннями заповнює відрізок 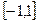 .
.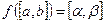 , а
, а  . Причому обернена функція строго зростаюча (спадаюча).
. Причому обернена функція строго зростаюча (спадаюча).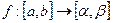 - сюр’єктивно. Оскільки
- сюр’єктивно. Оскільки 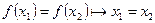 , тобто
, тобто 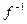 - строго зростаюча.
- строго зростаюча.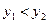 , де
, де  , тоді
, тоді 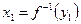
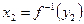 , якщо припустити, що
, якщо припустити, що 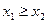 то згідно з умовою теореми
то згідно з умовою теореми  , отже
, отже 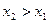 , тобто функція
, тобто функція  строго зростаюча.
строго зростаюча.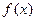 неперервна на
неперервна на 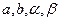 - можуть бути і нескінченними).
- можуть бути і нескінченними).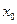 точка розриву зліва, маємо
точка розриву зліва, маємо  (для
(для  при
при  , отже
, отже 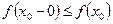 , але оскільки в
, але оскільки в 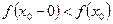 ).
). не заповнюється повністю значеннями функції
не заповнюється повністю значеннями функції 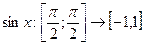 неперервна згідно з останньою теоремою, оскільки строго зростаюча.
неперервна згідно з останньою теоремою, оскільки строго зростаюча.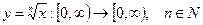 - обернена до функції
- обернена до функції  . Оскільки
. Оскільки  - строго зростаюча і неперервна (згідно властивостям неперервних функцій), то згідно теоремі про обернену функцію
- строго зростаюча і неперервна (згідно властивостям неперервних функцій), то згідно теоремі про обернену функцію  неперервна.
неперервна.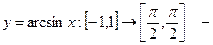 неперервна, згідно прикладу 1 і теоремі про обернену функцію.
неперервна, згідно прикладу 1 і теоремі про обернену функцію. не буде зв’язною.
не буде зв’язною. зв’язна.
зв’язна. Ø
Ø неперервна в
неперервна в 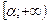 та існує скінчений
та існує скінчений 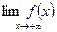 то ця функція обмежена на даному проміжку.
то ця функція обмежена на даному проміжку.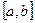 та
та 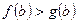 і
і  . Довести, що існує
. Довести, що існує 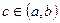 така, що
така, що 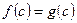 .
.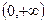 , та не має границі при
, та не має границі при 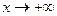 . Довести, що знайдеться число
. Довести, що знайдеться число 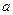 , для якого рівняння
, для якого рівняння 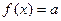 має нескінченно багато розв'язків.
має нескінченно багато розв'язків.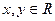 рівності
рівності  .
. на
на 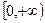 .
.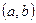 функцій - рівномірно неперервна.
функцій - рівномірно неперервна.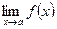 та
та 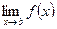 Довести, що
Довести, що 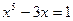 має хоча б один корінь на (1;2).
має хоча б один корінь на (1;2).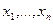 - будь-які значення з
- будь-які значення з  , таке, що
, таке, що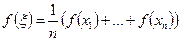
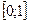 та множина її значень належить
та множина її значень належить 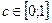 таке, що
таке, що 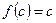 .
.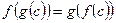 .
.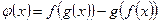 .
. ))
)) 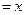 для будь-якого
для будь-якого 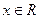 . Довести, що існує точка с, в якій
. Довести, що існує точка с, в якій 
 .
. , послідовність
, послідовність  збігається до одного з розв'язків рівняння
збігається до одного з розв'язків рівняння 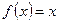 .
.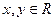 рівності
рівності 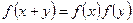 .
.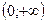 функції, задовольняючі для будь-яких
функції, задовольняючі для будь-яких  рівності
рівності 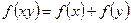 .
.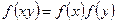 .
.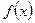 на проміжку X задовольняє умові Ліпшица:
на проміжку X задовольняє умові Ліпшица: , то вона неперервна на X.
, то вона неперервна на X.
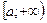 , то
, то 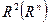 зв’язна тоді і тільки тоді, коли будь-які дві точки з цієї множини можна з’єднати неперервною кривою, що цілком належить множині.
зв’язна тоді і тільки тоді, коли будь-які дві точки з цієї множини можна з’єднати неперервною кривою, що цілком належить множині.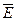 - зв’язна.
- зв’язна.


