
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
І. Обробка даних безпосереднього вимірюванняСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте а) Обробка даних вимірювання довжини 1.Визначення середнього арифметичного значення довжини І:
2.Визначення похибок окремих вимірювань довжини
3.Визначення середньої похибки вимірювання довжини 4.Визначення відносної похибки вимірювання як виразу точності:
(заокруглення скрізь з перебільшенням). 5.Результат вимірювання довжини маятника:
б) Обробка даних вимірювання періоду T коливання маятника. .Визначення середнього арифметичного значення періоду коливання Т:
2. Визначення похибок окремих вимірювань періоду: ∆T1 = 3,12 — 3,10= + 0,02 с, ∆Т2 = 3,12 — 3,14 = - 0,02 с, ∆T3 = 3,12 — 3,11 = + 0,01 с, ∆Т4 = 3,12 — 3,15 = - 0,03 с, ∆T5 = 3,12 — 3,10 = + 0,02 с. 3.Визначення середньої похибки вимірювання періоду коливання:
4.Визначення відносної похибки вимірювання періоду: 5.Результат вимірювання періоду коливання маятника:
II. Підрахунок результату експерименту 1.Установлення розрахункової формули. З формули періоду коливань математичного маятника випливає
2.Підрахунок величини прискорення g. Підставивши числові значення l і Т, дістаємо
3.Виведення формули для підрахунку похибки знайденого значення £. Оскільки розрахункова формула є часткою, то підрахунок похибки розпочнемо з відповідної похибки. На основі рядків 4 і 5 табл. на с. 10 маємо:
4.Обчислення відносної похибки знайденого результату:
5.Обчислення похибки результату експерименту:
6.Установлення числової величини результату експерименту. Якщо десяті в запису числа 9,89 сумнівні, то соті — тим більше. Заокругливши його до десятих, дістаємо:
III.Висновки Результат експерименту показує, що числове значення прискорення вільного падіння на місці досліду повинно задовольняти нерівність: 9,7 <g<10,l м/с2. Так експериментально встановлюють верхню і нижню границі прискорення вільного падіння g. Правильність такого висновку підтверджується тим, що вірне значення g (взяте з довідника для певної місцевості) дійсно вкладається в ці границі. Примітка. Наведена схема обробки результатів вимірювань з однією запасною цифрою (l) корисна для початківців, проте не завжди виправдана. У багатьох випадках результат можна дістати швидше, якщо перед початком роботи проаналізувати розрахункову формулу для сумарної похибки з точки зору похибок, які дають наявні прилади і методи вимірювання. Так, у розглянутому прикладі з формули похибок (2) випливає, що при визначенні g велику похибку дає вимірювання Т (похибка Т подвоюється). В учбових лабораторіях при знаходженні g маятником звичайний секундомір дає можливість визначити період коливання з точністю до трьох значущих цифр. Тому четверту значущу цифру як запасну при вимірюваннях і розрахунках З результатів вимірювань
При визначенні На закінчення наведемо зразок оформлення звіту про виконану роботу. Його теоретичну частину з малюнками, схемами і розграфленою таблицею для заповнення результатами досліду підготовляють дома. На лабораторному занятті виконують вимірювання, обчислюють результати, їх похибки. Зразок ЛАБОРАТОРНА РОБОТА № 4 Визначення прискорення вільного падіння за допомогою маятника. Математичним маятником називають коливну систему що складається з матеріальної точки, підвішеної на тонкій і нерозтяжній нитці. Період коливань Т маятника, його довжина
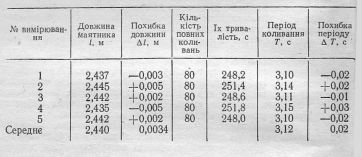
яку можна застосовувати лише при малих кутах відхилення (2—4°). Довжину маятника виміряно лінійкою, період коливання вираховано як частку від ділення часу декількох десятків коливань (вимірювали секундоміром) на їх число. Результати вимірювання наведено в таблиці:
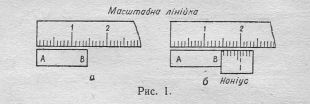
§ 4. ОСНОВНІ ПРИЛАДИ ДЛЯ ПІДВИЩЕННЯ ТОЧНОСТІ ВИМІРЮВАНЬ Ноніус. Операція безпосереднього вимірювання зводиться до порівняння вимірюваної величини з масштабом. Так, вимірюючи довжину тіла АВ (рис. 1, а), прикладають його до масштабної лінійки і порівнюють безпосередньо, у скільки разів довжина тіла більша за довжину найменшої поділки масштабу (відлічують поділки проти кінців А і .В). При цьому кількість десятих частин поділки оцінюють на око. Якщо довжину поділки взято за одиницю, то таке порівняння дасть кількість одиниць довжини і їх часток у тілі. Точність відліку по шкалі обмежується ціною її поділки, тобто значенням найменшої поділки. Око може впевнено відрізняти, в якій з половин поділки міститься край вимірюваного предмета. Тому вважають, що точність вимірювання становить не більше половини ціни найменшої поділки шкали. Точність до десятої частини поділки може дати лише добре треноване око, але й воно краще впорається з цим за допомогою ноніуса або мікрометричного гвинта. Ноніусом називають допоміжну лінійку, яку застосовують разом з масштабною для відлічування десятих, двадцятих або п’ятдесятих-часток міліметра. Якщо ноніус призначено для вимірювання десятих часток міліметра, то на ньому відстань 19 або 9 мм поділено на 10 рівних частин. Тут довжина кожної поділки ноніуса становить 1,9 або 0,9 мм, отже, розбіжність між однією поділкою лінійки і однією поділкою ноніуса становить 0,1 мм. Це число називають точністю ноніуса. Якщо приставити таку ноніусну лінійку до тіла, довжина якого більша за 14 мм і менша за 15 мм (рис. 1, б), то коли шоста поділка ноніуса збігається з будь-якою поділкою масштабної лінійки, різниця між кінцем В тіла і чотирнадцятою поділкою масштабної лінійки становитиме 0,6 мм, тобто загальна довжина тіла буде 14,6 мм. Оскільки точність вимірювання визначається точністю ноніуса, то в цьому випадку вона буде 0,1 мм. У загальному випадку, якби в ноніусі п — 1 поділок масштабної лінійки були поділені на п частин, то при довжині тіла АВ, що становить т цілих поділок масштабу і при збігу ℜ-ї поділки ноніуса з будь-якою поділкою масштабної лінійки довжина тіла дорівнювала б AB = Практичне застосування ноніус має в штангенциркулі для вимірювання довжини, у коловому ноніусі — для вимірювання градусів дуги тощо. Мікрометричний гвинт. Мікрометричний гвинт є основною частиною ряду приладів, наприклад мікрометра, приладу для вимірювання товщини з точністю до 0,01; 0,02; 0,04 мм. Мікрометр (рис. 2) складається з масивної скоби А з полірованою п’яткою В на одному кінці, а через другий кінець М проходить мікрометричний гвинт СБ з кроком різі 0,5 мм. До останнього прикріплено барабан Б, який по ободу НК поділений на 50 поділок. На поверхні гвинтової муфти М зроблено міліметрові поділки так, що коли край барабана (НК) збігається з 0 шкали //, кінець С мікрометричного гвинта доторкається до п’ятки.
Якщо хід гвинта становить 0,5 мм, а обід барабана має 50 поділок, то при повертанні барабана на одну поділку відстань ВС змінюється на 0,01 мм, при повертанні на дві поділки — на 0,02 мм і т. д. Отже, відстань ВС завжди дорівнює такому числу міліметрових і пів міліметрових поділок, скільки поділок масштабної лінійки // повністю вийшло з-під барабана, плюс стільки сотих частин міліметра, скільки показує номер поділки барабана, яка збігається з лінією //. Щоб мікрометричний гвинт завжди точно однаково тиснув на вимірюване тіло, яке міститься між точками В і С, до барабана Б прикріплено спеціальну запобіжну головку або тріскачку Т. Підводячи мікрометричний гвинт близько до п’ятки або вимірюваного тіла, обертати барабан пальцями перестають і продовжують його обертати за допомогою тріскачки. __________________________________________________________ РозділІІ ЛАБОРАТОРНІ РОБОТИ Робота І ПЕРЕВІРКА ЗАКОНІВ ПРЯМОЛІНІЙНОГО РУХУ НА ПРИЛАДІ АТВУДА Устаткування: прилад Атвуда з набором важків, секундомір. Теоретичний вступ
Якщо на систему діяти сталою силою і безперервно, наприклад вагою додаткового важка Ра, то система важків, набуваючи сталого прискорення, рухатиметься рівно прискорено. Величина цього прискорення а визначається другим законом динаміки: прискорення, якого набуває тіло під дією сили F дорівнює відношенню цієї сили до маси тіла m, тобто а = У цьому випадку діюча сила дорівнює вазі додаткового важка Ра = mag, маса рухомої системи дорівнює сумі мас обох важків 2m і додаткового важка ma. Тому
При такому рівноприскореному русі без початкової швидкості шлях з повинен змінюватись пропорційно квадрату часу руху t S= а швидкість v — пропорційно його першому степеню v=at (3) Звідси випливає, що шлях s1 за першу секунду руху чисельно дорівнює половині прискорення s1= a=v1=2s1 (4) Це дає нам основу дослідної перевірки прискорення а, знайденого за законами динаміки: прискорення а чисельно повинно бути вдвічі більшим за шлях пройдений за першу секунду, і повинно чисельно дорівнювати швидкості v1, набутій в кінці першої секунди. Величину s1 можна виміряти на досліді безпосередньо. Що ж до швидкості v1 в кінці першої секунди, то слід пригадати, що вона дорівнює тій швидкості рівномірного руху, яку мало б тіло, якби, починаючи з кінця першої секунди, воно рухалося рівномірно. Швидкість рівномірного руху чисельно дорівнює шляху, пройденому за секунду. Виходячи з викладеного, перевірити закони динаміки і кінематики можна так. 1)Протягом першої секунди систему примушують рухатись рівно прискорено під дією сталої сили ваги важка Ра. 2) Довжину шляху s1, пройденого за цей час, вимірюють безпосередньо, спостерігаючи з секундоміром за рухом важків уздовж шкали. 3)В кінці першої секунди затримують прискорюючий важок Ра, надаючи системі можливість рухатись без прискорення з швидкістю, набутою системою до цього часу. 4)Продовжуючи спостерігати за рухом важків уздовж шкали, вимірюють відстань, пройдену за другу секунду при рівномірному русі. Вона чисельно дорівнює швидкості v 1. 5)Порівнюють прискорення, знайдені за результатами п. 2 і п. 4 на основі (4), з прискоренням, обчисленим за законами динаміки (1).
|
||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 824; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |

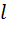 маятника.
маятника.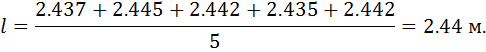
 .
.


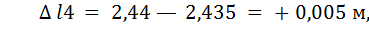

 :
: 
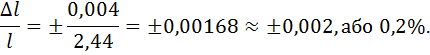
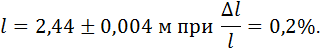
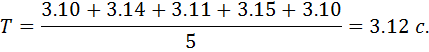
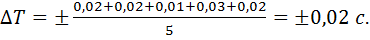

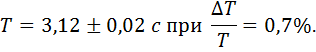
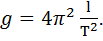 (1)
(1)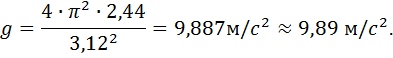
 (2)
(2)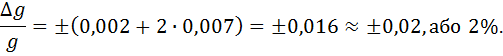

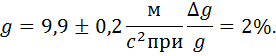
 брати недоцільно.
брати недоцільно.
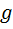 з таким заокругленим значенням
з таким заокругленим значенням 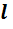 і прискорення вільного падіння g зв'язані формулою.
і прискорення вільного падіння g зв'язані формулою.

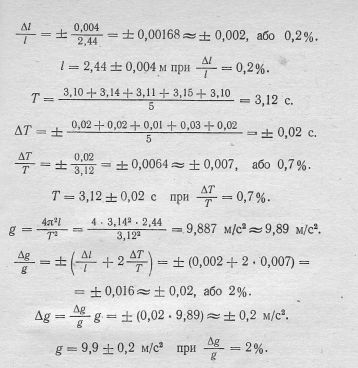
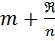 мм і з точністю до
мм і з точністю до  мм.
мм.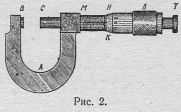 При цьому нульова поділка барабана буде проти масштабної лінійки //.
При цьому нульова поділка барабана буде проти масштабної лінійки //. Прилад Атвуда складається з високого вертикального стояка (рис. 3), який має на верхньому кінці блок Б, що має обертатися з малим тертям. Якщо до кінців гнучкої нитки, перекинутої через блок, підвісити важки Р1 і Р2 однакової маси т, то в полі земного тяжіння вся система важків з ниткою буде в рівновазі. Від короткого імпульсу руки система набуде певної швидкості і, рухаючись за інерцією, зберігатиме її сталою згідно з першим законом динаміки (в міру можливості нехтувати тертям).
Прилад Атвуда складається з високого вертикального стояка (рис. 3), який має на верхньому кінці блок Б, що має обертатися з малим тертям. Якщо до кінців гнучкої нитки, перекинутої через блок, підвісити важки Р1 і Р2 однакової маси т, то в полі земного тяжіння вся система важків з ниткою буде в рівновазі. Від короткого імпульсу руки система набуде певної швидкості і, рухаючись за інерцією, зберігатиме її сталою згідно з першим законом динаміки (в міру можливості нехтувати тертям). .
. (1)
(1)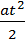 (2)
(2) ,а швидкість у кінці першої секунди v1 чисельно дорівнює прискоренню (v = а). Об’єднуючи ці два висновки, дістанемо чисельну рівність:
,а швидкість у кінці першої секунди v1 чисельно дорівнює прискоренню (v = а). Об’єднуючи ці два висновки, дістанемо чисельну рівність:


