
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вимірювання. Класифікація вимірюваньСодержание книги
Поиск на нашем сайте
Зміст
Теоретична частина Вимірювання. Класифікація вимірювань Найбільш поширеними характеристиками матеріальних об’єктів та процесів є величини і залежності між ними. Якраз про них створюється інформація за допомогою засобів вимірювання. Вимірювання є дуже різноманітними і кількість їх різновидів зростає. Свідченням цього є динамічні вимірювання та сумісні вимірювання величини. Для класифікації вимірювань необхідно встановити їх найбільш суттєві ознаки. До найбільш суттєвих ознак різних вимірювань відносять: - відсутність чи наявність в процедурі вимірювання перетворення роду вимірюваної величини та обчислення її значення за відомими залежностями; - вид рівняння вимірювання; - призначення вимірювання для незмінних чи змінних в часі вимірюваних величин; - особливості визначення похибок вимірювання; - наявність чи відсутність розмірності у вимірюваної величини; - співвідношення між кількістю вимірюваних величин та кількістю вимірювань. За відсутністю чи наявністю в процедурі перетворення роду фізичної величини та обчислення її значення за відомими залежностями вимірювання класифікують на прямі та непрямі. Пряме вимірювання – це вимірювання однієї фізичної величини, значення якої знаходять безпосередньо без перетворення її роду та використання відомих залежностей. Для реалізації прямих вимірювань фізичної величини Х необхідно мати компаратор а також багатозначну міру з відповідним діапазоном зміни значень, чи однозначну міру та масштабний вимірювальний перетворювач. При всіх інших однакових умовах прямим вимірюванням властиві мінімальні похибки.
Непряме вимірювання – це вимірювання, у якому значення однієї чи декількох вимірювальних величин знаходять після перетворення роду величини та обчислення за відомим залежностями їх від декількох величин аргументів, що вимірюються прямо. Непрямі вимірювання поділяються на опосередковані, сумісні та сукупні. Опосередковане вимірювання – це непряме вимірювання однієї величини з перетворенням її роду чи обчисленням за результатами вимірювання інших фізичних величин, з якими вимірювана величини пов’язана явною функційною залежністю. Сукупне вимірювання – це непряме вимірювання, в якому значення декількох одночасно вимірюваних однорідних величин отримують розв’язанням рівнянь, що пов’язують різні сполучення цих величин, які вимірюються прямо чи опосередковано. Сумісне вимірювання – непряме вимірювання, в якому значення декількох одночасно вимірюваних різнорідних фізичних величин отримують розв’язанням рівнянь, які пов’язують їх з іншими фізичними величинами, що вимірюються прямо чи опосередковано. Сумісні вимірювання є різновидом вимірювання залежностей. За призначенням вимірювань для незмінних чи змінних у часі вимірювальних величин їх класифікують на статичні та динамічні вимірювання. Статичне вимірювання – вимірювання величини, яку можна вважати незмінною за час вимірювання (коли похибкою, що виникає від її зміни, можна знехтувати). Динамічне вимірювання – це вимірювання величини, що змінюється за час вимірювання. Вимірювання за ознакою особливостей визначення їх похибок класифікують на лабораторні та технічні. Лабораторні вимірювання – це вимірювання за яких похибки кожного результату вимірювання оцінюють за даними, що одержані при цьому вимірюванні. Технічні вимірювання – це вимірювання, які виконуються в заданих умовах згідно з зробленою та рекомендованою раніше методикою, при цьому похибки вимірювання, які при її виконанні окремо не визначають, повинні бути нижче встановлених нею. Вимірювання фізичної величини за наявністю або відсутністю розмірності у вимірюваних величин поділяють на вимірювання розмірних величин(абсолютні) та вимірювання безрозмірних величин(відносні). Відносне вимірювання – це вимірювання відношення величини до іншої однорідної величини.
Вимірювання фізичної величини за співвідношенням між кількістю виміряних величин ті кількістю вимірювань поділяють на не надлишкові одноразові та надлишкові, які виконуються або одно канально багаторазово, або багатоканально одноразово, зокрема, із метою зниження рівня випадкових похибок шляхом усереднення.
Похибки виміювання Похибки засобів вимірювання Різні види засобів вимірювання виконують різні функції, причому кожному з них приписують деякі номінальні характеристики. Дійсні характеристики засобів вимірювання не співпадають з номінальними, що і визначає їх похибки. Похибки засобів вимірювання представляють у вигляді абсолютних, відносних чи зведених похибок. Абсолютною похибкою засобу вимірювання називають різницю між показом засобу вимірювань та істинним значенням вимірюваної величини за відсутності методичних похибок і похибок від взаємодії засобу вимірювання за об’єктом вимірювання. Δзв = Хзв – Хі. Відносною похибкою засобу вимірювання називають відношення абсолютної похибки засобів вимірювань до істинного значення вимірюваної величини. δзв[%] = (Δ зв/Хі) 100%. Щоб було можливим порівнювати за точністю різні прилади з різними границями вимірювань, введено поняття зведеної похибки вимірювального приладу. Зведена похибка засобу вимірювань називають відношення абсолютної похибки засобу вимірювань до нормованого значення. γ[%] = (Δ зв/Хн) 100%, де Хн – нормоване значення. Похибки засобів вимірювання містять ряд систематичних і випадкових складових, статичні та динамічні похибки, які визначаються аналогічно визначенням похибок вимірювань. Щоб наперед оцінити похибку, яку внесе дане устаткування в кінцевий результат, користуються нормованими значеннями похибки. Під нормованим значенням розуміють похибки, які є граничними для даного типу засобів вимірювання. Стандартами регламентуються способи нормування і форми вираження допустимих границь похибок. Границею допустимої похибки засобу вимірювань називають найбільше значення без урахування знаку похибки засобу вимірювання, за яким цей засіб ще може бути визнаний придатним до застосування. Адитивна похибка – складова абсолютної похибки засобу вимірювальної техніки, яка не залежить від вимірювальної величини. Мультиплікативна – складова похибки засобу вимірювання, яка пропорційна вимірювальній величині. Для нормування похибок засобів вимірювальної техніки з адитивною і мультиплікативною похибками найбільш поширеною формою запису є: δн = ±[c + d·(|Хн/Х| - 1)], де Хн – нормоване значення, с,d – постійні числа. Суть с полягає у тому, що це є границя допустимої відносної похибки при максимальному показі приладу, d – межа допустимої похибки при нульовому показанні приладу, яка виражена у відсотках до верхньої межі вимірювання, [(Хн/Х) – 1] – зростання відносної похибки при зменшенні показань приладу. Узагальненою характеристикою засобу вимірювальної техніки є клас точності, що виражається границями його допустимих основної і додаткових похибок а також іншими характеристиками, що впливають на його точність, значення яких регламентується. Клас точності характеризує точність засобу вимірювання, але не є безпосередньою характеристикою точності вимірювання, виконаного за допомогою даного засобу вимірювання.
В основу присвоєння класу точності береться основна похибка засобу вимірювання і спосіб її вираження. Якщо основна похибка виражається в одиницях вимірюваної величини або в поділках шкали, то класи точності позначають порядковими номерами. Номери визначаються відповідними стандартами. Для засобів вимірювання, відлікові пристрої яких градуюються у логарифмічних одиницях, позначення класів точності зберігається з граничними значеннями допустимих похибок. Якщо границі допустимої основної похибки задаються відносною або зведеною похибкою, то позначення класів точності вибирають із наведеного раніше ряду. Якщо границі допустимої основної похибки залежать від значення вимірюваної величини, наприклад 0,02/0,01.
Прямі вимірювання Прямі багатократні вимірювання поділяються на рівно- та нерівноточні. Рівноточними називаються вимірювання, що проводяться засобами вимірювань однакової точності за однією і тією ж методикою при незмінних зовнішніх умовах. При рівноточних вимірюваннях СКВ результатів всіх рядів вимірювань рівні між собою. Перед проведенням обробки результатів вимірювань необхідно переконатись в тому, що дані із вибірки, що оброблюється, статистично підконтрольні, групуються навколо одного й того ж центра і мають однакову дисперсію. Стійкість змін часто оцінюють інтуїтивно на основі тривалих спостережень. Однак існують математичні методи розв’язку поставленої задачі – так звані методи перевірки однорідності. Щодо вимірювань, то розглядається однорідність груп спостережень, необхідні ознаки якої полягають в оцінці незміщеності середніх арифметичних і дисперсій відносно один одного. Перевірка допустимості різниці між оцінками дисперсій нормально розподілених результатів вимірювань виконується за допомогою критерія Р.Фішера за наявністю двох груп спостережень і критерія М.Бартлетта, якщо груп більше. Задача обробки результатів багатократних вимірювань полягає в знаходженні оцінки вимірюваної величини та довірчого інтервала, в якому знаходиться її дійсне значення. Обробка має проводитись у відповідності до ГОСТ8.207-76 “ГСИ. Прямі вимірювання з багатократними спостереженнями. Методи обробки результатів спостережень. Загальні положення”. Вихідною інформацією для обробки э ряд із n (n>4) результатів вимірювань х1, х2, х3,…, хn, з яких виключені відомі систематичні похибки, – вибірка. Число n залежить як від вимог до точності результату, так і від реальної можливості виконувати повторні зміни.
Послідовність обробки результатів прямих багатократних вимірювань складається з ряду етапів. - визначення точкових оцінок закону розподілу результатів вимірювань. На даному етапі визначаються: середнє арифметичне значення У ряді випадків для більш надійної ідентифікації закону розподілу результатів вимірювань можуть визначатись інші точкові оцінки: - коефіцієнт асиметрії, ексцес і контрексцес, ентропійний коефіцієнт; - визначення закону розподілу результатів вимірювань або випадкових похибок вимірювань. - оцінка закона розподілу за статистичними критеріями. При кількості спостережень n>50 для ідентифікації закону розподілу використовується критерій Пірсона або критерій Мізеса-Смірнова. При 50>n>15 для перевірки нормальності закону розподілу застосовується составний критерій, наведений в ГОСТ 8.207-76. При n<15 приналежність експерментального розподілу до нормального не перевіряється; - визначення довірчих меж випадкової похибки. Якщо вдалося ідентифікувати закон розподілу результатів вимірювань, то з його використанням знаходять квантильний множник zp при заданому значенні довірчої ймовірності Р. В цьому випадку довірчі межі випадкової похибки - визначення меж невиключеної систематичної похибки θ результату вимірювань. Межі невиключеної систематичної похибки приймають рівними межам допустимих основних і додаткових похибок засобів вимірювання, якщо їх випадкові складові дуже малі. Довірча ймовірність при визначенні меж θ приймається рівною довірчій ймовірності, що використовується при знаходженні меж випадкової похибки; - визначення довірчих меж похибки результату вимірювання Δр. Така операція здійснюється шляхом додавання СКВ випадкової складової - запис результату вимірювання. Результат вимірювання записується у вигляді
Практична частина Завдання 1 Проведено вимірювання за допомогою вольтметра з Оцінити граничні значення основної та додаткових похибок. Оцінити граничну та дорічні похибки вимірювання (
Розв’язання Похибка вимірювання складається з основної інструментальної, яка визначається за класом точності вольтметра та додаткових, зумовлених відхиленням температури навколишнього середовища від нормальної, наявність зовнішнього магнітного поля та відхилення напруги живлення поза межі допустимих значень.
1. Оскільки клас точності приладу нормовано сталими с та d, а саме 0.1/0.01, то основна відносна гранична похибка вимірювання напруги
2. Нормальний діапазон температури навколишнього середовища від 18 до 22
3. Напруженість зовнішнього магнітного поля Н=400 А/м, тому додаткова відносна гранична похибка зумовлена ци фактором
4. Діапазон гранично допустимих значень напруги живлення
Оскільки напруга живлення приладу становить 205 В, що є менше менше від нижньої межі, але входить в діапазон 187-240В, то зумовлена цим відносна гранична похибка
5. Тобто сумарна відносна гранична похибка вимірювання напруги
Запишемо результат вимірювання напруги враховуючи, що похибку досить заокруглити до однієї або двох значущих цифр і кількість знаків після коми в написанні результату повинна відповідати кількості цих знаків у похибці. Тобто
Завдання 2. Вивести вирази абсолютної та відносної похибок опосередкованого вимірювання величини Записати вирази похибок при Розв’язання: Абсолютну похибку опосередкованого вимірювання можна визначити через повний диференціал виразу цього вимірювання. А саме
Тут
Відносна похибка (у відносних одиницях)
При
Завдання 3. Для отримання 12 результатів спостережень при прямих рівно точних вимірюваннях: 7.13 6.94 7.15 7.31 7.26 7.53 6.68 6.59 6.76 7.9 7 6.54 визначити оцінку результату вимірювань; оцінку дисперсії та с. к. в. випадкових похибок окремих результатів; оцінку с. к. в. результату вимірювання. Оцінити довірчі границі похибки для
Розв’язання: Найкращою оцінкою багатократних прямих рівно точних вимірювань, що дає змогу зменшити вплив випадкових складових похибки вимірювання кожного окремого спостереження, є середнє значення
Незміщена оцінка дисперсії сукупності спостережених значень
6,54; 6,59; 6,68; 6,76; 6,94; 7,00; 7,13; 7,15; 7,26; 7,31; 7,53; 7,90. Перевіримо крайні члени ряду на аномальність. Знайдемо співвідношення
За табл.1 (додаток), що задає допустимі значення про нормованих відхилень від середнього і заданою довірчою ймовірністю, знайдемо
Оскільки кількість спостережень
Завдання 4 Для оцінювання результату опосередкованого вимірювання величини
Розв’язання: Похибку опосередкованого вимірювання шукаємо за похибками прямих вимірювань. Зокрема, відносна похибка
Результати рівно точних взаємнонезалежних спостережень величин Х та У містять випадкові похибки. Тому найкращою оцінкою кожної з безпосередньо вимірюваних величин (Х та У) та опосередкованої величини U будуть їх середні значення, тобто
За визначенням абсолютна похибка Тому дисперсія абсолютної похибки усередненого результату посереднього вимірювання
Так само пов’язані і їх незміщені оцінки
Своєю чергою дисперсія похибок кожної з усереднених величин
Незміщені оцінки дисперсії спостережень
А дисперсій відповідних середніх значень Звідси
Для
Завдання 5 Для результатів вимірювань величин Х= -4; -3; -2; -1; 0; 1 та У=2; 2.97; 3.99; 4.99; 6.02; 7.05 за допомогою методу найменших квадратів (МНК) визначити коефіцієнти лінійної залежності між ними. Розв'язання: За умовою вважається, що залежність між величинами Y та Х є лінійною, тобто Y=kX+b. Необхідно знайти два невідомі параметри k й Ь, опрацьовуючи набори результатів спостережень {х,} та {у,} за методом найменших квадратів. Сформуємо відповідні рівняння, а саме: знайдемо часткові похідні функції Y за невідомими параметрами
Одержимо систему двох рівнянь з двома невідомими, а саме:
Звідси
Знайдемо k=1,b=6. Отже Y=X+6.
Завдання 6 Сформуйте систему нормальних рівнянь за методом найменших квадратів для результатів сукупних вимірювань. Оцінити СКВ. Знайти нев’язки. Записати результат вимірювання. Результати сукупних вимірювань див. табл. 6
Розв’язання Складемо систему нормальних рівнянь:
де коефіцієнти
Врахувавши значення даних коефіцієнтів система нормальних рівнянь матиме вигляд:
Головний визначник цієї системи D = 156. Найбільш ймовірні значення невідомих дорівнюють:
Підставляємо значення найбільш ймовірних значень до умовних рівнянь: x1 + x2 + x3 + x4 = 1.065 + 7.045 + 1.052 + 5.081 = 14.243, x2 + x3 = 7.045 + 1.052 = 8.097, x1 + x2 = 1.065 + 7.045 = 8.11, x3 + x4 = 1.052 + 5.081 = 6.133, x1 + x2 + x3 + x4 = 1.065 + 7.045 + 1.052 = 9.162, x1 + x2 + x3 = 1.065 + 1.052 + 5.081 = 7.098, x1 + x3 + x4 = 1.065 +1.052 + 5.081 = 7.198, x1 + x3 + x4 = 1.065 + 5.081 + 1.052 = 7.198, x2 + x4 = 7.045 + 5.081 = 12.126, x1 + x3 = 1.052 + 1.065 = 2.117. Знаходимо нев´язки
Знайдемо границі довірчого інтервалу
і аналогічно для інших невідомих. Для цього розрахуємо значення ад’юнктів. S11=70, S22=72, S33 = 72, S44 = 52
Для m-n=5 та ймовірності Р=0,95 коефіцієнт Ст´юдента дорівнює tp = 2.571 Розрахуємо границі довірчого інтервалу
Отже, результат вимірювання
Розрахунки реалізовані за допомогою математичного пакету Mathcad і наведені у додатку. Література Орнатский П.П. Теоретические основы информационно-измерительной техники. – К.: Вища школа, 1983 - 455 с. 1. Володарський Є.Т., Кухарчук В.В., Поджаренко В.О., СердюкГ.Б. Метрологічне забезпечення вимірювань і контролю. Навчальний посібник. – Вінниця: Велес,2001. – 219 с. 2. Сена Л.А. Единицы физических величин и их размерности: Учебно-справочное руководство, - 3-е изд., перераб. и доп. – М.: Наука. Гл. ред. физ.-мат. лит., 1988. – 432 с. 3. Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений. – Л.: Энергоатомидат, 1985 – 321 с. 4. Шишкин И.Ф. Теоретическая метрология. – М.: Изд-во стандартов, 1991 – 287 с. 5. Грановский В.А. Динамические измерения. – Л.: Энергоатомидат, 1984 – 353 с. 6. Селиванов М.Н., Фридман А.Э., Кудряшова Ж.Ф. Качество измерений: Метрологическая справочная книга. – Л.:Лениздат, 1987. – 295 с. 7. Федоров А.М., Цыган Н.Я., Мичурин В.И. Метрологическое обеспечение электронных средств измерений электрических величин: Справочная книга – Л.: Энергоатомидат, Ленингр. отд-ние. 1988. – 208 с. Зміст
Теоретична частина Вимірювання. Класифікація вимірювань Найбільш поширеними характеристиками матеріальних об’єктів та процесів є величини і залежності між ними. Якраз про них створюється інформація за допомогою засобів вимірювання. Вимірювання є дуже різноманітними і кількість їх різновидів зростає. Свідченням цього є динамічні вимірювання та сумісні вимірювання величини. Для класифікації вимірювань необхідно встановити їх найбільш суттєві ознаки. До найбільш суттєвих ознак різних вимірювань відносять: - відсутність чи наявність в процедурі вимірювання перетворення роду вимірюваної величини та обчислення її значення за відомими залежностями; - вид рівняння вимірювання; - призначення вимірювання для незмінних чи змінних в часі вимірюваних величин; - особливості визначення похибок вимірювання; - наявність чи відсутність розмірності у вимірюваної величини; - співвідношення між кількістю вимірюваних величин та кількістю вимірювань. За відсутністю чи наявністю в процедурі перетворення роду фізичної величини та обчислення її значення за відомими залежностями вимірювання класифікують на прямі та непрямі. Пряме вимірювання – це вимірювання однієї фізичної величини, значення якої знаходять безпосередньо без перетворення її роду та використання відомих залежностей. Для реалізації прямих вимірювань фізичної величини Х необхідно мати компаратор а також багатозначну міру з відповідним діапазоном зміни значень, чи однозначну міру та масштабний вимірювальний перетворювач. При всіх інших однакових умовах прямим вимірюванням властиві мінімальні похибки. Непряме вимірювання – це вимірювання, у якому значення однієї чи декількох вимірювальних величин знаходять після перетворення роду величини та обчислення за відомим залежностями їх від декількох величин аргументів, що вимірюються прямо. Непрямі вимірювання поділяються на опосередковані, сумісні та сукупні. Опосередковане вимірювання – це непряме вимірювання однієї величини з перетворенням її роду чи обчисленням за результатами вимірювання інших фізичних величин, з якими вимірювана величини пов’язана явною функційною залежністю. Сукупне вимірювання – це непряме вимірювання, в якому значення декількох одночасно вимірюваних однорідних величин отримують розв’язанням рівнянь, що пов’язують різні сполучення цих величин, які вимірюються прямо чи опосередковано. Сумісне вимірювання – непряме вимірювання, в якому значення декількох одночасно вимірюваних різнорідних фізичних величин отримують розв’язанням рівнянь, які пов’язують їх з іншими фізичними величинами, що вимірюються прямо чи опосередковано. Сумісні вимірювання є різновидом вимірювання залежностей. За призначенням вимірювань для незмінних чи змінних у часі вимірювальних величин їх класифікують на статичні та динамічні вимірювання. Статичне вимірювання – вимірювання величини, яку можна вважати незмінною за час вимірювання (коли похибкою, що виникає від її зміни, можна знехтувати). Динамічне вимірювання – це вимірювання величини, що змінюється за час вимірювання. Вимірювання за ознакою особливостей визначення їх похибок класифікують на лабораторні та технічні. Лабораторні вимірювання – це вимірювання за яких похибки кожного результату вимірювання оцінюють за даними, що одержані при цьому вимірюванні. Технічні вимірювання – це вимірювання, які виконуються в заданих умовах згідно з зробленою та рекомендованою раніше методикою, при цьому похибки вимірювання, які при її виконанні окремо не визначають, повинні бути нижче встановлених нею. Вимірювання фізичної величини за наявністю або відсутністю розмірності у вимірюваних величин поділяють на вимірювання розмірних величин(абсолютні) та вимірювання безрозмірних величин(відносні). Відносне вимірювання – це вимірювання відношення величини до іншої однорідної величини. Вимірювання фізичної величини за співвідношенням між кількістю виміряних величин ті кількістю вимірювань поділяють на не надлишкові одноразові та надлишкові, які виконуються або одно канально багаторазово, або багатоканально одноразово, зокрема, із метою зниження рівня випадкових похибок шляхом усереднення.
Похибки виміювання
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 301; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.38.54 (0.011 с.) |

 вимірюваної величини; СКВ результату вимірювання
вимірюваної величини; СКВ результату вимірювання  ; СКВ середнього арифметичного значення
; СКВ середнього арифметичного значення 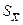 .
. ;
; при довірчій імовірності P=Pд.
при довірчій імовірності P=Pд. В, кл. т. 0.1/0.01 отримано показ
В, кл. т. 0.1/0.01 отримано показ  В. Вимірювання здійснено при температурі навколишнього середовища
В. Вимірювання здійснено при температурі навколишнього середовища  , магнітному полі напруженістю Н=400 А/м, напруга живлення приладу 205В. Температурна похибка не перевищує основну на кожних
, магнітному полі напруженістю Н=400 А/м, напруга живлення приладу 205В. Температурна похибка не перевищує основну на кожних  відхилення температури від нормальної області (20
відхилення температури від нормальної області (20  2)
2)  , магнітна – половини від основної при напруженості зовнішнього поля до 400 А/м, при відхиленні напруги живлення за межі 220 В
, магнітна – половини від основної при напруженості зовнішнього поля до 400 А/м, при відхиленні напруги живлення за межі 220 В  ). Записати результати вимірювання.
). Записати результати вимірювання.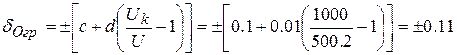
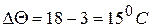 . Тому зумовлена цим відносна гранична похибка.
. Тому зумовлена цим відносна гранична похибка.
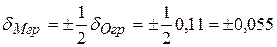

 .
. 6. Абсолютна гранична похибка вимірювання напруги
6. Абсолютна гранична похибка вимірювання напруги
 .
. .
. .
. .
. ;
;  ;
;  .
. .
. .
. знайдемо
знайдемо

 . Записати результат.
. Записати результат.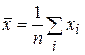 .
. Проаналізуємо чи немає серед спостережень грубих (аномальних) помилок. Сформуємо із спостережень варіаційний ряд (від найменшого значення до найбільшого)
Проаналізуємо чи немає серед спостережень грубих (аномальних) помилок. Сформуємо із спостережень варіаційний ряд (від найменшого значення до найбільшого)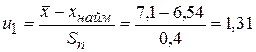

 , а саме: для
, а саме: для  , а отже, надійності
, а отже, надійності  , та n=12 маємо
, та n=12 маємо  . Оскільки
. Оскільки  та
та  менші від
менші від  , то кратні значення (варіанти) варіаційного ряду не треба розглядати, як аномальні. Незміщена оцінка середньоквадратичного відхилення середнього значення
, то кратні значення (варіанти) варіаційного ряду не треба розглядати, як аномальні. Незміщена оцінка середньоквадратичного відхилення середнього значення
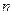 < 30, то при оцінюванні гарантійного (довірчого) інтервалу для похибки середнього доцільно скористатися не розподілом Гауса, а Стьюдента. За табл.. 2 (додаток), що задає допустимі значення гарантійного коефіцієнта для заданої гарантійної (довірчої) ймовірності, знайдемо відповідний коефіцієнт. А саме для n=12,
< 30, то при оцінюванні гарантійного (довірчого) інтервалу для похибки середнього доцільно скористатися не розподілом Гауса, а Стьюдента. За табл.. 2 (додаток), що задає допустимі значення гарантійного коефіцієнта для заданої гарантійної (довірчої) ймовірності, знайдемо відповідний коефіцієнт. А саме для n=12,  =0,95,
=0,95,  =2,201. Отже, результат вимірювання
=2,201. Отже, результат вимірювання
 виконані по 9 вимірювань величин X, Y і отримані результати Х=26,16; 26,75; 25,76; 26,44; 25,84; 25,52; 26,47; 26,39; 27,51 та У=16,11; 16,41; 15,29; 15,91; 15,71; 16,33; 16,32; 16,83; 16,29. Відомі середньоквадратичні відхилення (с. к. в.) похибок вимірювань цих величин:
виконані по 9 вимірювань величин X, Y і отримані результати Х=26,16; 26,75; 25,76; 26,44; 25,84; 25,52; 26,47; 26,39; 27,51 та У=16,11; 16,41; 15,29; 15,91; 15,71; 16,33; 16,32; 16,83; 16,29. Відомі середньоквадратичні відхилення (с. к. в.) похибок вимірювань цих величин:  Оцінити результат вимірювання U, вважаючи що результати вимірювань X,Y взаємно незалежні. Оцінити довірчі границі похибки вимірювання U з
Оцінити результат вимірювання U, вважаючи що результати вимірювань X,Y взаємно незалежні. Оцінити довірчі границі похибки вимірювання U з 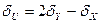 , А абсолютна похибка непрямого вимірювання (див. задачу3)
, А абсолютна похибка непрямого вимірювання (див. задачу3)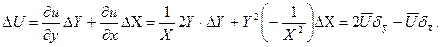
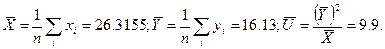
 тут
тут  - істинне, дійсне та середнє значення величини U, яку можна оцінити значеннями
- істинне, дійсне та середнє значення величини U, яку можна оцінити значеннями 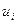 за прямими спостереженнями
за прямими спостереженнями 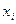 та
та  .
.

 та
та 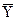 дорівнює сумі незміщеної оцінки дисперсії середнього випадкових спостережень та дисперсії інструментальної похибки відповідного вимірювального приладу, а саме:
дорівнює сумі незміщеної оцінки дисперсії середнього випадкових спостережень та дисперсії інструментальної похибки відповідного вимірювального приладу, а саме:



 та
та 

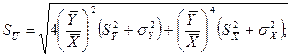

 . Звідси результат опосередкованого вимірювання
. Звідси результат опосередкованого вимірювання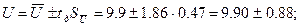


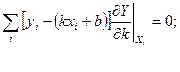

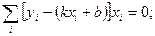




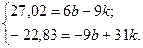

 ,
,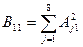 = 6,
= 6, = 5,
= 5, = 7,
= 7, = 5,
= 5, = 3,
= 3, = 5,
= 5, = 3,
= 3,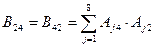 = 2,
= 2, = 3,
= 3, = 4,
= 4, = 14,13+8,17+9,13+7,26+7,19+2,15=48,03,
= 14,13+8,17+9,13+7,26+7,19+2,15=48,03, = 14,13+8,14+8,17+9,13+12,17 = 51,74,
= 14,13+8,14+8,17+9,13+12,17 = 51,74, = 14,13+8,14+6,15+9,13+7,26+7,19+2,1,5 = 54,15
= 14,13+8,14+6,15+9,13+7,26+7,19+2,1,5 = 54,15 = 14,13+6,15+7,26+7,19+12,17 = 46,9.
= 14,13+6,15+7,26+7,19+12,17 = 46,9. .
. .
. ,
, ,
,





