
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Реалізація методу простої ітерації за допомогою електронних таблицьСодержание книги
Поиск на нашем сайте
Спочатку згідно з методом треба замінити задане рівняння f (x) = 0 на еквівалентне х = φ(х). Існує універсальна заміна для функцій f (x), диференційовних на відрізку Висновок. Н айкраще (тобто найменше) можливе значення константи Ліпшиця функції φ(х) = х – λ f (x) на відрізку [ a;b ] ізоляції кореня рівняння f (x) = 0 дорівнює q = 1 – m1/М1, де М1 = Зауважимо, що монотонний збіг значно спрощує перевірку умови застосування методу простої ітерації (тобто умови Ліпшиця) та вибір його початкової точки x0. Справді, тоді всі наступні ітерації розташовані між коренем і x0, тому умову застосування достатньо перевірити на обраному відрізку ізоляції, а у якості x0 взяти будь – яку точку цього відрізку. У протилежному ж випадку, якщо корінь насправді розташований біля краю відрізка ізоляції, то наступна ітерація може опинитися за межами відрізку. Тому умову Ліпшиця слід перевіряти на відрізку втричі довше ніж відрізок ізоляції. Іноді замість φ(х) = х – λ f (x) використовують рівносильну заміну φ(х) = х – Нарешті значення М1 і m1 не важко знайти при умові, що функція f ′(x) монотонна на Отже, розглянемо застосування методу простої ітерації на такій задачі: розв‘язати рівняння f (x) = 2 ∙ sin x – x2 + 2 = 0 з точністю e = 0,5*10-5. 1. Відрізки ізоляції коренів рівняння f (x) = 0 уже визначені в першому розділі лекції і ці результати доведені комбінованим методом. Це [-1;-0,6] і [1,8;2,2]. 2. Знайдемо заміну φi(х) = х – λi f (x) для кожного з відрізків, i = 1,2. При i = 1 Аналогічно при i = 2 3. Знайдемо корені на відрізках ізоляції з точністю e = 0.5*10-5 методом простої ітерації за допомогою Excel. У першому випадку
Тут у А1 початкова точка а = – 1, у В1 формула функції f (x) при х = А1, у С1 значення λ1 ≈ 0,32, у А2 формула функції φ1(х) = х – λ1∙ f (x) при х = А1. Як і раніше, символ ↓ означає копіювання попередніх чарунок. В результаті отримаємо таку таблицю:
Як бачимо, починаючи з рядка 8 у стовбці А зміна значень припиняється. Це досягнуто з найбільшим числом значущих цифр, яке взагалі можливо при даному форматі чарунку. Як і для методу дихотомії, перевіримо правильність отриманого розв’язку безпосередньо. А саме надамо чарункам таких значень:
В результаті отримаємо:
У стовпці В відповідні значення функції f (x) приймаються автоматично. Оскільки f (-0,774980814 + 0,5*10-5) > 0, a f (-0,774980814 – 0,5*10-5) > 0, то значення – 0,77498 є коренем рівняння f (x) = 0 з точністю 0,5*10-5. Другий випадок є аналогічним:
В результаті отримаємо:
Зміна значень з максимальним можливим числом значущих цифр припиняється у рядку 12. Зробимо перевірку:
Тож значення 1,96188 є коренем рівняння f (x) = 0 з точністю 0,5*10-5. Спробуємо для
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 364; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.107.223 (0.006 с.) |

 ізоляції її кореня та з незмінним там знаком f′ (x) згідно з теоремою 1. А саме покладемо φ(х) = х – λ f (x), тут λ – деяка дійсна стала, λ ≠ 0. Підберемо l так, щоби у φ(х) на [ a;b ] була константа Ліпшиця q < 1. Звідси │φ′(х)│ =
ізоляції її кореня та з незмінним там знаком f′ (x) згідно з теоремою 1. А саме покладемо φ(х) = х – λ f (x), тут λ – деяка дійсна стала, λ ≠ 0. Підберемо l так, щоби у φ(х) на [ a;b ] була константа Ліпшиця q < 1. Звідси │φ′(х)│ = 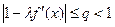 ;
;  або
або  , якщо додатково вважати, що φ′(х) ≥ 0, тобто що збіг ітерацій до кореня є монотонним (див. рисунок). Тому
, якщо додатково вважати, що φ′(х) ≥ 0, тобто що збіг ітерацій до кореня є монотонним (див. рисунок). Тому 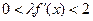 або
або  при φ′(х) ≥ 0. Тому, оскільки f′ (x) не змінює знак на
при φ′(х) ≥ 0. Тому, оскільки f′ (x) не змінює знак на  або ж │λ│≤ 1/М1 при φ′(х) ≥ 0. Бажано, щоби q було найменшим можливим: чим менше q, тим збіг швидше. При умові φ′(х) ≥ 0, тобто при
або ж │λ│≤ 1/М1 при φ′(х) ≥ 0. Бажано, щоби q було найменшим можливим: чим менше q, тим збіг швидше. При умові φ′(х) ≥ 0, тобто при  при кожному х буде найменшим можливим, якщо │λ│ обрати найбільшим можливим, тобто │λ│= 1/М1. Тоді найменше спільне для всіх х є
при кожному х буде найменшим можливим, якщо │λ│ обрати найбільшим можливим, тобто │λ│= 1/М1. Тоді найменше спільне для всіх х є  = 1 – m1/М1, де m1 =
= 1 – m1/М1, де m1 =  > 0. (2) Крім того при такому λ збіг ітерацій процесу хk = φ(хk-1) до кореня є монотонним.
> 0. (2) Крім того при такому λ збіг ітерацій процесу хk = φ(хk-1) до кореня є монотонним. , λ =
, λ =  , μ ≠ 0. Тоді відповідні необхідні умови на μ це
, μ ≠ 0. Тоді відповідні необхідні умови на μ це  і
і  , найкраща оцінка q досягається при μ = М1 =
, найкраща оцінка q досягається при μ = М1 = 


