
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інтерполювання за схемою ЕйткінаСодержание книги
Поиск на нашем сайте Якщо значення інтерполяційного многочлена треба обчислити лише в одній заданій точці, то немає потреби будувати самий многочлен. Звичайно для розв’язання такої задачі застосовують наступну інтерполяційну схему Ейткіна. Нехай функцію f (x), яка в точках xi набуває значень уi = f (xi) (і = 0, 1, …, n) задано таблично. Треба обчислити її значення в точці х є [x0; xn], яка не збігається з вузлами інтерполяції xi. Нехай L(k,k+1,…,i)(x) – це інтерполяційний многочлен з вузлами інтерполяції xk, xk+1,…, xi, зокрема L(k)(x) = f (xk). Має місце рівність L(k,k+1,…,i+1)(x) = Справді, права частина цієї рівності є многочленом степеня i – k + 1 і співпадає з f (x) у i – k + 2 точках xk, …, xi+1. Схема Ейткіна обчислення значення Ln(x) = L(0,1,…,n)(x) полягає у послідовних підрахунках за допомогою попередньої формули елементів наступної таблиці значень інтерполяційного многочлена.
Оцінка похибки значення Ln(x) заснована на теоремі 2. Згідно з пунктом 1 цієї теореми абсолютна похибка інтерполювання Rn(f,x) = f (x) – Ln(x) = f (х; x0; x1;…; xn)ωn+1(х); згідно з пунктом 2 Ln+1(x) – Ln(x) = f (x0; x1;…; xn+1)ωn+1(х). Нарешті згідно з пунктом 4, якщо функція f (x) n + 1 раз неперервно диференційовна, то f (х; x0; x1;…; xn) = Нехай вузли інтерполяції xi занумеровані в порядку зростання │xi – х│. Послідовно підраховують L0(x), L1(x), ε0, L2(x), ε1, …. Якщо при деякому m εm ≤ Е, де Е – точність, яка нас задовольняє, то підрахунки закінчуються і вважають, що f (x) ≈ Lm(x). Якщо нерівність εm ≤ Е не виконується при жодному m, то знаходять Задача. За схемою Ейткіна обчислити значення функції e2,72 з табличною точністю, якщо функція задана наступною таблицею. Обчислити це значення з точністю 10 вірних значущих цифр.
Розв’язання. Спочатку згідно з цією схемою перенумеруємо вузли інтерполяції xi в порядку зростання │х – xi│, де х = 2,72:
Побудуємо електронну таблицю для підрахунків за схемою Ейткіна (схожу на таблицю, яка була використана в попередньому параграфі). Надамо чарункам таких значень:
Тут у стовпці В значення х – xi, у стовпці С відповідні значення yi =
Оскільки ε0 = – 0,4422155, то отримане значення L1(2,72) = 15,20041 має тільки 2 вірні значущі цифри замість 6 потрібних. Тому зробимо другий крок схеми Ейткіна, як указано у наступній таблиці, а саме: 1) підрахуємо значення всіх многочленів другого степеня L(k,k+1)(x) при х = 2,72, просто скопіювавши формулу з D1 у діапазон D2:D7; 2) у чарунку E1 запишемо формулу для підрахунку L2(х) = L(0,1,2)(х) згідно з формулою (2); 3) знайдемо
у чарунці Е9 похибку ε1, просто скопіювавши формулу з D9. В результаті дістанемо:
Як бачимо, отримане значення L2(2,72) = 15,17913 має лише 3 вірні значущі цифри. Отже, потрібним є третій крок схеми: 1) скопіюємо з Е1 у діапазон Е2:Е6, підрахувавши тим
самим значення всіх многочленів третього степеня L(k,k+1,k+2)(x) при х = 2,72; 2) у чарунку F1 запишемо формулу для підрахунку L3(х) = L(0,1,2,3)(х) згідно з (2); 3) скопіюємо формулу з Е9 у F9, тим самим підрахувавши похибку ε2. В результаті дістанемо:
Тут уже L3(х) = 15,18024 має 4 вірні значущі цифри, тобто потрібен ще крок. Зазначимо, що формула у чарунку F1 введена дещо по – іншому: адреса стовпця В тут є абсолютною. Якщо тепер скопіювати цю формулу у G1, то за правилами копіювання у Excel дістанемо G1 = (F2*$B4 – F1*$B2)/($B1 – $B4). Насправді ж згідно з (2) формула для підрахунку L4(х) = L(0,1,2,3,4)(х) виглядає так: G1 = (F2*$B5 – F1*$B2)/($B1 – $B5). Отже, достатньо для отримання правильної формули після копіювання виділити чарунку G1, підвести курсор у рядок формул Excel і виправити у відповідній формулі 4 на 5. Решта дій на четвертому кроці та ж сама:
В результаті отримаємо:
Отримане значення L4(х) = 15,18033 тепер має 6 вірних значущих цифр, що відповідає точності табличних даних: отже, це відповідь на перше питання. Для обчислення f (2,72) = e2,72 з точністю 10-10 необхідні ще кроки, які ми проведемо так само, як і попередній:
У чарунці H1 треба після копіювання виправити у відповідній формулі 5 на 6. В результаті
Значення L5(х) = 15,18032 уже має всі 7 вірних значущих цифр. Максимально можна ще зробити 2 кроки так само, як попередні, і отримати значення L7(х):
Отже, значення L7(х) має 9 вірних значущих цифр. Щоби їх побачити треба розсунути стовпець J, маємо L7(х) ≈ 15,1803222. Досягти 10 вірних значущих цифр принципово не можливо при даних задачі. Тому за схемою Ейткіна вважаємо, що e2,72 ≈ 15,1803222 з оцінкою похибки ε6 = 4,5E-08. Задачу закінчено. Зазначимо, що як вибір кількості n вузлів інтерполювання, так і спосіб їх упорядкування насправді не є оптимальними. Як видно з теореми 1, похибка інтерполяції Rn(f, x) = f (x) – Ln(x) = ξk =
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 414; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.006 с.) |

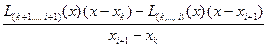 (2).
(2). , де min{x0;x1;…;xn} ≤ ξ ≤ max{x0;x1;…;xn}. Звідси, якщо величини │xi – х│ достатньо малі, то f (х; x0; x1;…; xn) ≈
, де min{x0;x1;…;xn} ≤ ξ ≤ max{x0;x1;…;xn}. Звідси, якщо величини │xi – х│ достатньо малі, то f (х; x0; x1;…; xn) ≈  ≈ f (x0; x1;…; xn+1). Отже, Ln+1(x) – Ln(x) ≈ f (x) – Ln(x) = Rn(f,x). Тому величину εm = Lm+1(x) – Lm(x) можна розглядати, як наближену оцінку абсолютної похибки Rm(f,x) інтерполяційної формули f (x) ≈ Lm(x). Не важко довести, що заміна Rm(f,x) на εm = Lm+1(x) – Lm(x) є тут коректною за умови, що │
≈ f (x0; x1;…; xn+1). Отже, Ln+1(x) – Ln(x) ≈ f (x) – Ln(x) = Rn(f,x). Тому величину εm = Lm+1(x) – Lm(x) можна розглядати, як наближену оцінку абсолютної похибки Rm(f,x) інтерполяційної формули f (x) ≈ Lm(x). Не важко довести, що заміна Rm(f,x) на εm = Lm+1(x) – Lm(x) є тут коректною за умови, що │ 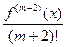 ωm+1(х)│< │εm│.
ωm+1(х)│< │εm│.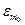 =
= 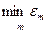 і вважають, що f (x) ≈
і вважають, що f (x) ≈ 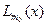 з оцінкою похибки
з оцінкою похибки  = f (xi) = L(i)(x). У чарунці D1 формула визначає L1(х) = L(0,1)(х) згідно з формулою (2). У чарунці D9 обчислюємо похибку ε0. В результаті дістанемо:
= f (xi) = L(i)(x). У чарунці D1 формула визначає L1(х) = L(0,1)(х) згідно з формулою (2). У чарунці D9 обчислюємо похибку ε0. В результаті дістанемо: має найменше значення, якщо вузлами інтерполювання є числа хk =
має найменше значення, якщо вузлами інтерполювання є числа хk = 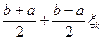 , де
, де (k = 0,1,…,n) – це нулі так званого многочлена Чебишова Tn+1(t), Tn+1(t) = cos((n+1)arccos t). Вони дійсні, різні, належать (– 1; 1) і згущаються біля кінців інтервалу із зростанням n. За такого вибору вузлів │ωn+1(х)│ ≤ 2
(k = 0,1,…,n) – це нулі так званого многочлена Чебишова Tn+1(t), Tn+1(t) = cos((n+1)arccos t). Вони дійсні, різні, належать (– 1; 1) і згущаються біля кінців інтервалу із зростанням n. За такого вибору вузлів │ωn+1(х)│ ≤ 2 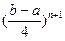 . Проте навіть звідси не випливає, що при достатньо малому b – a абсолютна похибка інтерполяції Rn(f,x) буде збігатися до нуля із зростанням n.
. Проте навіть звідси не випливає, що при достатньо малому b – a абсолютна похибка інтерполяції Rn(f,x) буде збігатися до нуля із зростанням n.


