
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптимізаційні задачі. Математичне програмуванняСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Нехай f (x) – функція n змінних, визначена на множині V Означення 1. Оптимальним розв’язком задачі (f, V, Ω) називається таке х0 є Ω, що f (x0) ≤ f (x) (або f (x0) ≥ f (x)) для всіх х є Ω. Оптимізаційну задачу називають нерозв’язною, якщо вона не має оптимальних розв’язків. Розв’язати оптимізаційну задачу означає або знайти всі її оптимальні розв’язки, або ж довести її нерозв’язність. Зокрема, задача мінімізації (максимізації) (f, V, Ω) буде нерозв’язною, якщо f (x) не обмежена знизу (зверху) на допустимій множині Ω. Методи розв’язування оптимізаційної задачі (f, V, Ω) часто називають методами математичного програмування. Сам термін програмування в цьому випадку зумовлений тим, що саме математичне програмування є підґрунтям мікроекономіки – одної з двох найважливіших складових економічної науки і шуканою у таких задачах насправді є деяка програма дій. Необхідною передумовою будь – якого використання методів обчислень є створення математичної моделі досліджуваного об’єкта чи явища. Першим кроком при розв’язуванні задач економіки є побудова їх економіко – математичної моделі, тобто такої математичної задачі, до розв’язання якої зводиться поставлена економічна задача. Розглянемо деякі приклади. 1. Для виготовлення продукції двох типів (А і Б) на заводі використовують сировину трьох видів (1, 2 и 3). Для виробництва кожного виробу типу А витрачається 10 одиниць сировини виду 1, 20 одиниць виду 2 і 15 виду 3; для кожного виробу типу Б – 20, 10 и 15 відповідно. Запаси сировини складають: 1 виду 100 одиниць, 2 виду – 100, 3 виду – 90. Скласти щоденний план виробництва, що забезпечує найбільший прибуток, якщо кожний виріб типу А дає 200 гривен прибутку, Б – 300 гривен. Зручно дані поставленої задачі сформувати у наступну таблицю.
Побудуємо математичну модель цієї задачі. Позначимо через хА та хБ кількість одиниць продукції А і Б відповідно, яку передбачається виготовити по плану. За умовою задачі цільова функція f – прибуток, який треба максимізувати: f = 200хА + 300хБ. При цьому сировини 1 буде витрачено 10хА + 20хБ. Кількість витраченої сировини не може перевищувати її запасу, тому 10хА + 20хБ ≤ 100. Аналогічно для сировини 2 20хА + 10хБ ≤ 100, для сировини 3 15хА + 15хБ ≤ 90. Змінні хА і хБ повинні бути невід’ємними, оскільки це кількості продукції. Отже економіко – математична модель формулюється так: треба знайти такі значення змінних хА та хБ , за яких задовольняється система нерівностей
і цільова функція f = 200 хА + 300 хБ набуває найбільшого можливого значення. Знайти такі хА та хБ і означає знайти план виробництва. Це простіший приклад задачі планування виробництва, яка найбільш традиційно формулюється так у загальному вигляді. Підприємство виробляє деяку однорідну продукцію і використовує для цього n різних технологічних засобів і m різних ресурсів. За одиницю часу використання j – го технологічного засобу виготовляється сj одиниць продукції, при цьому витрати і – го ресурсу a ij одиниць (і = 1, 2, …, m, j = 1, 2, …, n). Треба так спланувати роботу підприємства, щоби кількість продукції була найбільшою при умові, що витрати і – го ресурсу не можуть перебільшувати bi одиниць (і = 1, 2, …, m). Нехай хj ≥ 0 (j = 1, 2, …, n) – час використання підприємством j – го технологічного засобу. Замість прибутку у попередньому прикладі тут цільова функція f – це кількість виробленої продукції: f =
і цільова функція f = 2. Задача про раціон. У господарстві є два вида кормів вартістю 20 та 30 гривен за одиницю корму відповідно. У першому кормі міститься 2 одиниці вітаміну А та 3 одиниці вітаміну В, у другому 5 одиниць А та 2 одиниці В. Раціон повинен містити не менш як 9 одиниць А та 8 одиниць В. Скласти найдешевший раціон, який задовольняє цим вимогам. Через хА і хВ позначимо відповідно кількість першого і другого кормів у раціоні. Тут цільова функція f – це вартість раціону: f = 20хА + 30хВ. За таким планом раціон містить 2хА + 5хВ одиниць вітаміну А, за вимогою задачі 2хА + 5хВ ≥ 9. Аналогічно для вітаміну В 3хА + 2хВ ≥ 8. Змінні хА і хВ повинні бути невід’ємними, оскільки це кількості продукції. Отже математична модель формулюється так: треба знайти такі значення змінних хА та хВ , за яких задовольняється система нерівностей
і цільова функція f = 20хА + 30хВ набуває найменшого можливого значення. У загальному вигляді задача про раціон традиційно формулюється так. У господарстві є n різних кормів, кожен з яких містить m різних поживних речовин. Відомо, що одиниця j – го корму коштує сj грошових одиниць (j = 1, 2, …, n) і містить a ij одиниць і – ої поживної речовини (і = 1, 2, …, m). Треба скласти раціон так, щоб він задовольняв мінімальну потребу bi (і = 1, 2, …, m) у кожній речовині при найменшій вартості раціону. Позначимо кількість j – го корму в раціоні через хj ≥ 0 (j = 1, 2, …, n), цільова функція f – це вартість раціону: f =
і цільова функція f = 3. Транспортна задача. Нехай з трьох пунктів відправлення Р1, Р2, Р3 треба перевезти однорідний вантаж до трьох пунктів призначення М1, М2, М3, в тому числі з пункту Р1 – 12 т, з пункту Р2 – 8 т, з пункту Р3 – 10 т. Вантаж повинен надійти за призначенням у пункт М1 – 6 т, пункт М2 – 9 т, пункт М3 – 15 т. Вартість перевезення тони вантажу з пункту Рi до пункту Мj (i, j = 1,2,3) наведена у наступній таблиці.
Треба, щоби весь вантаж був вивезений з пунктів відправлення, повністю був задоволений попит пунктів призначення і загальна вартість перевезень була мінімальною. Побудуємо математичну модель цієї задачі. Позначимо через хij вагу вантажу (в тонах), запланованого для перевезення з пункту Рi до пункту Мj (i, j = 1,2,3). Вартість перевезення багажу дорівнює f = х11 + 3х12 + 4х13 + 2х21 + 5х22 + 3х23 + 6х31 + 7х32 + 4х33 – цільова функція задачі. Весь вантаж буде вивезений з пунктів відправлення, якщо х11 + х12 + х13 = 12, х21 + х22 + х23 = 8, х31 + х32 + х33 = 10. Попит пунктів призначення буде повністю задоволений, якщо х11 + х21 + х31 = 6, х12 + х22 + х32 = 9, х13 + х23 + х33 = 15. Отже, серед невід’ємних розв’язків системи
треба знайти такий, за якого функція f набуває найменшого значення. У загальному випадку транспортну задачу звичайно формулюють так. Нехай однорідний вантаж, що знаходиться у m постачальників у кількості а i (і = 1, 2, …, m) одиниць відповідно, треба перевезти n споживачам у кількості bj (j = 1, 2, …, n) одиниць. Вартість перевезення одиниці вантажу від і – го постачальника до j – го споживача становить сij одиниць. Спланувати перевезення вантажу так, щоби весь вантаж був вивезений від постачальників, повністю був задоволений попит споживачів і вартість перевезень була мінімальною. Позначимо через хij кількість одиниць вантажу, запланованого для перевезення від постачальника і до споживача j. Математична модель транспортної задачі має такий вигляд. Знайти найменше значення функції f =
У всіх наведених прикладах цільова функція f є лінійною, а множина допустимих розв’язків оптимізаційної задачі визначається системою лінійних рівнянь і нерівностей. Означення 2. Оптимізаційна задача (f, V, Ω), у якій цільова функція f є лінійною на V, а Ω є множиною розв’язків деякої системи лінійних рівнянь і нерівностей називають задачею лінійного програмування. Систему лінійних рівнянь і нерівностей, яка визначає Ω, називають системою обмежень задачі лінійного програмування.
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 974; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.01 с.) |

 Rn, підмножина Ω
Rn, підмножина Ω 
 ; все інше так само, лише у загальному вигляді. За планом буде витрачено
; все інше так само, лише у загальному вигляді. За планом буде витрачено 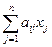 одиниць і–го ресурсу. Звідси
одиниць і–го ресурсу. Звідси 




 за обмежень
за обмежень



