
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Загальна характеристика методів розв’язування задач нелінійного програмування.Содержание книги
Поиск на нашем сайте Під час моделювання реальних економічних процесів слід враховувати складні й переважно нелінійні взаємозв’язки між параметрами досліджуваних систем. Методи розв’язування задач оптимізації із нелінійними цільовими функціями й нелінійними обмеженнями розглядаються у спеціальному розділі математичного програмування –нелінійному програмуванні. До типових сфер його застосування можна віднести задачі планування й управління промисловим виробництвом, товарними ресурсами й капіталовкладеннями, в яких передбачається, що ефективність виробництва або використання ресурсів змінюється не пропорційно до його обсягів. Наприклад, у задачах транспортного типу вартість перевезень одиниці вантажу часто має значні коливання залежно від обсягу транспортування. Математична модель задачі нелінійного програмування (НЛП) має такий вигляд:
У загальному випадку цільова функція задачі і /або/ функції і системи обмежень можуть бути нелінійними відносно змінних Для розв’язування задач нелінійного програмування не існує єдиного універсального методу, аналогічного до симплексного методу в лінійному програмуванні. Підходи до пошуку методів розв’язування задач НЛП визначаються типами нелінійних залежностей і обмежень задачі. Істотно, що в цих задачах область допустимих розв’язків не завжди є опуклою, а точка оптимуму, на відміну від випадку лінійного програмування, може бути не лише кутовою, а й міститися на межі або всередині даної області. Широка сукупність методів розв’язування задач нелінійного програмування базується на використанні диференційного числення для знаходження точок екстремумів функцій. Сутність згаданих щойно методів розв’язування нелінійних задач розкриємо в межах їх класифікації, згідно з якою вирізняють такі методи: 1) класичної математики знаходження екстремумів функцій; 2) для задач з обмеженнями-рівностями; 3) для задач з обмеженнями-нерівностями. Методи першої групи грунтуються на дослідженнях необхідних і достатніх умов існування екстремумів функцій з використанням їх частинних похідних першого і другого порядків. Це означає, що всі міркування виконуються за припущення про неперервність та диференційованість, а також відсутність умов невід’ємності і цілочисельності змінних задачі. До методів другої групи можна віднести метод зведеного градієнта (метод Якобі), який є узагальненням симплексного методу лінійного програмування, а також найпоширеніший метод множників Лангранжа, який докладніше буде розглянуто далі. Методи третьої групи переважно базуються на використання умов Куна-Таккера (метод Франка-Вульфа) існування екстремумів функцій. Але в загальному випадку для задач цього типу не можна сформулювати достатніх умов існування екстремуму, через що не можна точно визначити тип знайденого оптимуму, тобто встановити, який він – локальний чи глобальний. Тому використання даних умов є найефективнішим для задач з опуклими цільовими функціями, оскільки будь-який їх локальний екстремум є одночасно і глобальним. Кожний з градієнтних методів розв’язування нелінійних задач з обмеженнями у вигляді нерівностей являє собою ітеративний процес послідовних наближень, в результаті якого формується послідовність точок –розв’язків задачі у напрямі найшвидшого зростання (спадання) цільової функції. Нагадаємо, що градієнтом функції є вектор її частинних похідних у певній точці, який визначає напрям і швидкість зростання функції. Істотно, що оптимум задачі, який знайдено градієнтними методами, є лише локальним. Для розв’язування деяких класів задач нелінійного програмування застосовуються методи, які передбачають певний вид цільової функції. Так, для задач з опуклими цільовими функціями у вигляді квадратичної форми
використовуються методи квадратичного програмування, які ґрунтуються на теоремі Куна-Таккера про існування екстремуму функції Лагранжа для досліджуваної задачі. Нехай цільова функція задачі як функція багатьох змінних є сепарабельною, тобто її можна подати у вигляді алгебраїчної суми однорідних функцій відносно однієї змінної (аргументу):
Тоді наближені екстремуми функцій визначаються методами лінійно-кускової апроксимації. Їх основна ідея полягає в кусково-лінійній апроксимації початкової нелінійної функції лінійними залежностями, які розглядаються для кожної складової сепарабельної функції в інтервалах, що визначені точками сітки. Досліджуючи зміни цих функцій на кінцях інтервалів, можна перетворити початкову нелінійну задачу на задачу лінійного програмування, яка оперує з приростами цільової функцій та обмежень.
Метод множників Лагранжа. Сутність методу полягає в перетворенні початкової задачі пошуку умовного екстремуму цільової функції на задачу знаходження безумовного екстремуму деякої відповідним чином побудованої функції Лангранжа. Розв’язується загальна задача нелінійного програмування (3.1) – (3.2) за припущення, що система обмежень містить лише рівняння, а функції
Розв’язувати задачу НЛП починаємо з побудови функції Лагранжа. Щоб побудувати функцію Лагранжа, вводимо сукупність змінних
Для визначення безумовного екстремуму цієї функції (згідно з необхідною умовою його існування) слід знайти частинні похідні від функції Лагранжа по всіх n+m змінних Прирівнявши ці похідні до нуля, маємо таку систему рівнянь:
Будь-який розв’язок цієї системи визначає точку Приклад 3.1. Д ля виробництва двох видів продукції А і В використовуються два типи обмежених ресурсів. Прибуток від реалізації цих виробів є нелінійною функцією від обсягів виробництва. Вихідні дані щодо норм витрат ресурсів на одиницю продукції, запасу ресурсів у виробника, а також прибутку за одиницю продукції в табл. 3.1.
Таблиця 3.1.
За припущення, що запас ресурсів необхідно використати повністю, визначити обсяги виробництва продукції А і В, за яких сумарний прибуток від їх реалізації досягатиме екстремального значення. Розв’язування. Математична модель цієї задачі нелінійного програмування така:
за умов Для знаходження точки умовного екстремуму цільової функції побудуємо функцію Лагранжа:
Знайдемо частинні похідні від цієї функції за всіма невідомими параметрами:
Розв’язавши цю систему рівнянь, отримаємо:
Отже, точка екстремуму для функції сумарного прибутку Z є Для визначення типу екстремуму (Zmax або Zmin) необхідно дослідити другу похідну функції Лагранжа в стандартній точці Приклад 3.2. Знайти оптимальне рішення нелінійної задачі методом множників Лагранжа.
при обмеженні Складемо функцію Лагранжа:
Візьмемо похідні від функції Лагранжа:
Отримали три рівняння з трьома невідомими, з яких з третього рівняння випливає: X1=8–X2 (3.3) Підставляємо (3.3) у перше рівняння і вирішуємо далі сумісно з другим:
Таким чином, отримуємо оптимальне значення функції мети:
при обмеженні Після цього досліджують оптимум 1) 2) Тоді робимо висновок: у точці
3.3. Задачі для самостійного розв’язання: №1. Розв’язати такі задачі квадратичного програмування. 1. Z = – X1 – 2X2 + X22 а Min; 2. Z = - 8X1 - 10X2 + X12 + X22 а Min; 3X1 +2X2 < 6+A X1 +2X2 < 4 +A, 3X1 + 2X2 + X3 = 6 +A, X1 > 0, X2 > 0. X1 > 0, X2 > 0, X3 > 0. 2. Z = 3X1 –3X2 – X12 – 3X22 а Max; 4. Z = 2X1X2 – X12 – X22 а Max; 3X1 +X2 +X3 +X4 = 16+A, 2X1 – X2 < 6 +A, – X1 + 3X2 –X3 –X4 = 4 +A, X1 + 2X2 <10+ A, X1 > 0, X2 > 0, X3 > 0, X4 > 0. X1 > 0, X2 > 0. №2. Розв’язати задачу нелінійного програмування методом множників Лагранжа. Z = 3X1 – 3X2 – X12 – 3X22 à Max; 3X1 +X2 = 16, – X1 + 3X2= 4, X1 > 0, X2 > 0. №3. Розв’язати задачу нелінійного програмування методом множників Лагранжа. Z = 2X1X2 – X12 – X22 à Max; 2X1 – X2 = 6, 3X1 + 2X2 = 10, X1 > 0, X2 > 0. №4. Розв’язати задачу нелінійного програмування методом множників Лагранжа. Z = (X1 + X2)2 à Min; X1 + 7 X2 = 2; X1 + 2X2= 6; X1 > 0, X2 > 0. №5. Розв’язати задачу нелінійного програмування методом множників Лагранжа. Z = (5X1 + 3X2)2 à Min; 2X1 + 5 X2 = 9; 3X1 + 4X2= 15; X1 > 0, X2 > 0. №6. Розв’язати задачу нелінійного програмування методом множників Лагранжа. Z = 7X12 + 3X22 à Max; 4X1 – 5 X2 = 9; X1 + 5X2= 15; X1 > 0, X2 > 0.
№7. Методом множників Лагранжа розв’язати задачі. 1. F=(4X1–N)2 + (X2 –3N)à min; 2. F=(X1–A)2 + (3X2 – N)2à min 3X1 + AX2=N; 6X1 + 3X2=N Тут N – порядковий номер студента у групі. А= №8. Методом множників Лагранжа розв’язати задачі.
ТЕСТИ 1. Точка а) дотику б) сідловою в) локального або глобального екстремуму функції Z г) цільового призначення 2. Опукле програмування – це: а) розділ математичного програмування, який вивчає методи розв'язання задач цілеспрямованого характеру б) розділ математичного програмування, в якому вивчаються методи відшукання максимуму опуклої, або мінімуму увігнутої функції на опуклій множині
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 734; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

 (3.1) за умов обмежень
(3.1) за умов обмежень (3.2)
(3.2) Отже, задача лінійного програмування є окремим випадком щойно розглянутої задачі.
Отже, задача лінійного програмування є окремим випадком щойно розглянутої задачі.
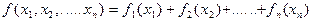
 неперервні і диференційовані, тобто:
неперервні і диференційовані, тобто: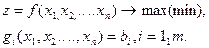
 , які називаються множниками Лагранжа. Тоді функція Лагранжа набирає вигляду:
, які називаються множниками Лагранжа. Тоді функція Лагранжа набирає вигляду:
 та
та  .
. ;
;
 яка є екстремальною для цільової функції Z.
яка є екстремальною для цільової функції Z.


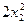
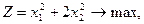



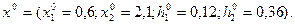
 , яка визначає обсяги виробництва продукції А і В у кількості відповідно 0,6 та 2,1 одиниці.
, яка визначає обсяги виробництва продукції А і В у кількості відповідно 0,6 та 2,1 одиниці.
 .
.
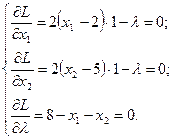
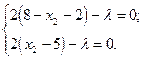




 ,
, .
. на мінімум та максимум. Для цього збільшуємо та зменшуємо змінну
на мінімум та максимум. Для цього збільшуємо та зменшуємо змінну  :
: Але ми повинні врахувати обмеження (8.3), з якого випливає
Але ми повинні врахувати обмеження (8.3), з якого випливає  . Тоді
. Тоді  — функція мети збільшилась.
— функція мети збільшилась. З врахуванням обмеження (8.3) отримуємо
З врахуванням обмеження (8.3) отримуємо  і тоді
і тоді  — функція мети збільшилась.
— функція мети збільшилась. ;
;  отриманий мінімум функції мети і остаточно
отриманий мінімум функції мети і остаточно .
.






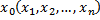 , в якій функція
, в якій функція  , досягає свого глобального або локального екстремуму при додатковій умові, що точка
, досягає свого глобального або локального екстремуму при додатковій умові, що точка  задовольняє рівняння
задовольняє рівняння  , зветься точкою:
, зветься точкою:


