
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. Складання математичних моделей задач лінійного програмуванняСодержание книги
Поиск на нашем сайте Загальне завдання для перелічених нижче задач має такий вигляд: скласти математичні моделі задач лінійного програмування; отримати рішення графо-аналітичним методом; дати рекомендації щодо виробництва виробів. У наведених нижче задачах мається на увазі, що: § Кожний студент по можливості повинен отримати індівідуальне завдання. З цією метою використовуються такі позначення: § Математична модель складається і розв’язується студентом на практичних заняттях. При цьому можливі два варіанти видачі завдань. Згідно з першим варіантом студент самостійно задає об’єм наявних ресурсів та норми витрат ресурсів на виробництво товарів. Згідно з другим – видає викладач, користуючись наведеними нижче таблицями. § Одиниці вимірювання ресурсів та норм витрат вважаються однаковими (наприклад: кг; метр; бочка, пачка, комплект, тюк, лист визначеного типу; м2; літр; м3; “у.о.” – умовна одиниця та ін.), а норми витрат відносяться до одного виробу (“кг/1 шт.”, “бочка визначеного типу/1 шт” і т.д.). Тому не вказуються розмірності норм витрат та ресурсів. Іноді в задачах використовується визначення “у.о.” – “умовні одиниці”. Під трудовими ресурсами розглядаються обмеження, пов’язані з витратою часу робітниками на виробництво продукції; трудові ресурси вимірюються у “л.г.” – людино-годинах, а відповідні норми – у “л.г./одиницю виробу”. § Наявні ресурси, норми витрат ресурсів на один виріб та ускладнення, які вводяться у задачі, повинні розглядатись як умовні величини та обмеження, які часто використовуються лише для ускладнення задачі з метою кращого опанування студентами методу лінійного програмування та зручності графічного розв’язання задачі. Тобто задачі розглядаються як навчальні. Треба також враховувати, що для кожного підприємства вказані величини є індивідуальними. § Гроші як ресурси витрачаються на інші невказані додаткові ресурси (наприклад під час виготовлення страв – на невказані компоненти: спеції, овочі; виготовлення радіоприймачів – на конденсатори, резистори, друковані плати; виготовлення одягу та взуття – на нитки, клей та ін.). Гроші також можуть використовуватись з метою спрощення задач (для вилучення з розгляду другорядних, не основних, численних ресурсів, які не впливають суттєво на процеси, але водночас є необхідним компонентом). § Завдання можуть ускладнюватись такими додатковими вимогами: обмеженням по мінімуму, за якого виробництво ще є рентабельним (наприклад, X1>N; Х1+Х2>2N); обмеженням по максимуму, пов’язаному з максимальною виробничою потужністю підприємства (наприклад, X1<30N; X1+X2<50N); плановими обмеженнями (наприклад, X1/X2=А; X1>100N; X1<250N; X1+X2>20A); вимогами ринку (наприклад, X1/X2=A; X1=(120–250)N); обмеженнями по комплектації (наприклад, X1=A*X2); вимогами визначення мінімальної кількості ресурсу, який потрібно додатково закупити, щоб збільшити випуск продукції; вимогами розрахунку функції мети у кожній кутовій точці та по межах багатокутника отриманого графічного рішення та ін. § Завдання можуть ускладнюватись викладачем навмисними суперечностями, щоб привчити до реальних умов складання математичних моделей. Наприклад: отриманий план по випуску продукції X1/X2=4 N може суперечити даним попиту на ринку X1/X2=3N (студент повинен прийняти рішення: поставити до відома керівництво, орієнтуватись на задоволення вимог ринку); або одне рівняння повторює інше; або математична модель не має рішення та ін. § Завдання можуть ускладнюватись елементами стохастичного програмування. При цьому задача повинна зводитись до задач ЛП. Наприклад, якщо у обмеженні А1Х1+А2Х2 § Кожне завдання завершується рекомендаціями (бо рішення приймає людина), у яких вказується: значення функції мети, кількість виробленої продукції, залишки ресурсів.
|
||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 262; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |

 – порядковий номер студента у групі;
– порядковий номер студента у групі;  .
. BJ наявний ресурс є випадковою величиною з рівномірним розподілом у межах BJ=(BJ1–BJ2)=(100–120) кг, то значення змінних XJ (кількість продукції, що випускається) за ймовірності Р=0,8 у забезпеченні наявності потрібних ресурсів розраховується з використанням конкретного значення ресурсу BJ= BJ1+(BJ2–BJ1)(1–Р)= 100 + (120-100)(1–0,8)=104 кг, тобто задача зводиться до задачі ЛП. У обмеженні А1Х1+А2Х2
BJ наявний ресурс є випадковою величиною з рівномірним розподілом у межах BJ=(BJ1–BJ2)=(100–120) кг, то значення змінних XJ (кількість продукції, що випускається) за ймовірності Р=0,8 у забезпеченні наявності потрібних ресурсів розраховується з використанням конкретного значення ресурсу BJ= BJ1+(BJ2–BJ1)(1–Р)= 100 + (120-100)(1–0,8)=104 кг, тобто задача зводиться до задачі ЛП. У обмеженні А1Х1+А2Х2 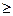 BJ (за ймовірності Р=0,8 у забезпеченні даної нерівності щодо наявного ресурсу) значення ресурсу BJ= BJ1+(BJ2–BJ1)Р=100 + (120–100)0,8=116 кг.
BJ (за ймовірності Р=0,8 у забезпеченні даної нерівності щодо наявного ресурсу) значення ресурсу BJ= BJ1+(BJ2–BJ1)Р=100 + (120–100)0,8=116 кг.


