
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4. Коротка характеристика моделей управління запасамиСодержание книги
Поиск на нашем сайте 1.1. Модель оптимального розміру замовлення. Передумови: 1) темп попиту на товар відомий і постійний; 2) отримання замовлення миттєве; 3) відсутні кількісні знижки при закупівлі великих партій товару; 4) єдині змінні параметри – витрати замовлення і зберігання; 5) виключається дефіцит у разі своєчасного замовлення. Початкові дані: темп попиту; витрати замовлення і зберігання. Результат: оптимальний розмір замовлення; час між замовленнями і їх кількість за період. 1.2. Модель оптимального розміру замовлення полягає у припущенні, що отримання замовлення не миттєве. Отже, потрібно знайти об'єм запасів, при якому необхідно робити нове замовлення. Початкові дані: темп попиту; витрати замовлення і зберігання; час виконання замовлення. Результат: оптимальний розмір замовлення; час між замовленнями; точка відновлення запасу. 1.3. Модель оптимального розміру замовлення полягає у припущенні, що допускається дефіцит продукту і пов'язаний з ним упущений прибуток. Необхідно знайти точку відновлення. Початкові дані: темп попиту; витрати замовлення і зберігання; упущений прибуток. Результат: оптимальний розмір замовлення; час між замовленнями; точка відновлення запасу. 1.4. Модель з урахуванням виробництва (у поєднанні з умовами 1.1 – 1.3). Необхідно розглядати рівень щоденного виробництва і рівень щоденного попиту. Початкові дані: темп попиту; витрати замовлення і зберігання; упущений прибуток; темп виробництва. Результат: оптимальний рівень запасів (точка відновлення) 1.5. Модель з кількісними знижками. З'являється можливість кількісних знижок залежно від розміру замовлення. Розглядається залежність витрат зберігання від ціни товару. Оптимальний рівень замовлення визначається виходячи з умови мінімізації загальних витрат для кожного виду знижок.
Модель 1.1 Найекономічніші розміри замовлення. Замовлення, що поповнює запаси, надходить як одна партія. Рівень запасів убуває з постійною інтенсивністю поки не досягне нуля. У цій точціі надходить замовлення, розмір якого рівний Q, і рівень запасів відновлюється до максимального значення. При цьому оптимальним рішенням задачі буде той розмір замовлення, при якому мінімізуються загальні витрати за період (рис. 4.1).
рис. 4.1 Нехай Q – розмір замовлення; Т – протяжність періоду планування; D – величина попиту за період планування; d – величина попиту на одиницю часу; До – витрати замовлення; H – питомі витрати за період; h – питомі витрати зберігання за одиницю часу. Тоді: сукупні витрати замовлення
сукупні витрати зберігання
оптимальний розмір замовлення; оптимальне число замовлень за період; час циклу (оптимальний час між замовленням).
Модель 1.2. Введемо припущення про те, що замовлення може бути одержано не миттєво, а з часом. Тоді нам необхідно наперед робити замовлення, щоб в потрібний час мати достатню кількість товару на складі. Отже, нам необхідно знайти той рівень запасів, при якому робиться нове замовлення. Цей рівень називається точкою відновлення R. Хай L – час виконання замовлення. Тоді R = величина попиту в одиницю часу, помножена на час виконання замовлення =. Інші характеристики системи визначаються також, як і в модели1.1. Модель ілюструється рис. 4.2.
рис. 4.2 Приклад 1. Андрій Удачливий є торговим агентом компанії TOYOTA і займається продажем останньої моделі цієї марки автомобіля. Річний попит оцінюється в 4000 од. Ціна кожного автомобіля 90 тис. у.о., а річні витрати зберігання складають 10% від ціни самого автомобіля. Андрій зробив аналіз витрат замовлення і зрозумів, що середні витрати замовлення складають 25 тис. у.о. на замовлення. Час виконання замовлення рівний восьми дням. Протягом цього часу щоденний попит на автомобілі рівний 20. - Чому дорівнює оптимальний розмір замовлення? - Чому дорівнює точка відновлення? - Які сукупні витрати? - Яка оптимальна кількість замовлень в рік? - Який оптимальний час між двома замовленнями, якщо припустити, що кількість робочих днів у році дорівнює 200? Початкові дані величина попиту за рік D = 4000; витрати замовлення До = 25; витрати зберігання h =; ціна за одиницю з = 90; час виконання замовлення L = 8; щоденний попит d = 20; число робочих днів T = 200. Розв’язання: оптимальний розмір замовлення
точка відновлення R = 160 – 149 = 11; число замовлень за рік
сукупні витрати = сукупні витрати замовлення + сукупні витрати зберігання
вартість продажів = 360000; число днів між замовленнями t = 7,45.
Модель 1.3. О птимальні розміри замовлення в припущенні, що допускається дефіцит продукту і пов'язаний з ним упущений прибуток (рис. 4.3).
рис. 4.3 Нехай p – упущений прибуток в одиницю часу, що виникає в результаті дефіциту однієї одиниці продукту; P – упущений прибуток за період, що виникає в результаті дефіциту однієї одиниці продукту. Тоді: оптимальний розмір замовлення
максимальний розмір запасу
максимальний дефіцит.
Модель 1.4 Виробництва і розподілу. У попередній моделі ми допускали, що поповнення запасу відбувається одноразово. Але в деяких випадках, особливо в промисловому виробництві, для комплектування партії товарів потрібен значний час і виробництво товарів для поповнення запасів відбувається одночасно із задоволенням попиту. Такий випадок показаний на
рис. 4.4.
рис. 4.4 Попит і виробництво є частиною циклу відновлення запасів. Нехай u - рівень виробництва в одиницю часу; До – фіксовані витрати зберігання. Тоді сукупні витрати зберігання дорівнюють: середній рівеньзапасів середній рівень запасів = (максимальний рівень запасів)/2; максимальний рівень запасів дорівнює
час виконання замовлення
витрати замовлення дорівнює
оптимальний розмір замовлення
максимальний рівень запасів
Модель 1.5 З кількісними знижками. Для збільшення об'єму продажів компанії часто пропонують кількісні знижки своїм покупцям. Кількісна знижка – скорочена ціна на товар у разі покупки великої кількості цього товару. Типові приклади кількісних знижок подані у табл. 4.1. Таблиця 4.1
Нехай I – частка витрат зберігання в ціні продукту з. Тоді:
оптимальний розмір замовлення
Приклад 2. Розглянемо приклад, що пояснює принцип ухвалення рішення в умовах знижки. Магазин "Ведмежа" продає іграшкові гоночні машинки. Ця фірма має таблицю знижок на машинки у разі покупок їх в певній кількості (табл. 6.1). Витрати замовлення складають 49 тис. у.о. Річний попит на машинки рівний 5000. Річні витрати зберігання у відношенні до ціни складають 20%, або 0,2. Необхідно знайти розмір замовлення, що мінімізує загальні витрати. Розв’язання: Розрахуємо оптимальний розмір замовлення для кожного виду знижок, тобто Q1*, Q2* і Q3*, і одержимо Q1* = 700; Q2* = 714; Q3*=718. Оскільки Q1* – величина між 0 і 999, то її можна залишити колишньою. Q2* менше кількості, необхідного для отримання знижки, отже, його значення необхідно прийняти рівним 1000 одиниць. Аналогічно Q3* беремо рівним 2000 одиниць. Одержимо Q1* = 700; Q2* = 1000; Q3* = 2000. Далі необхідно розрахувати загальні витрати для кожного розміру замовлення і виду знижок, а потім вибрати якнайменше значення.
Розглянемо наступну таблицю.
Виберемо той розмір замовлення, який мінімізує загальні річні витрати. З таблиці видно, що замовлення у розмірі 1000 іграшкових гоночних машинок мінімізуватиме сукупні витрати.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 313; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.011 с.) |


 ;
; ;
;




 ;
; ;
;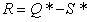 .
.

 ;
; ;
; ;
; ;
; .
. ;
; .
.


