Приклад постановки задачі лінійного програмування

Акціонерне товариство виготовляє і реалізує оптовими партіями відповідно за ціною 45 грн. і 30 грн. книги й настільні календарі. Постійні витрати суспільства (управлінські витрати, зміст офісу й т.п.) становлять 202200 грн. у квартал, змінні витрати (вартість паперу, послуги друкарні й т.п.) – відповідно 15.75 грн. і 12.3 грн. розраховуючи на одну книгу й один календар. Податок на додану вартість становить 16.67 % ціни виробу.

Досвід реалізації виробів у попередні планові періоди показав, що протягом кварталу можна реалізувати не більше 100000 книг і 40000 календарів.

Потрібно на планований квартал визначити обсяг виробництва й реалізації виробів (структуру виробництва й реалізації), при якому суспільство дістане максимальний прибуток, а сумарні витрати на виробництво й реалізацію виробів не будуть перевершувати грн руб.

Формування математичної моделі

Позначимо через х1(х2) невідомий обсяг виробництва й реалізації книг (календарів). Сумарні витрати Z на виробництво й реалізацію виробів можна виразити у вигляді функції невідомих об'ємів реалізації виробів:

Z(x₁,x₂)=202200+15.75x₁+12.3x₂. (1.1)

Очікувана сума виторгу суспільства V, розглянута як функція невідомих обсягів виробництва й реалізації, складе:

V(x₁,x₂)=45x₁+30x₂. (1.2)

Сума податку на додану вартість N також виражається у вигляді функції невідомих об'ємів реалізації:

N(x₁,x₂)=0.1667*(45x₁+30x₂)=7.5x₁+5x₂. (1.3)

Прибуток акціонерного товариства P можна записати у вигляді функції невідомих об'ємів x₁ і x₂ у такий спосіб:

P(x₁,x₂)=V(x₁,x₂)-Z(x₁,x₂)-N(x₁,x₂) = 45x₁+30x 2-₂₀₂₂₀₀ –157.5x 1-₁₂₃x₂-7.5x 1-₅x₂==21.75x₁+12.7x 2-202200. (1.4)

Таким чином, математична модель ситуації записується в такий спосіб:

21.75x₁+12.7x 2-₂₀₂₂₀₀®max, (1.5)

202200+15.75x₁+12.3x₂£2000000, (1.6)

0 £ x₁ £ 100000, 0 £ x₂ £ 40000. (1.7 )

Модель (1.5)-(1.7) можна записати в наступному видгляді:

21.75x₁+12.7x₂®max, (1.8)

15.75x₁+12.3x₂£1797800, (1.9)

x₁ £ 100000, (1.10)

x₂ £ 40000, (1.11)

x₁ ³ 0, x₂ ³ 0. (1.12)

 

2. Введення умов задачі:

2.1.
Сформувати таблицю в діапазоні середовищ A1:F11, наведену на рис. 1

 

Рис. 1. Таблиця для введення умов задачі лінійного програмування

2.2. В осередок D6 ввести формулу =СУММПРОИЗВ(B$3:C$3;B6:C6).

2.3. В осередок D9 ввести формулу =СУММПРОИЗВ(B$3:C$3;B9:C9) і розмножити по стовпці в осередках D10 і D11.

Розв’язання задачі

3.1. У меню вибрати «Сервіс - Пошук розв’язку». У поле «Встановити цільове середовище:» набрати $D$6. У поле «Рівної:» установити маркер в «Максимальному значенню».

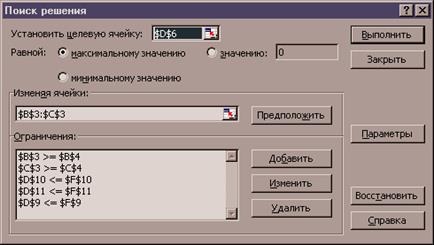
3.2. В поле «Змінюючи середовище» ввести $B$3:$C$3.

3.3. Встановити курсор-прямокутник в поле «Обмеження». Натиснути на кнопку «Додати». У поле «Посилання на осередок:» ввести $B$3. Вибрати знак >=. В поле «Обмеження» ввести =$B$4. Нажати кнопку «Додати».

3.4. В поле «Посилання на середовище:» ввести $З$3. Вибрати знак >=. В поле «Обмеження» ввести =$З$4. Натиснути кнопку «Додати».

3.5. В поле «Посилання на середовище:» ввести $D$9. Вибрати знак <=. В поле «Обмеження» ввести =$F$9. Натиснути кнопку «Додати»

3.6. В поле «Посилання на середовище:» ввести $D$10. Вибрати знак <=. В поле «Обмеження» увести =$F$10. Нажати кнопку «Додати»

3.7. В поле «Посилання на середовище:» ввести $D$11. Вибрати знак <=. В поле «Обмеження» ввести =$F$11. Нажати кнопку OK. У результаті діалогове вікно Пошук розв’язку повинне бути заповнене також як на рис. 2.

Рис. 2. Діалогове вікно Пошук розв’язку

Натиснути кнопку «Параметри». Установити лінійну модель. Натиснути

Кнопку OK. Нажати кнопку «Виконати».

У діалоговому вікні «Результати пошуку розв’язку», наведеному на мал. 3, установити маркер на опцію «Зберегти знайдений розв’язок» і вибрати у вікні «Тип звіту – Результати». Натиснути OK.

Рис. 3. Діалогове вікно Результати пошуку розв’язку

3.10. В таблиці з'являться вихідні значення, наведені на рис. 4.

	Товари
ім'я	Книги(х1)	Календарі(х2)
значення
нижня границя
верхня границя			ЦФ	напр
коеф. у ЦФ	21,75	12,70		макс.
	Обмеження
вид			ліва частина	знак	права частина
b1	15,75	12,30		<=	1797800,00
b2	1,00	0,00		<=	100000,00
b3	0,00	1,00		<=	40000,00

Рис. 4. Вихідна таблиця розв’язку задачі лінійного програмування

Завдання до роботи

Зробити регресійний аналіз даних, проаналізувати вплив початкових даних на оцінні коефіцієнти регресійної моделі, і при необхідності перерахувати її. Розв’язати задачу лінійного програмування засобами Excel.

Порядок виконання роботи

1). Проведення регресійного аналізу:

– Створити аркуш з ім'ям «Регресійний аналіз»;

– Вибрати собі з пункту «Варіанти завдання до роботи» завдання для проведення регресійного аналізу. Номер свого варіанту дізнатись у викладача;

– Зробити математичне формулювання задачі у вигляді таблиці вихідних даних. Вибір вихідних даних відбувається по всіх рядках таблиці «Дані для проведення регресійного аналізу», а стовпці вибираються по таблиці «Регресійний аналіз» відповідно до номера свого варіанта;

– Запустити пакет регресійного аналізу через меню «Сервіс - Пакет аналізу – Регресія».

– У вікні «Регресія» задати інтервали, що містять Y і X. Результати обробки розташувати на аркуші «Регресійний аналіз»;

– Проаналізувати значення t-статистики для кожного коефіцієнта моделі. Якщо яке-небудь значення не перевищує за абсолютним значенням граничного значення 3, то відповідний фактор X варто вважати не впливає істотно на Y, виключити його з подальшої обробки й повторити «Регресійний аналіз».

2). Рішення задачі лінійного програмування (ЗЛП):

– Вибрати задачу лінійного програмування відповідно до свого варіанта з розділу «Задачі лінійного програмування» пункту «Варіанти завдань до роботи»;

– Створити новий аркуш із ім'ям «РЗЛП»

– На знову створеному аркуші зробити математичне формулювання ЗЛП у вигляді таблиць вихідних даних;

– Відкрити вікно пошуку рішень через меню «Сервіс - Пошук рішення...».

– Вирішити ЗЛП для свого варіанта, на основі послідовності, наведеної в прикладі, описаному в пункті «Методика виконання роботи». Вихідні дані й результат розмістити на аркуші «РЗЛП».

3). Доповісти викладачеві про закінчення виконання роботи;

Вимога до захисту роботи

1). Звіт про виконання лабораторної роботи;

2). Конспект порядку виконання лабораторної роботи.

3). Знати відповіді на ВСІ контрольні питання.

Зміст звіту

1). Назва й мета лабораторної роботи;

2). Вміст аркуша «Регресійний аналіз», створеного в П.1 «Порядку виконання роботи».

3). Вміст аркуша «РЗЛП », створеного в П.2;

4). Вміст автоматично створеного аркуша «Звіт за результатами 1» з результатами рішення ЗЛП;

5). Висновки.

Контрольні питання

1. Які засоби для побудови математичних моделей і прогнозування стану об’єкта що моделюється містить Excel?

2. Яке призначення регресійного аналізу?

3. Що таке рівняння регресії?

4. Які види регресії розрізняють? Наведіть приклади?

5. Що показує коефіцієнт множинної кореляції Пірсона?

6. У чому полягає задача побудови регресійної залежності?

7. Для чого застосовується F-Критерій Фішера? Як він обчислюється?

8. Якими параметрами визначається значимість коефіцієнта Пірсона?

9. Як побудувати лінійну регресійну модель в Excel?

10. Що характеризує t-статистика?

11. Яка технологія побудови регресійної моделі?

12. Яке призначення програми-надбудови "Пошук рішення"?

13. Яка загальне формулювання задачі лінійного програмування?

14. У чому полягає економічний зміст задачі лінійного програмування?

15. Як буде сформульована задача лінійного програмування для розглянутого приклада задачі про раціональну годівлю тварин?

16. Як оформити у вигляді таблиці, що відбиває основні залежності, математичне формулювання задачі лінійного програмування?

17. Який зміст комірок таблиці, підготовленої для пошуку розв’язку?

18. Як завантажити програму пошуку рішення задачі лінійного програмування?

19. Які параметри варто встановити у вікні "Пошук розв’язку "?

20. Як інтерпретувати отримані результати розв’язок задачі лінійного програмування?

Література

1). Зайден М. Excel 2000 / Зайден М.; Науч. ред.: А. Плещ, С. Молявко. - М.: Лабораторія Базових Знань, 2000 - 336 с.: іл. + табл.. - (Комп'ютер)

2). Вейсскопф Д. Excel 2000. Базовий курс (русифікована версія) / Вейсскопф Д.; Пер. с англ. під ред. В.В. Легейды, Б.Г. Жадаева. - Київ - М.- Спб.: СТОЛІТТЯ+; ЭНТРОП; Корона-Принт, 2000 - 400 с.: іл. + табл.. - Слів. термінів Excel: с. 377-384.-Предметний указ.: с. 385-393

3). Саймон Д. Аналіз даних в Excel = Excel Data Fnalysis: Наочний курс створення звітів, діаграм і вільних таблиць / Саймон Д.; Пер. с англ. И.В. Константинова; Під ред. И.В. Василенко. - М.- Спб.- Київ: Діалектика, 2004 - 517 с.: іл. + CD-ROM. - (Читаючи менше, дізнавайся більше!). - Прил.: с. 471-511.-Предметний указ.: с. 512-516

4). Лавренов С.М. Excel: Збірник прикладів і задач / Лавренов С.М.; Рец.: О.А. Козлов, Р.А. Подбельская. - М.: Фінанси й статистика, 2003 - 336 с.: іл.. - (Діалог з комп'ютером). - Библиогр.: с. 304-306.-Прил.: с. 307-332